Wydział WNiG	Michał Kubik Jakub Molęda Łukasz Czerwik	Rok II	Grupa 2	Zespół 2/1
	Temat : Wyznaczanie współczynnika oporu skupionego ξ = f(Re) jako funkcja liczby Reynoldsa			Nr ćwiczenia 5

Cel ćwiczenia

Celem ćwiczenia jest doświadczalne wyznaczenie bezwymiarowego współczynnika oporu lokalnego ξ. Przedmiotem pomiarów jest nagłe przewężenie przewodu o stałej średnicy.

Wprowadzenie

Podczas przepływu płynu występują straty ciśnienia na oporach zwanych lokalnymi lub miejscowymi. Na oporach lokalnych następują zmiany kierunków oraz modułów wektorów prędkości. Zawirowania powodują straty energii większe od tych, które występują podczas przepływu przez odcinek prostoliniowy

Wielkość straty ciśnienia na oporze lokalnym wynosi:

Gdzie:

ξ - bezwymiarowy współczynnik oporu lokalnego odniesiony zazwyczaj do prędkości za przeszkodą

v - średnia prędkość w przekroju odniesienia.

Wartość współczynnika ξ określa się eksperymentalnie. Wielkość ξ zależy od kształtu elementu wywołującego opór, prędkości przepływu, gęstości i lepkości płynu. Przy przepływie laminarnym współczynnik ξ maleje ze wzrostem liczby Reynoldsa, natomiast przy w pełni rozwiniętym przepływie turbulentnym ma wartość stałą.

Rozważa się przepływ płynu o gęstości ρ przez poziome połączone ze sobą szeregowo przewody kołowe

Między przewodami 1 i 2 znajduje się opór lokalny. Starta ciśnienia na rozważanym odcinku jest sumą strat liniowych oraz straty na oporze lokalnym. Strata ciśnienia na oporze liniowym jest równa:

Strata ciśnienia na oporze lokalnym wynosi

Dane:

l₁=170 mm

l₂=200 mm

l₃=495 mm

l₄=395 mm

ρ_pow=1.155 kg/m³ dla temp. mokrej t=13,6 °C i temp. suchej t=21 °C

ρ_c=800 kg/m³ - gęstość cieczy w U-rurkach.

ν=16⋅10^-6 m²/s

Korzystamy ze wzorów:

Bezwymiarowy współczynnik oporu liniowego obliczamy wg wzoru

Prędkość średnią obliczamy wg wzoru

Różnice ciśnień w U-rurce pierwszej obliczamy wg wzoru

W U-rurce drugiej

Gdzie: Δh - różnica poziomów w U-rurkach

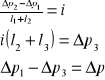
Dla d=26 mm	v [m/s]	Δp1 [Pa]	Δp2 [Pa]	i[N/m^3]	Δp3 [Pa]	Δp [Pa]	Re	ξ
		6,4	47,088	54,936	21,21	14,74	32,35	10400	1,37
		7,7	62,784	86,328	63,63	44,22	18,56	12510	0,54
		9,3	86,328	117,72	84,84	58,96	27,37	15110	0,55
		11	117,72	172,656	148,48	103,19	27,37	17880	0,21
		13	156,96	235,44	212,11	147,42	9,54	21120	0,1
		15,2	211,896	313,92	275,74	191,64	20,26	24700	0,15

Dla d=20 mm	v [m/s]	Δp1 [Pa]	Δp2 [Pa]	i[N/m^3]	Δp3 [Pa]	Δp [Pa]	Re	ξ
		7,6	125,57	164,81	69,45	48,27	77,3	12350	2,32
		9,4	204,05	243,29	69,45	48,27	155,78	15280	3,05
		11,58	306,07	368,87	111,15	77,25	228,82	18820	2,95
		13,56	415,94	502,27	152,79	106,19	309,75	22040	2,91
		14,92	502,27	604,29	180,57	125,5	376,77	24250	2,93
		16,21	596,45	714017	208,35	144,8	451,65	26340	2,97

Dla d=15 mm	v [m/s]	Δp1 [Pa]	Δp2 [Pa]	i[N/m^3]	Δp3 [Pa]	Δp [Pa]	Re	ξ
		5	219,74	235,44	27,79	19,31	200,43	3750	13,88
		6	329,62	353,16	41,66	28,94	300,68	4500	14,46
		7	455,18	486,58	55,57	38,62	416,56	5250	14,72
		7,9	549,36	588,6	69,45	48,27	501,09	5925	13,9
		8,9	722,02	761,26	69,45	48,27	673,75	6675	14,73
		9,9	878,98	941,76	111,11	77,22	801,76	7425	14,16

Dla d=12 mm	v [m/s]	Δp1 [Pa]	Δp2 [Pa]	i[N/m^3]	Δp3 [Pa]	Δp [Pa]	Re	ξ
		3,6	164,81	172,66	13,89	9,65	155,16	2700	20,73
		4,9	313,92	321,77	13,89	9,65	304,27	3675	21,94
		6,2	486,58	510,12	23,54	16,36	470,22	4650	21,18
		7,1	651,38	674,93	41,68	28,97	622,41	5325	21,38
		7,9	816,19	863,28	83,34	57,92	758,27	5925	21,04
		9,2	1079	1130	90,26	62,73	1016,27	6900	20,79

Wnioski:

Po przeprowadzonym oświadczeniu możemy stwierdzić, że mamy do czynienia z przepływem turbulentnym, gdyż współczynnik oporu skupionego ξ zmienia się nieznacznie, choć liczba Reynoldsa wzrasta.

---