Uniwersytet Zielonogórski

Wydział Inżynierii Lądowej i Środowiska,

Zakład Sieci i urządzeń sanitarnych

MECHANIKA PŁYNÓW

LABORATORIUM

Sprawozdanie z ćwiczenia laboratoryjnego nr 7.

„Charakterystyka kryzy”

GRUPA 29 ISMD

( poniedziałek, g. 11.15 - 13.00 )

w składzie:

1. Darek Kobiela

2. Dagmara Kwaśniewska

3. Katarzyna Sterna

Data odbycia zajęć:

08.12.2003 r.

Data oddania sprawozdania:

15.12.2003 r.

OCENA:

1. Cel ćwiczenia.

Celem ćwiczenia jest poznanie zasady mierniczej zwężek oraz wyznaczenie współczynnika przepływu zwężki pomiarowej w zależności oj liczby Reynoldsa.

2. Zakres wymaganych wiadomości..

Zwężką pomiarową nazywamy przegrodę z otworem, zazwyczaj współśrodkowym, mniejszym od przekroju przewodu, w którym przegroda została wbudowana w celu wywołania spadku ciśnień. Zwężki pomiarowe dzielimy na trzy zasadnicze grupy:

• kryzy,

• dysze,

• zwężki Venturiego.

W kryzach przepływająca struga odrywa się od krawędzi wlotowej, w dyszach - płynie wzdłuż jej powierchni wewnętrznej, po czym odrywa się od niej przy wylocie z części cylindrycznej, a w zwężkach jest ograniczona elementami zwężki na całej długości. Te zasadnicze różnice w przebiegu strug wywierają decydujący wpływ na charakter zjawiska ruchu płynu, a zwłaszcza na wielkość strat energetycznych.

Przebieg zjawisk hydromechanicznych w zwężce.

Wskutek nagłego zmniejszenia się przekroju przepływowego w kryzie lub stopniowego w dyszy i zwężce przy przejście z przekroju przewodu do przekroju przewężenia następuje wzrost średniej prędkości przepływu, a tym samym zmniejszenie ciśnienia. W przekroju A-A pojawia się wpływ kryzy na strugę, jej przekrój zaczyna się zmniejszać, a średnia prędkość odpowiednio wzrasta. Wskutek bezwładności struga zwęża się na pewnym odcinku za kryzą. Dlatego miejsce największego zwężenia strugi znajduje się w przekroju B-

Odległość przekroju A-A od kryzy jest nie większa niż średnica przewodu D, a odległość przekroju B-B w przybliżeniu równa 0,5 D.

Na odcinku A-A do B-B średnia prędkość wzrasta od v_A do v_B. Przy ścianie przewodu, przed i za kryzą powstają wiry (są one większe po stronie odpływu). Odpowiednio wzrasta również energia kinetyczna. Wzrost ten może odbywać się tylko w wyniku zmniejszania energii potencjalnej, a co za tym idzie ciśnienia - od p_A do p_B. Najmniejszą wartość ciśnienia uzyskuje się w miejscu gdzie strumień jest najwęższy. Następnie struga zaczyna stopniowo rozszerzać się i w przekroju C-C osiąga ścianki przewodu. Proces ten charakteryzuje się stopniowym zmniejszaniem prędkości i wzrostem ciśnienia. W przekroju C-C prędkość v_C będzie równa prędkości v_A, jeśli gęstość płynu nie zmieni się, natomiast ciśnienie p_C będzie mniejsze od ciśnienia p_A wskutek znacznych strat energii w martwych strefach znajdujących się za kryzą.

Przepływająca z dużą prędkością struga porywa płyn z martwych stref, co wywołuje częściowy przepływ powrotny płynu do przekroju C-C do kryzy wzdłuż ścianek przewodu. W martwych strefach powstają silne zawirowania i straty energii. Wartość ostatecznej straty ciśnienia (p_A-p_C) wynosi dla kryz od 40 do 90% spadku ciśnienia (p_A-p_B), zmniejszając się wzrostem względnej średnicy kryzy d/D. Należy zaznaczyć, że bezpośrednio w kryzie straty energii wywołane tarciem i zwężeniem wynoszą nie więcej niż 2% spadku (p_A-p_B).

Zależność między natężeniem przepływu a spadkiem ciśnienia, który w ogólnym przypadku nie musi być mierzony w przekrojach A-A i B-B, można otrzymać z równoczesnego rozwiązania uogólnionego równania Bernoulliego dla przewodu poziomego:

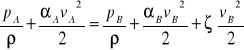
(1)

i równania:

(2)

w których:

α_A i α_B - współczynniki Coriolisa (energii kinetycznej) w przekrojach A-A i B-

ζ - współczynnik straty na odcinku A-B odniesiony do prędkości v_B,

A_A i A_B - pole przekrojów A-A i B-B strugi.

Stosunek pola najmniejszego przekroju strugi A_B do pola otworu kryzy A₀ nazywamy współczynnikiem kontrakcji (zwężenia) strugi i oznaczamy na ogół przez x, zatem:

(3)

współczynnik x określa stopień dodatkowego zwężenia strugi pod wpływem sił bezwładności po przejściu przez otwór. Dla kryzy x wynosi 0,6 - 0,78, dla dyszy ≈ 1,0.

Stosunek pola otworu A₀ do pola przekroju poprzecznego przewodu nazywamy modułem zwężki i oznaczamy literą m, tak więc:

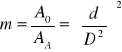
(4)

Po podstawieniu wzoru (3) i (4) do równania (2) otrzymamy :

(5)

Rozwiązując następnie równanie (1) względem v_B z uwzględnieniem (5) i fakt, że punkty odbioru ciśnienia p₁ przed i p₂ za kryzą nie muszą w ogólnym przypadku pokrywać się z przekrojami A-A i B-B, otrzymamy:

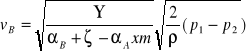
, (6)

przy czym:
.

Strumień objętości jest więc określony zależnością:

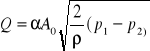
, (7)

w której

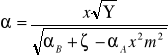
(8)

Wielkość α nazywamy współczynnikiem przepływu zwężki. Jak wynika z zależności (8), uwzględnia o wpływ następujących czynników:

1. nierówności rozkładu prędkości w przewodzie i zwężaniu strugi (α_A i α_B) ,

2. stopnie zwężenia strugi ( m i x).

3. strat (ζ) ,

4. usytuowanie punktów odbioru ciśnienia (Y).

Trzy z wymienionych czynników: nierównomierność rozkładu prędkości, stopień zwężenia strugi i straty zależą od liczby Reynoldsa:

.

Współczynnik α można zatem przedstawić jako funkcję Y, m i Re, a dla określonego sposobu odbioru ciśnienia tylko jako funkcję m i Re.

Ponieważ zależności α_AB = f(Re), x = f(Re) i ζ = f(Re) są różne dla różnych zwężek, więc zależności od tego, który z podanych czynników ma największe znaczenie dla zwężki rozpatrywanego rodzaju, współczynnik przepływu ze wzrostem liczby Reynoldsa może rosnąć ( np. dysza) lub maleć (np. kryza). Zmiana ta występuje jednak tylko do określonej wartości Re =Re', powyżej której współczynnik przepływu prawie się nie zmienia.

Aby wyznaczyć współczynnik przepływu α, przeprowadzono wiele eksperymentów. Uogólnione zależności otrzymano dzięki teorii podobieństwa. Z warunków podobieństwa wynika bowiem, że współczynniki przepływu dwóch zwężek będą takie same, jeśli będzie spełniony:

1. warunek podobieństwa geometrycznego, tzn. podobny będzie ich kształt, a ich względne średnice d₁/D₁ i d₂/D₂ lub moduły m₁ i m₂ będą sobie równe.

2. warunek podobieństwa hydromechanicznego (dwie strugi są podobne, jeśli są równe ich liczby Reynoldsa).

3. Schemat stanowiska.

4. Opis przebiegu doświadczenia.

Włączamy pompę, która spowoduje obieg wody w układzie. Następnie w rotametrze zmieniamy położenie pływaka, zmieniając przepływ wody. Zmiana przepływu powoduje spadek poziomu cieczy w poszczególnych piezometrach. Odczytujemy wysokości cieczy w obu piezometrach, a wyniki zapisujemy w tabeli. Po wykonaniu 26 pomiarów wyłączamy urządzenie.

5. Tabela pomiarowa.

Lp.	V		h1	h2	p1-p2	U	Re	α
		l/h	m^3/s	mm	mm	N/m^2	m/s
1	5	1,39*10^-6	969	966	29,42	2,76*10^-2	169,8	1,82
2	6	1,67*10^-6	967	964	29,42	3,32*10^-6	204,3	2,19
3	7	1,94*10^-6	966	960	58,84	3,86*10^-2	237,5	1,8
4	8	2,22*10^-6	964	955	88,26	4,42*10^-2	272	1,7
5	9	2,5*10^-6	963	952	107,88	4,97*10^-2	305,8	1,7
6	10	2,78*10^-6	954	939	147,1	5,53*10^-2	340,3	1,6
7	11	3,06*10^-6	957	935	215,8	6,09*10^-2	374,8	1,5
8	12	3,33*10^-6	955	921	333,4	6,62*10^-2	407,4	1,3
9	13	3,61*10^-6	952	909	421,7	7,18*10^-2	441,8	1,2
10	14	3,89*10^-6	950	894	549,2	7,74*10^-2	476,3	1,2
11	15	4,17*10^-6	946	875	696,3	8,3*10^-2	510,8	1.1
12	16	4,44*10^-6	943	860	814	8,83*10^-2	543,4	1,1
13	17	4,72*10^-6	939	841	961,1	9,39*10^-2	577,8	1,1
14	18	5*10^-6	936	821	1127,8	9,95*10^-2	612,3	1,4
15	19	5,28*10^-6	931	800	1284,7	0,105	646,2	1,5
16	20	5,56*10^-6	925	770	1520,1	0,11	683,1	1,5
17	21	5,83*10^-6	923	749	1706,4	0,12	713,8	1,6
18	22	6,11*10^-6	917	720	1932	0,12	750,8	1,6
19	23	6,39*10^-6	914	695	2147,7	0,13	781,5	1,63
20	24	6,67*10^-6	909	669	2353,7	0,13	818,5	1,7
21	25	6,94*10^-6	905	639	2608,7	0,14	849,2	1,7
22	26	7,22*10^-6	902	612	2844	0,14	886,2	1,73
23	27	7,2*10^-6	894	573	3148,1	0,15	917	1,76
24	28	7,7810^-6	889	545	3373,6	0,16	953,8	1,8
25	29	8.0610^-6	885	510	3677,6	0,16	984,6	1,83
26	30	8,3310^-6	878	466	440,5	0,17	1021,5	1,85

6. Przykładowe obliczenia.

- zamiana jednostek wydatku objętościowego z dm³/h na m³/s:

-

-obliczanie prędkości przepływu:

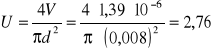
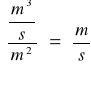
-obliczanie liczby Reynoldsa:

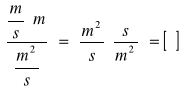
- obliczanie współczynnika Coriolisa:

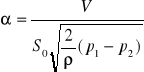
gdzie:

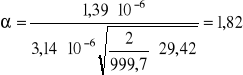
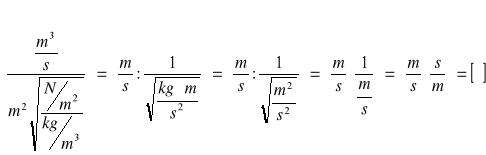
7. Wykresy.

8. Wnioski i obserwacje.

Na podstawie wykonanego doświadczenia wnioskujemy, iż po przepływie cieczy przez kryzę następuje spadek ciśnienia. Wraz ze spadkiem ciśnienia oraz po przepływie cieczy przez kryzę wzrasta prędkość przepływu. Wraz ze wzrostem zwiększanego przez nas przepływu wzrasta również wydatek objętościowy i liczba Reynoldsa. Obserwujemy, że wraz ze zwiększonym przepływem ciśnienie za kryzą zmniejsza się.

---