1. Wskaż filtr który nie posiada biegunów
(jednokrotnego wyboru)
FIR <-

2 Zaznacz filtry które posiadają bieguny
(wielokrotnego wyboru)
IIR <-
Butterwortha <-
Czebyszewa <-

3 Wskaż poprawną definicję równania różnicowego
(jednokrotnego wyboru)

4. Czym mogą się różnić struktury filtrów cyfrowych
(wielokrotnego wyboru)

ilością bloków sumujących <-
ilością bloków opóźniających <-
ilością bloków mnożących <-

5. Wzór na transmitancję filtru cyfrowego.

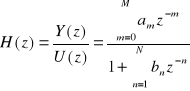
6. W transformacji (...) "z" jest:

Liczbą zespoloną

7. Transformata Fouriera jest równa transformacji Z gdy: ... ?

8. Co to jest filtr minimalnofazowy?

Filtr minimalnofazowy to taki, którego wszystkie zera znajdują się wewnątrz okręgu jednostkowego.

9. Tłumienie.

Istotnym parametrem filtru jest tłumienie (lub wzmocnienie) dla częstotliwości przenoszonych (pasmo przenoszenia) oraz maksymalne tłumienie dla częstotliwości nieprzenoszonych (pasmo zaporowe).

10. Co to jest filtr eliptyczny?

Charakteryzuje się dużą nieliniowością charakterystyki fazowej oraz dużą stromością nachylenia charakterystyki. W paśmie przepustowym jak i zaporowym występują tętnienia. Filtr Eliptyczny można stosować tylko tam, gdzie faza nie stanowi istotnego parametru projektowego.

11. Warunek stabilności filtru IIR
- zera w kole jednostkowym;

12. Przyjmujemy, że t - to czas dyskretny wówczas transformata Z ma postać:

13. Zera mają sprzężone współrzędne: z= +/- j. Dla jakich współrzędnych biegunów filtr jest stabilny (1 z 4).

?

14. Pytanie czym charakteryzuj się filtr Butterwortha (1 z 4) (dotyczyło to pasm - tzn. jakie dane pasmo jest dla tego filtra np.: strome zaporowe, czy przejściowe <- podpunktów nie pamiętam).

Filtr Butterwortha charakteryzuje się płaskim pasmem przepustowym, nieliniowością charakterystyki fazowej oraz małą stromością charakterystyki, którą można zwiększyć zwiększając rząd filtru co jednak radykalnie zwiększa ilość obliczeń

15. Było jeszcze pytanie związane ogólnie z pasmami filtrów -   które powinno być jakie aby filtr był jak najbardziej zaporowy (czy coś takiego).

Idealny filtr zaporowy posiada zerową tłumienność w paśmie przenoszenia, idealną stromość zboczy (90 stopni) i nieskończenie wielkie tłumienie w paśmie zaporowym. Wykres tłumienia (T) w funkcji częstotliwości wyglądałby tak:

17. Schematu przepływu sygnału przez filtr:

18. Splot dyskretny:

19. Cos z długością pasma przejściowego w filtrze cyfrowym (chyba dlaczego nie może być nieskończenie krótkie).

Dlatego, iż w rzeczywistym filtrze zmiana wzmocnienia między pasmem przepustowym a

zaporowym nie będzie skokowa lecz będzie wymagać skończonego niezerowego czasu

trwania.

20. Był podany filtr jakiegoś kolesia i miałem podać czym on się charakteryzuje.

Filtr Czebyszewa charakteryzuje się tętnieniami pasma przepustowego oraz zaporowego, nieliniowością charakterystyki fazowej i większą w porównaniu z filtrem Butterwortha stromością charakterystyki.

21. Wzór na transformatę Z.

22. W jakim paśmie używa sie filtra FIR? (?)

23. Jakie są cechy filtra IIR?

Filtry rekursywne o nieskończonej odpowiedzi impulsowej (NOI) (ang. infinite impulse response IIR). Są to filtry w strukturze których występuje pętla sprzężenia zwrotnego, każda próbka odpowiedzi zależy od poprzednich .W rezultacie odpowiedź impulsowa dowolnego filtru rekursywnego może mieć nieskończoną liczbę próbek. Filtry te charakteryzują się lepszymi charakterystykami amplitudowymi przy niższych rzędzie filtru niż filtry SOI.

24. Metoda tworzenia FIR.

Ewolucyjne projektowanie filtrów cyfrowych FIR ?

25. Wzór na zera i bieguny.

26. Cechy FIR.

Nazwa FIR oznacza filtr o skończonej odpowiedzi impulsowej (polski skrót tej nazwy to filtr SOI). Oznacza to tyle, że reakcja na wyjściu tego układu na pobudzenie o skończonej długości jest również skończona (przez długość pobudzenia i odpowiedzi rozumiemy tu długość odcinka czasu, dla którego próbki sygnału przyjmują wartości niezerowe). Aby warunek ten był spełniony, w filtrach tego typu nie występuje pętla sprzężenia zwrotnego, co widać na poniższym schemacie (porównaj z filtrem NOI, w którym występuje pętla sprzężenia zwrotnego).

27. Na czym polega obecnie optymalizacja działania filtrów?

Minimalizowanie złożoności obliczeniowej.

---