Zad.1 Michalina zmieszała 2/3 szklanki soku  pomarańczowego i 1/3 soku cytrynowego. Wypiła pół szklanki napoju ale jej jeszcze nie smakował, więc dopełniała ją sokiem cytrynowym. Potem wypiła 1/3  napoju i dopełniła go sokiem pomarańczowym. Następnie wypiła 1/6 szklanki  napoju ale jeszcze jej nie smakował więc dopełniła szklankę sokiem cytrynowym.  Napój okazał się wspaniały. Michalina wypiła go aż do dna. Ile szklanek napoju  wypiła Michalina i którego soku wypiła więcej, cytrynowego, czy pomarańczowego?

Zad. 2 Sad owocowy ma kształt prostokąta, którego długości boków są
w stosunku 2 : 7. Krótszy bok ma 240 metrów. W ciągu ilu dni obejdzie ten sad dookoła ślimak idący ze średnią prędkością 4 m/godz.?

Zad. 3 Bartosz wyjechał na deskorolce na spotkanie z Patrykiem.
W ciągu 8 minut przejechał 3,2 km, a następnie zwiększył swoją
prędkość o 1/5 prędkości dotychczasowej i do spotkania jechał jeszcze
8 minut. Oblicz, jaką drogę przebył Bartosz i z jaką prędkością jechał na deskorolce.

Zad.4 Podaj 2003 cyfrę rozwinięcia dziesiętnego ułamka
.

Zad.5 Liczba monet w kolekcji jest większa od 300, a mniejsza od 350, przy dzieleniu przez 15 daje resztę 9, a przy dzieleniu przez 8 - resztę 4. Ile monet jest w tej kolekcji?

Zad. 6 Prostokąt podzielono na cztery części, tak jak pokazano.
Podano pola trzech z tych części. Ile wynosi pole całego prostokąta?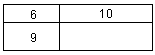

Zad. 7 Liczba naturalna nazywa się dobrą jeśli zapisana jest przy pomocy różnych cyfr i iloczyn tych cyfr równy jest 360. Podaj co najmniej dwie takie liczby naturalne. Wyznacz największą dobrą liczbę naturalną.

Zad. 8 Bak był pełen wody. Wodę z baku przelano do trzech pojemników. Do każdego z nich przelano tę samą całkowitą liczbę litrów wody. Okazało się, że w pierwszym pojemniku woda wypełniła 1/2 jego objętości, w drugim 2/3, zaś w trzecim 3/4. Przy jakiej najmniejszej objętości baku jest możliwa taka sytuacja, jeśli objętość baku i pojemników wrażają się liczbami całkowitymi.

Zad. 9 Cenę butów obniżono o 15%, a potem podwyższono o 10% i 2 złote. Obecnie cena butów wynosi 39,4 złotych. Jaka była cena butów przed obniżką, a jaka po obniżce?

Zad.10 Pewna liczba całkowita przy dzieleniu przez 3 daje resztę 2, zaś przy dzieleniu przez 4 daje resztę 1. Jaką resztę daje ta liczba przy dzieleniu przez 12?

Zad.11 Oblicz:

.

Zad.12 Dwie liczby zwierciadlane (jedna powstaje z drugiej, gdy ją odczytać od końca na przykład 347 oraz 743 ) pomnożono i otrzymano wynik 92565.Jakie to liczby?

Zad. 13 Dzieląc pewną liczbę naturalną przez 2, 3, 4, 5, 6, 7 otrzymujemy tę samą resztę równą 2.

1. Wyznacz najmniejszą liczbę o podanej własności większą niż 10.

2. Wyznacz najmniejszą liczbę o podanej własności, która jest ponadto podzielna przez 11.

Zad.14 Motocyklista w ciągu
godziny przejechał
zaplanowanej trasy. Jaką drogę zaplanował do przejechania motocyklista, jeżeli jechał ze średnią prędkością
km/h?

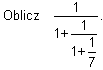
Zad. 15

Zad. 16 Znajdź ułamek o mianowniku 250 większy od 0,49, lecz mniejszy od
.

Zad.17 Staw zarasta rzęsą. Co dwa dni obszar zarośnięty rzęsą podwaja się. Cały staw zarósł rzęsą w ciągu 32 dni. Po ilu dniach ćwierć stawu było zarośnięta rzęsą?

Zad.18 Czy istnieje prostokąt, którego długości boków wynoszą odpowiednio
3/8 i 1/17 długości obwodu prostokąta?

Zad.19 Trzech chłopców ma pewną ilość monet. Pierwszy z nich dał pozostałym tyle monet ile każdy z nich posiadał. Następnie drugi,
a potem trzeci z nich postąpił tak samo, tzn. dał dwóm pozostałym tyle monet ile każdy z nich miał aktualnie. W rezultacie okazało się, że na końcu mieli po 8 monet. Ile monet posiadał każdy chłopiec na początku?

Zad. 20 W zapisie dziesiętnym liczby naturalnej wystąpiły 73 jedynki. Czy liczba ta dzieli się przez 111?

Zad. 21 W torebce jest mniej niż 100 cukierków. Ile ich jest jeśli wiadomo, że można je podzielić na 5 równych części, można je podzielić na 6 równych części, natomiast gdyby je podzielić na 7 części, to w jednej z nich będzie o 3 cukierki mniej od każdej z pozostałych.

Zad. 22 Ile razy należy dodać do siebie 8, aby otrzymać w sumie 8¹⁰⁰?

Zad. 23 Na rysunku ABCD jest kwadratem, zaś ABE trójkątem równobocznym. Jaka jest miara kąta DEC?

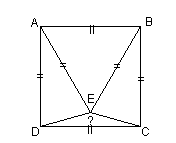
Zad. 24 Mietek przechowuje swoje oszczędności w monetach dwuzłotowych i pięciozłotowych. Dwuzłotówki stanowią 35% jego oszczędności, a pięciozłotówek ma 26. Ile ma pieniędzy?

Zad. 25 Znajdź wszystkie liczby czterocyfrowe postaci
wiedząc, że są one podzielne przez 3 i takie, że a, c, d są kolejnymi liczbami parzystymi.

(
oznacza zapis dziesiętny liczby, to znaczy: a jest cyfrą tysięcy,
b -cyfrą setek, c - cyfrą dziesiątek i d - cyfrą jedności.)

Zad. 26 Liczbę a zmniejszono o 15%, a następnie tak otrzymaną liczbę zwiększono o 15%. Czy otrzymana liczba jest większa, równa czy mniejsza od liczby a?

Zad. 27 W koszyku jest 20 grzybów. Są to prawdziwki, kozaki i podgrzybki. Ile jest w nim prawdziwków, jeśli kozaków jest 9 razy więcej niż podgrzybków?

Zad. 28 Oblicz miary kątów wewnętrznych trójkąta, jeżeli wiadomo, że jeden kąt jest 1,5 razy większy od drugiego, a trzeci jest równy sumie dwóch pozostałych kątów.

Zad. 29 Czy istnieje graniastosłup, który ma 2004 krawędzie?

Zad. 30 Do restauracji dostarczono
zamówionych produktów, dodatkowo
w południe 15% zamówionych produktów, a wieczorem 90 kg więcej niż w południe. Ile kilogramów produktów zamówiła restauracja?

Zad.31 Dwaj robotnicy sadzili drzewka. Jeden robotnik posadził, w ciągu
6 godzin pewną ilość drzewek, zaś drugi robotnik tą ilość drzewek posadził, w ciągu 5 godzin. Ile procent większa była wydajność pracy drugiego robotnika?

Zad.32

a)Wyznacz ostatnią cyfrę liczby 19⁹⁹

b) Uzasadnij, że liczba 19⁹⁹-99¹⁹ jest podzielna przez 10.

Zad. 33 Średnice okręgu o długości 6cm przecinają się pod kątem prostym. Ze środka łuku DA leżącego w punkcie E poprowadzono prostopadłe do odpowiednich średnic DB oraz AC i otrzymano na nich punkty
G oraz F. Znajdź długość odcinka GF.

Zad.34 Wypisujemy kolejne liczby naturalne w następujący sposób:
122333444455555666666...
Jaka cyfra stoi na 1999 miejscu?

Zad.35 Pięć klas ustawiło się na boisku czwórkami do marszu na wycieczkę. Wiadomo, że w każdej klasie była jedna "niepełna" czwórka. Tomek twierdził, że muszą być co najmniej dwie klasy, które mają takie same niepełne czwórki. Czy miał rację?

Zad.36Dane są dwa odcinki długości 104cm i 143cm. Znaleźć najdłuższy odcinek, który może być wspólną jednostką miary tych dwóch odcinków.

Zad.37 Woda stanowi około 90% masy grzybów. Suszono trzy kilogramy grzybów, wyparowało 8/9 wody. Ile ważą ususzone grzyby?

Zad. 38 Ułamek
napisz w postaci ułamka  łańcuchowego.

Zad.39 Zbyszek pomyślał sobie pewną liczbę. Następnie dodał do niej 5, otrzymaną sumę podzielił przez 3, a otrzymany iloraz pomnożył przez 4. Potem od ostatniego wyniku odjął 6. Gdy tę różnicę podzielił przez 7, otrzymał liczbę 2. Jaką liczbę pomyślał Zbyszek?

Zad. 40 1 stycznia 2006 roku o godzinie 12 w południe pewne dwa zegary wskazywały prawidłową godzinę. O jednym zegarze wiemy, że
w ciągu doby spieszy się o 2 minuty, a drugi w tym czasie spóźnia się o 2 minuty. Kiedy te zegary wskażą w ciągu doby tę samą godzinę? Czy będzie to w roku 2006? (na zegarze nie rozróżniamy godzin,
8⁰⁰ i 20⁰⁰ oznaczają tę samą godzinę)

---