Elektronika I rok

zestaw 15

1. Cząstka o masie m znajduje się w jednowymiarowej symetrycznej studni potencjału o nieskończenie wysokich ściankach (-a/2<x<a/2) - porównaj podobne zadanie z zestawu 14. Znaleźć wartości własne energii i unormowane funkcje własne cząstki.

2. Cząstka o masie m znajduje się w trójwymiarowej prostokątnej jamie potencjału o nieprzepuszczalnych ściankach (0<x<a, 0<y<b, 0<z<c). Złożyć, że postać przestrzennej części funkcji falowej dana jest wzorem Ψ(x,y,z)=X(x) Y(y) Z(z). Znaleźć : a) wartości własne energii i unormowane funkcje własne cząstki, b)rozpatrzyć przypadek szczególny gdy a=b=c (obliczyć różnicę energii między trzecim a czwartym poziomem, liczbę stanów odpowiadających piątemu poziomowi, liczbę stanów w przedziale (E,E+dE).

3. Cząstka o masie m i energii E pada z lewej strony na próg potencjału o wysokości U_o (rys.2). Znaleźć: a) funkcje falowe dla: x<0 oraz x>0, b) współczynnik transmisji T i współczynnik odbicia R w przypadku gdy E>U_o oraz E<U_o, c) współczynnik transmisji T i współczynnik odbicia R dla U_o<0 (gdy E>0).

4. Sprawdzić następujące reguły komutacyjne: a)
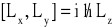
   , b*)
   ; gdzie: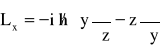
   ,
   oraz
   

5. Znaleźć wartości własne operatora
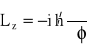
   wiedząc, że funkcja własna typu
   , spełnia warunek periodyczności tzn. :
   . Obliczyć ile wynosi stała c.

6. 
   * Możliwe wartości rzutu momentu pędu na dowolną oś są równe
   gdzie: m= -l, -l+1,...,0,...,l-1,l. Biorąc pod uwagę, że rzutu są równoprawne i równie prawdopodobne, wykazać, że w stanie z określoną wartością l średnia wartość średnia kwadratowa momentu pędu wynosi
   .

Praca pochodzi z serwisu www.e-sciagi.pl

---