1.

UKŁAD JEDNOSTEK SI. RUCH PUNKTU MATERIALNEGO. PRZYCZYNY RUCHU. 1-SZA i 2-GA ZASADA DYNAMIKI.

Układ jednostek SI:

Długość (l,s,h,r) [m] Masa (m) [kg]

Czas (t) [s] Tempera. (t,T,τ) [K]

Liczność materii (n) [mol] Natężenie prądu [A]

Światłość [cd] kąt płaski [rad]

Kąt bryłowy [sr]

Konwersja jednostek [x] = m^α * kg^β * s^γ * K^δ * mol^ϕ * A^ν * cd^ψ

Ruch - zmiana położenia ciała względem danego układu odniesienia.

Ruch prostoliniowy (jednostajny) - Jest to ruch, w którym tor jest linią prostą, a prędkość się nie zmienia.

Prędkość chwilowa równa prędkości średniej, mierzona w różnych przedziałach czasowych .

Ruchem jednostajnie zmiennym prostoliniowym - nazywamy taki ruch, w którym tor jest linią prostą, zmienia się prędkość i przyśpieszenie.

• Ruch jednostajnie przyśpieszony, kiedy prędkość rośnie a wektor i przyśpieszenie mają jednakowy zwrot.

• Ruch jednostajnie opóźniony, kiedy prędkość maleje a wektory przyśpieszenia i prędkości są przeciwne.

Ruch krzywoliniowy:

• Ruch jednostajny po okręgu - to taki ruch krzywoliniowy którego torem, jest okrąg, a wartość prędkości się nie zmienia.

Prędkość kątowa - stosunek kąta, jaki nakreśliło ciało poruszające się po okręgu, do czasu w jakim został zakreślony.

Częstotliwość:

Prędkość liniowa:

Przyśpieszenie dośrodkowe:

I zasada dynamiki - Jeżeli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym po linii prostej

to

Newton - jest to taka stała siła, która ciału o masie 1 kg nadaje przyśpieszenie 1m/s²

II zasada dynamiki - Jeżeli na ciało działa stała siła lub gdy działają siły, które się nie równoważą to ciało porusza się ruchem jednostajnie zmiennym. Przyśpieszenie jest wprost proporcjonalne do działającej siły a odwrotnie proporcjonalnie do masy ciała.

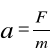
2.

ZASADY ZACHOWANIA MASY, PĘDU i ENERGII. RODZAJE SIŁ (SIŁA TARCIA i OPORU ODŚRODKA).

Zasada zachowania pędu - Jeżeli wypadkowa sił zewnętrznych jest równa 0, to całkowity wektor pędu tego ciała lub układu ciał rozważamy w inercyjnym układzie odniesienia jest stały.

Zasada zachowania energii - W przemianie energii z jednej formy w drugą całkowita ilość energii nie ulega zmianie, to znaczy jest ona zachowana.

Zasada zachowania masy - Całkowita masa relatywistyczna układu odosobnionego w którym zachodzą dowolne zjawiska fizyczne, nie zmieniają

Siła tarcia

• Siła tarcia posuwistego - występuje podczas przesuwania ciał względem siebie, przeciwstawia się ruchowi. Siła tarcia ma zawsze zwrot przeciwny do wektora prędkości ciała lub wektora siły, która to ciało wprawia w ruch.

• Tarcie kinetyczne (dynamiczne)

Fn - siła nacisku fk -współczynnik tarcia kinetycznego

• Tarcie statyczne - ciało pozostaje w spoczynku mimo działającej na nią siły.

Opór ośrodka - Siła Stokesa Siła oporu ośrodka jest wprost proporcjonalna do współczynnika lepkości ośrodka, promienia kuli i jej prędkości

Rodzaje sił

1. Siły grawitacji

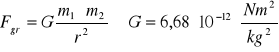
2. Elektromagnetyczne

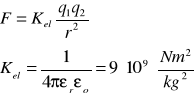
3. Bezwładność, ciężkości, Coriolisa, dośrodkowa, elektrodynamiczna i motoryczna, kolumbowska, lepkości, Lorentza, oporowa, jądrowa, między cząsteczkowa, sprężysta ………

3.

UKŁADY INERCYJNE:UJĘCIE KLASYCZNE i RELATYW. UKŁADY NIEINERCYJNE: SIŁY BEZWŁADNOŚCI (Odśr. i Coriolisa).

Siły odśrodkowe bezwładności - ruchome ciało, spoczywające w układzie obracającym się, podlega działaniu siły skierowanej wzdłuż promienia od ośrodka. Tę siłę nazywa się siłą odśrodkową bezwładności.

Siła Coriolisa :

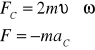
Układ inercyjny - układy odniesienia, w których jest spełniona pierwsza zasada dynamiki nazywane są układami inercyjnymi. Każdy układ odniesienia będący w spoczynku lub w ruchu jednostajnym względem dowolnego układu inercyjnego jest układem inercyjnym.

Układ nieinercyjny - To taki układ, w którym nie jest spełniona (z. d N). Jest nim każdy układ poruszający się z przyśpieszeniem np. układ związany z hamującym lub przyśpieszającym pojazdem na zakręcie.

4.

ZASADY DYNAMIKI BRYŁY SZTYWNEJ, POJĘCIA MOMENTU SIŁY i MOMENTU BEZWŁADNOŚCI, ZASADA ZACH. KRĘTU I JEJ PRAKTYCZNE ZASTOSOWANIE .

Moment siły (bryła sztywna)

Iloczyn wektorowy promienia wodzącego r_i poprowadzonego do punktu przyłożenia siły F_i przez tę siłę nazywamy momentem M_i siły F_i względem punktu 0.

Ruch obrotowy jest jednostajny wtedy, gdy wypadkowy moment względem osi obrotu wszystkich sił działających na ciało równa się zero.

Przy ruchu obrotowym działanie siły jest warunkiem koniecznym, ale nie wystarczającym do wywołania ruchu obrotowego zmiennego.

Moment bezwładności - Suma iloczynów mas poszczególnych cząstek bryły i kwadratów ich odległości od osi obrotu jest miarą bezwładności bryły w ruchu obrotowym i nosi nazwę momentu bezwładności I względem danej osi obrotu

Twierdzenie Steinera - Moment bezwładności I względem dowolnej osi jest związany z momentem bezwładności I₀ względem osi przechodzącej przez środek masy i równoległej do osi danej następującą zależnością: I = I₀ + m ⋅d ²

m - całkowita masa bryły

d - odległość wzajemna obu osi

Moment pędu (kręt) bryły - Kierunek wyznacza reguła korkociąga . Całkowity moment pędu:

Kręt bryły obracającej się dookoła nieruchomej osi równa się iloczynowi prędkości kątowej i momentu bezwładności bryły względem tej osi.

Moment siły równa się pochodnej momentu pędu względem czasu:

Zasada zachowania krętu - Jeżeli wypadkowy moment siły M_w równa się zeru, to kręt bryły pozostaje stały :

Kręt bryły może ulec zmianie jedynie pod działaniem momentu siły.

Praktycze zastosowanie - Łyżwiarka na lodzie wykonuje piruet, to rozsuwając szeroko ręce zwiększa swój moment bezwładności, a tym samym zmniejsza prędkość kątową obrotu. Jak również analogicznie. Jeżeli stojący człowiek na nieruchomym stołku obrotowym trzyma w osi pionowej koło rowerowe, które zaczyna się obracać, to stołek zacznie się przy tym obracać w przeciwnym kierunku. Wynik jest zgodny z zasadą zachowania krętu. W równoważnym układzie odosobnionym, kręt równy początkowo zeru musi zachować tę wartość. A zatem kręt koła I₁ω₁ musi być zrównoważony przciwnym co do znaku lecz równym co do wartości krętowi I₂ω₂ stołka i stojącego na nim człowieka.

5.

RUCH DRGAJĄCY: DRGANIAR HARMONICZNE, TŁUMIONE, WYMUSZONE.

Ruchem drgającym - nazywamy każdy ruch lub zmianę stanu, która charakteryzuje powtarzalność w czasie wartości wielkości fizycznych określających ten ruch lub stan.

Ruch drgający nazywamy okresowym (periodycznym) jeżeli wartość wielkości fizycznych zmieniające się podczas drgań powtarzają się w danych odstępach czasu.

Drgania harmoniczne

Drgania jakiejkolwiek wielkości fizycznej x nazywamy harmonicznymi jeżeli ich zależność od czasu t ma postać:

X = A⋅sin (ωt + ϕ₀) lub x = A⋅cos (ωt + ϕ₁)

Drgania wymuszone (rezonans)

Mają częstość taką z jaką działa siła zewnętrzna, a więc taką jaka jest częstość własna ciała. Drgania wymuszone powstają wtedy, gdy na ciało działa siła zewnętrzna okresowa. Polegają one na gwałtownym wzroście amplitudy drgań.

Drgania tłumione

Ruchem harmonicznym tłumionym nazywamy taki ruch, który odbywa się z oporami ośrodka. W takim przypadku energia maleje w czasie, zatem maleje również amplituda drgań, natomiast okres drgań pozostaje wielkością stałą.

6.

FALE W OŚRODKACH SPRĘZYSTYCH: RÓWNANIE FALI, MECHANIZM PROPAGACJI, WŁAŚCIWOŚCI RUCHU FALOWEGO, FALE AKUSTYCZNE I CECHY DŹWIĘKÓW.

Równanie fali:

y(x,t) = A⋅sin (ωt - kx) A - amplituda

Prędkość fali:

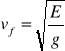
E - moduł Younga g - gęstość

Ruch falowy - Ruchem falowym nazywamy rozchodzenie się zaburzeń równowagi ośrodka sprężystego.

Impuls falowy - nazywamy rozchodzące się w ośrodku pojedyncze odkształcenie.

Właściwości fal:

- dyfrakcja - rozchodzenie poprzeczne, podłużne

- interferencja - załamanie

- odbicie - fale kuliste cząstkowe

Fala akustyczna (dźwiękowa):

Falą akustyczną nazywamy podłużną falę zagęszczeń i rozrzedzeń ośrodka, mogące rozchodzić się w ciałach stałych, ciekłych i gazach. Fale dźwiękowe obejmują pasmo częstotliwości od ok.16 do 20 000 Hz. Fale o częstotliwościach drgań niższych niż 16 Hz nazywane są infradźwiękami, wyższe niż 20 000 Hz nazywane są ultradźwiękami.

Cechy dźwięku:

-wysokość - zależy od częstotliwości drgań źródła

-barwa (brzmienie) - cecha charakterystyczna danego źródła dźwięku pozwalająca określić co wydaje dźwięk

-głośność (siła brzmienia) - wrażenie słuchowe uzależnione również od częstotliwości dźwięku

Mechanizm propagacji:

Niech źródło O tworzy falę poprzeczną. Punkt O znajduje się w ośrodku sprężystym i wykonuje drgania harmoniczne. W chwili t = 0 punkt O jest w położeniu równowagi, po 1/8 okresu T mija położenie A₁, po 2/8 T położenie A₂, po 3/8 T jest w A₃ (A₃=A₁), po 4/8 T punkt O przechodzi przez położenie równowagi A₄, po czym wychyla się w stronę przeciwną osiągając punkt A₅ po 5/8 T, punkt A₆ po 6/8 T, wraca do A₇ po 7/8 T, a po pełnym okresie znowu osiąga położenie równowagi. Dzięki siłom sprężystym drgania wykonywane przez punkt O udzielają się sąsiednim cząstkom ośrodka. Każda z tych cząstek zostaje wprawiona w analogiczne drgania jak punkt O, ale rozpoczyna swój ruch z pewnym opóźnieniem, zależnym od jej odległości od punktu O

7.

PRZEMIANY ENERGII W UKŁADACH ZAMKNIĘTYCH: 1-SZA I 2-GA ZASADA TERMODYNAMIKI, ENTROPIA I JEJ SENS FIZYCZNY.

I zasada termodynamiki:

Zmiana energii wewnętrznej ciała lub układu ciał jest równa sumie wykonanej pracy oraz ciepła wymienionego z otaczjącymi ciałami.

ΔU = Q + W

II zasada termodynamiki:

Niemożliwe jest zbudowanie silnika cieplnego, który pracowałby cyklicznie pobierając ciepło ze źródła bez możliwości przekazywania go do chłodnicy o niższej temp.

Entropia:

Entropia jest miarą nieuporządkowania. Stanom dużego nieuporządkowania odpowiada duża wartość entropii, natomiast stanom małego nieuporządkowania odpowiadają małe wartości entropii.

Jednostką entropii w układzie SI jest J/K

8.

ZAŁOŻENIE KINETYCZNO -MOLEKULARNEJ TEORII BUDOWY MATERII, RÓWNANIESTANU GAZU DOSKONAŁEGO I RZECZYWISTEGO , CIEPŁO MOLOWE GAZU , ROZKŁAD PRĘDKOŚCI DROBIN.

Założenia teorii kinetyczno -molekularnej budowy materii.

a)ciała mają budowę nieciągłą , składają się z drobnych elementów w postaci atomów lub cząstek(molekuł).

b)wymienione elementy budowy ciał są w ciągłym ruchu . Wartości liczbowe i kierunki prędkości poszczególnych elementów są różne .

c)pomiędzy poszczególnymi elementami budowy ciał występują siły wzajemnego oddziaływania .

Równanie stanu gazu doskonałego .

pv pv

------ = NK ----- = const.

T T

Równanie stanu gazu rzeczywistego .

a

( p + ---- ) (V - b ) = RT

V₂ Równanie Van Der Waalsa

Ciepło molowe gazu .

Molowym ciepłem właściwym gazu

nazywamy ilość ciepła jaką musi

wymienić z otoczeniem 1mol gazu ,

aby zmienić swą temperaturę o 1K

Q J

C_m = ------------ [ ------------- ]

mol ΔT mol K

8.

Rozkład prędkości drobin .

- niema wyróżnionego kierunku drobin

- wszystkie kierunki prędkości są prawdopodobne .

Prawo rozkładu prędkości Maxwella

1)zderzenia cząsteczek mają charakter doskonale sprężysty .

2)zgodnie z wymaganiami statystyki liczba cząsteczek dN , mających prędkości zawarte w dowolnie małym przedziale prędkości od V do V + dV, jest stała.

-V²

dN 4 V² ------

------ = ----- * ----- * e V²

N √π V³

N - ogólna liczba cząsteczek

dN - liczba cząstek odpowiadająca przedziałowi V i V + dV

V -prędkość najprawdopodobniejsza

9.

ŚREDNIA DROGA SWOBIDNA I LICZBA ZDERZEŃ DROBIN

ZJAWISKO PRZENOSZENIA W GAZACH , ZJAWISKO MOLEKULARNE W CIECZACH I CIAŁACH STAŁYCH . NAPIĘCIE POEIERZCHNIOWE I WŁOSKOWATOŚĆ .

Średnia droga swobodna cząsteczek.

V V 1

l = ------ = --------------- = --------------- υ 4√2 π r² n V 4√2 π r² n

V = 4√2 π r² n V - liczba zdarzeń

Zjawisko przenoszenia w gazach .

Przewodnictwo cieplne - zachodzi wtedy kiedy w gazie zachodzi różnica temperatur wywołana jakimiś przyczynami zewnętrznymi . Cząsteczki gazu w różnych miejscach objętości mają różne energie kinetyczne .

Zjawisko tarcia wewnętrznego (lepkość) - jest związana z powstaniem tarcia pomiędzy warstwami gazu albo cieczy przemieszczających się równolegle jedne względem drugich z prędkościami różnymi co do wielkości Warstwa poruszająca się szybciej daną siła przyspieszająca na warstwę , która porusza się wolniej i odwrotnie .

Siły tarcia , które przy tym powstają

Są skierowane stycznie do powierzchni przylegania warstw .

Dyfuzja - wzajemne przenikanie się gazów , cieczy oraz ciał stałych w wyniku przemieszczania się cząsteczek jednego pomiędzy cząsteczki drugiego

W przypadku mieszaniny gazów przyczyną dyfuzji jest różnica koncentracji poszczególnych gazów

W różnych częściach mieszaniny .

Teoria kinetyczna cieczy .

W cieczach istnieje bezładny ruch cząsteczek . Ruchy te nazywamy ruchami Browna . Ruchy te można traktować jako wynik zderzeń cząsteczek zawiesiny z cząstkami otaczającej cieczy .

Ciśnienie molekularne w cieczach .

Siła wypadkowa odniesiona do cząsteczek cieczy związanych z 1 m² jej powierzchni swobodnej wyraża liczbowo wartość ciśnienia molekularnego cieczy . Ciśnienie to jest skierowane w głąb cieczy , prostopadle do powierzchni swobodnej

Wartości ciśnienia molekularnego w cieczach są olbrzymie , rzędu tysięcy atmosfer .Tak wielkie ciśnienia tłumaczy mała ściśliwość cieczy .

Napięcie powierzchniowe .

Napięcie powierzchniowe sprawia , że ciecz ma zawsze najmniejszą powierzchnię możliwą w danych warunkach (np kulisty kształt kropli). Sprężyste fale poprzeczne mogą rozchodzić się po powierzchni cieczy również dzięki napięciu powierzchniowemu .

Współczynnik napięcia powierzchniowego - jest to współczynnik proporcjonalności , a zależy on od składu chemicznego i jej temperatury .Przy wzroście temperatury , ,,a” zmniejsza się osiągając wartość zero w temperaturze krytycznej .

Włoskowatość - ogół zjawisk wywołanych działaniem sił między cząsteczkowych jak np. tworzenie się menisków wklęsłych i wypukłych .

Menisk - zakrzywiona swobodna powierzchnia cieczy .

Menisk wypukły ciśnienie dopełniające

Δp > 0 .

Menisk wklęsły ciśnienie dopełniające

Δp < 0 .

10.

WRZENIE I PAROWANIE CIECZY .

ROZSZERZALNOŚĆ CIEPLNA CIAŁ STAŁYCH ,TOPNIENIE I KRZEPNIĘCIE .

Wrzeniem - nazywamy proces intensywnego parowania cieczy nie tylko z jej powierzchni swobodnej , ale również z całej objętości cieczy do wnętrza powstających wtedy pęcherzyków pary . Pęcherzyki pary we wrzącej cieczy szybko rosną i wypływają na powierzchnię .

Parowaniem - nazywamy proces zmiany cieczy w parę na powierzchni tej cieczy . Parowanie przebiega w każdej temperaturze . Ciecz paruje tym szybciej im ma większą temperaturę i większą powierzchnię swobodną . Szybkość parowania cieczy zależy ponadto od jej otoczenia .

Rozszerzalność cieplna .

t ₀ - temp . początkowa

l₀ - długość początkowa

t - temp . końcowa

l - długość końcowa (po rozszerzeniu)

Jeżeli Δt = t₀ jest nieduża , to przyrost długości Δl = l - l₀ jest proporcjonalny do przyrostu temperatury i do długości

początkowej .

l = l ₀ ( 1 + α Δt )

α - średni współczynnik rozszerzalności liniowej w granicach temperatur od t₀ do t .

l - l₀ 1

α = -------- [ ------- ]

l₀ Δt K

Niektóre ciała mają ujemny współczynnik rozszerzalności liniowej.

Ciepło molowe - nazywamy ilość ciepła potrzebną do ogrzania 1 mola tej substancji o temperaturze 1 K .

Q 1

C = ---------- [ ---------- ]

n ΔT mol K

Topnienie - jest to taki proces w którym substancja przechodzi z fazy stałej w fazę ciekłą .

Ciepłem topnienia - nazywamy ilość ciepła potrzebną na stopienie 1 kg ciała stałego ( bez zmiany temperatury ) .

Q J

q_t = ----- [ -------- ]

m kg

Krzepnięcie - nazywamy proces zmiany stanu skupienia z ciekłego w stały . Dla danej substancji ciepło topnienia i ciepło krzepnięcia ma tą samą wartość i oba procesy przebiegają

w tej samej temperaturze .

11.

OPTYKA GEOMETRYCZNA: KRZYWA WRAŻLIWOŚCI OKA, ODBICIE I ZAŁAMANIENA POWIERZCHNI GRANICZNEJ, WSPÓŁCZYNNIK ZAŁAMANIA ZWIERCIADŁA I SOCZEWKI; KONSTRUKCJA OBRAZÓW, RÓWNANIE ZWIERCIADŁA I SOCZEWKI, ZDOLNOŚĆ SKUPIAJĄCA

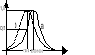
Krzywa wrażliwości oka

Oko ludzkie reaguje na długości fal w przedziale (4000-8000) czyli (4*10^-4÷8*10^-7)[m]

Oko reaguje na jasność - krzywa a

Oko reaguje na ciemność - krzywa b

Odbicie

Kąt odbicia βjest równy kątowi padania α. Promień padający, promień odbity i prostopadła padania leżą w jednej płaszczyźnie.

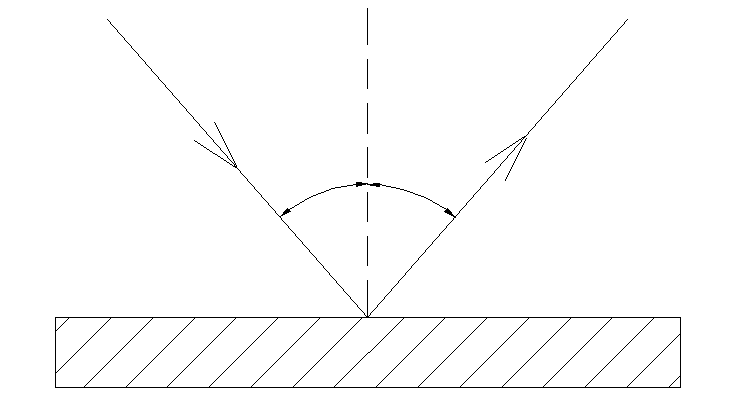
α=β

Równanie soczewki

f - ogniskowa soczewki

x - odległość przedmiotu od soczewki

y - odległość obrazu od soczewki

Prawo załamania światła

Dla danych dwóch ośrodków soczewek sinusa kąta padania do sinusa kąta załamania jest równy stosunkowi prędkości światła w ośrodku pierwszym do prędkości światła w ośrodku drugim i nosi nazwę współczynnika załamania światła ośrodka drugiego względem pierwszego. Promień padający, załamany i prosta prostopadła do płaszczyzny ograniczającej oba ośrodki leżą w jednej płaszczyźnie.

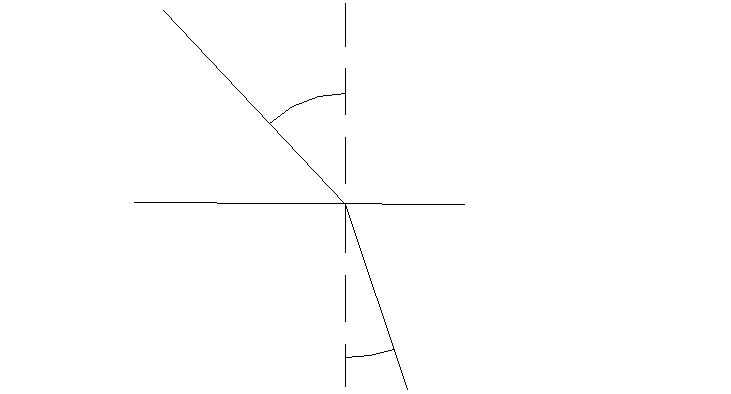
n₂₁ - współczynnik załamania światła ośrodka 1 wzgl. 2

α - kąt padania

β - kąt załamania

V₁ - prędkość światła w ośrodku 1

V₂ - prędkość światłą w ośrodku 2

Równanie zwierciadła kulistego

f - ogniskowa soczewki

x - odległość przedmiotu od soczewki

y - odległość obrazu od soczewki

Zdolność skupiająca soczewki

Zdolnością skupiającą soczewki nazywamy odwrotność jej ogniskowej („+” dla soczewek skupiających „-„ dla rozpraszających)

dioptria

Konstruowanie obrazów otrzymywanych za pomocą soczewek

W przypadku soczewek promienie charakterystyczne to:

a) promień biegnący do głównej osi optycznej soczewki, gdyż po załamaniu w soczewce przechodzi przez ognisko

b) promień przechodzący przez ognisko , gdyż po załamaniu w soczewce biegnie równolegle do głównej osi optycznej

c) promień przechodzący przez środek soczewki, gdyż nie ulega załamaniu

12.

OPTYKA FALOWA: INTERFERENCJA W CIENKICH WARSTWACH, PIERŚCIEŃ NEWTONA, DYFRAKCJAFRAUNHOFFERA NA SZCZELINIE, SIATKA DYFRAKCYJNA I JEJZASTOSOWANIE, POLARYZACJA ŚWIATŁA.

Interferencja światła w cienkich warstwach

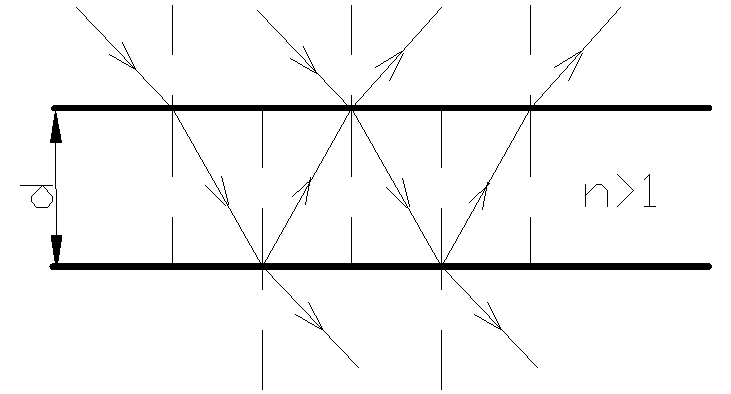
Uwzględniając zmianę fazy na przeciwną przy odbiciu od ośrodka optycznie gęstszego otrzymamy wyrażenie na różnicę dróg interferencyjnych promieni.

Różnica ta zależy od kąta padania α, od grubości płytki i jej współczynnika załamania. Jeżeli różnica równa się całkowitej wielokrotności λ padającego światła, to następuje interferencja wzmocnienia danej barwy. Jeżeli zaś różnica ta równa się nieparzystej wielokrotności λ/2 to następuje interferencyjne wygaszenie tej barwy. Warunki tworzenia się maximów i minimów interferencyjnych w świetle odbitym o cienkich warstw mają postać

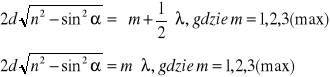
Siatka dyfrakcyjna

Najprostszą siatką dyfrakcyjną stanowi układ dużej liczby jednakowych co do szerokości szczelin leżących w jednej płaszczyźnie i rozdzielonych nieparzystymi odstępami o równej szerokości.

Siatki dyfrakcyjne wykorzystuje się w doświadczalnych metodach analizy widmowej światła

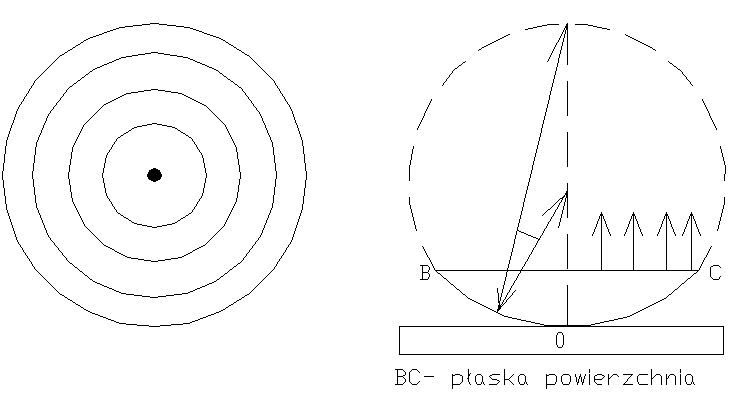
Pierścień Newtona

Płaskowypukła soczewka s o dużym promieniu krzywizny R powierzchni wypukłej położona jest na płaskiej płytce A, która styka się w punkcie 0. Równoległa wiązka światła pada prostopadle na płaską powierzchnię soczewki i ulega częściowemu odbiciu od jej sferycznej powierzchni oraz od górnej powierzchni płytki A. Przy nałożeniu się odbitych fal tworzą się ............. interferencyjne równej długości. W środku znajduje się ciemna plazma. Otoczona jest ona układem kolejnych jasnych i ciemnych pierścieni, których szerokość i intensywność stopniowo maleje w miarę zwiększania się odległości od plamy środkowej. W świetle przechodzącym obserwuje się zjawisko poboru, plama środkowa jest jasna, następny pierścień ciemny itd.

Polaryzacja światła

Dotyczy wyłącznie fal poprzecznych i polega na uporządkowaniu drgań ośrodka. Światło jest falą elektromagnetyczną, więc ma charakter fali poprzecznej. Kierunek polaryzacji fali elektromagnetycznej jest taki jak kierunek pola elektrycznego E. Światło w którym drgania pola elektrycznego odbywają się w różnych kierunkach nazywamy niespolaryzowanymi. Jego polaryzacja polega na uporządkowaniu drgań wektorów natężenia pola elektrycznego E .

Światło może być spolaryzowane:

- liniowo - drgania pola elektrycznego odbywają się tylko w jednym kierunku

- kołowo - kierunek drgań odbywa się ..........

Polaryzacja światła zachodzi podczas:

a)załamania; b)rozproszenia; c)odbicia

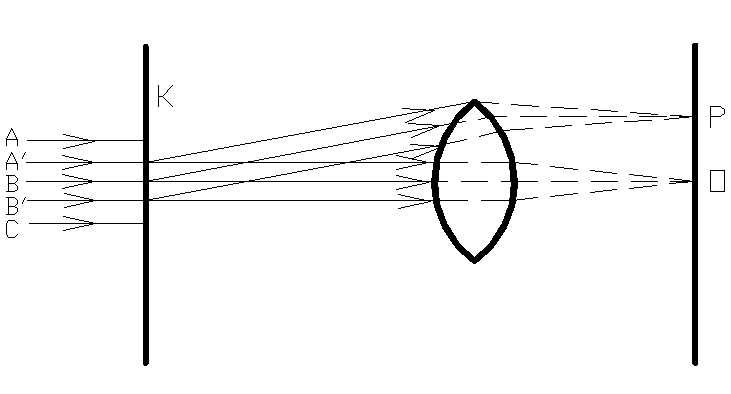
Dyfrakcja Fraunhoffera na szczelinie

Na szczelinę K pada fala płaska przedstawiona w postaci wiązki promieni równoległych. Poza szczeliną światło rozchodzi się nie tylko w kierunku przedłużenia promieni, lecz także dzięki ugięciu odchyla się od pierwotnego kierunku o kąty zawarte w granicach 0^o do 90^o. Każdy punkt szczeliny ugina światło.

13.

TEORIA KWANTÓW, PROMIENIOWANIE TERMICZNE CIAŁ, ZJAWISKO FOTOELEKTRYCZNE, PROMIENIOWANIE RENTG., ICH WYTWARZANIE I WŁAŚCIWOŚCI, EFEKT COMPTONA.

Promieniowanie termiczne ciał.

Jeżeli emisja fali elektromagnetycznej (świecenie) odbywa się kosztem np. energii chemicznej lub energii innego promieniowania pobudzającego do świecenia to mówimy o luminescencji.

W zależności od natury przejścia promienistego i stanu wzbudzonego układu świecącego rozróżniamy:

- fosforoscencja (stosunkowo długi czas zaniku)

- fluorescencja (fotoluminescencja o krótkim czasie zaniku)

- luminescencja rekombinacyjna

Jeżeli świecenie odbywa się kosztem energii cieplnej jaką posiada dana substancja to emitowane promieniowanie nazywamy termicznym.

Ciało doskonale czarne nazywamy ciało które całkowicie absorbuje padające na niego fale elektromagnetyczne.

Zdolnością absorbcyjną dowolnego ciała nazywamy stosunek absorbowanej energii do energii fali elektromagnetycznej padającej na dane ciało.

Zdolność absorbcyjna dla ciała doskonale czarnego

Zdolność emisyjna ciała nazywamy stosunek energii emitowanej w jednostce czasu przez jednostkę pola powierzchni do przedziału dγ częstotliwości emitowanych fal elektromagnetycznych.

Zdolność emisyjną ciała dostarczającego energię nazywamy gęstością widmową natężeń promieniowania emitowanego przez to ciało w danej temperaturze.

Energią dE_em=E(γ,T)dγ=hγdN_γ

Prawo przesunięć Wiena:

b=2,9*10^-3[K*m] stała Wiena

λ_maxT=b

T - temp. ciała dostarczanego dostarczającego energię

W miarę wzrostu temp. Ciała dost. energia ekstremalna wartość natężenia promieniowania jest emitowana dla fal o coraz krótszych długościach.

Całkowitą mocą emisyjną ciała o powierzchni ś określa wzór:

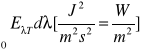
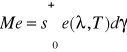
Prawo Stefana Boltzmana

M_f=δ_c*T⁴

δ=5,67*10^-8
] Stała Boltzmana

Całkowita moc promieniowania emitowanego przez ciało stosowane czarne rośnie do czwartej potęgi temp. tego ciała.

Zjawisko fotoelektryczne:

Zjawisko fotoelektryczne to wybijanie elektronów z metalu za pomocą promieniowania UV. Promieniowanie to jest wtedy gdy źródło światła ma temp. wyższą od 3000^oC.

Trzy prawa zjawiska fotoelektrycznego:

1. ilość wybitych elektronów jest wprost proporcjonalna do natężenia światła.

2. Prędkość wybitych z metalu elektronów jest wprost proporcjonalna do częstotliwości fali, a odwrotnie do długości fali.

3. dla każdego metalu istnieje długość graniczna począwszy od której zjawisko zachodzi w stronę fal krótszych:

Hipoteza Plancka o kwadratach energii stwierdziła, że energia promieniowania elektromagnetycznego jest emitowana ściśle określonymi porcjami

E = h*γ

Hipoteza Einsteina o fotonach, stwierdziła, iż energia promieniowania ściśle określonymi porcjami o energii określonej wzorem E = h*γ. Hipoteza ta pozwoliła wytłumaczyć zjawisko fotoelektryczne zewnętrzne i udowodniła niezależność energii wybijanych elektronów od natężenia światła padającego na dany materiał.

Zjawisko Comptona:

Zjawisko to polega na zmianie długości fali promieniowania elektromagnetycznego rozproszonego na elektronach można je wytłumaczyć korzystając z zasad zachowania energii i pędu, ale trzeba uwzględnić iż promieniowanie składa się z fotonów o energii posiadających pęd: p =

Promieniowanie Rentgenowskie (10^-8 + 10^-11) [m]:

Promieniowanie to powstaje podczas hamowania szybkich elektronów przez substancję. Otrzymywane jest ono za pomocą tzw. lampy rentgenowskiej.

Właściwości:

• zdolność jonizacji powietrza (bakterjobójcze)

• szkodliwe dla organizmów żywych

• powoduje świecenie minerałów i szkła (fluescencja)

• zdolność przenikania

• naświetlanie kliszy fotograficznej

• wszystkie cechy falowe

14.

TEORIA FAL MATERII DE BROGLIE'A I ZJAWISKO POTWIERDZAJĄCE TĘ TEORIĘ. BUDOWA ATOMU BOHRA, POSTULATY KWANTOWE

Postulaty Bohra i budowa atomu:

1.elektron w atomie wodoru może poruszać się po tzw. orbitach dozwolonych. Orbity dozwolone to takie, dla których jest spełniony następujący warunek:

2.Moment pędu elektronu poruszającego się po orbicie dozwolonej musi być równy całkowitej wielokrotności stałej Plancka podwojonej przez 2Π.

p = mVr

mVr = n_i *
i- wielokrotność

Elektron może krążyć w różnych odległościach od jądra, moment pędu będzie różny. Jeżeli elektron znajduje się na pierwszej orbicie to atom jest w stanie podstawowym. Jeżeli na innej orbicie to w stanie wzbudzonym.

Atom w stanie podstawowym:

r = 0,5*10^-8cm = 0,5 A

V*10

Elektron ma energię kinetyczną i potęcialną E =

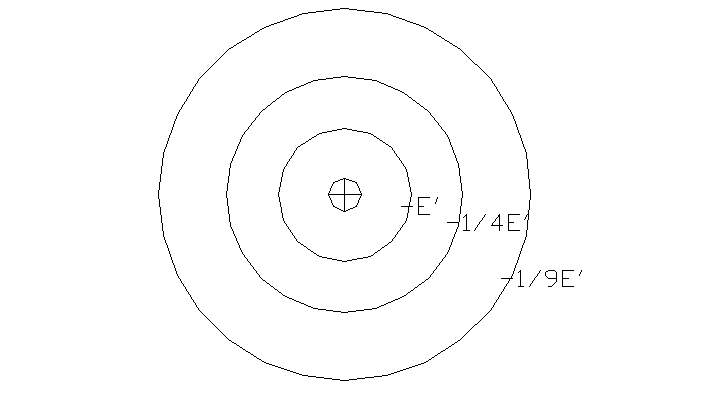
1.elektron krążąc po swojej orbicie nie zmienia swojej energii. Przy przeskoku z orbity bliższej na dalszą wypromieniowuje energię, a przy przeskoku z dalszej na bliższą wypromieniowuje energię w postaci kwantu.

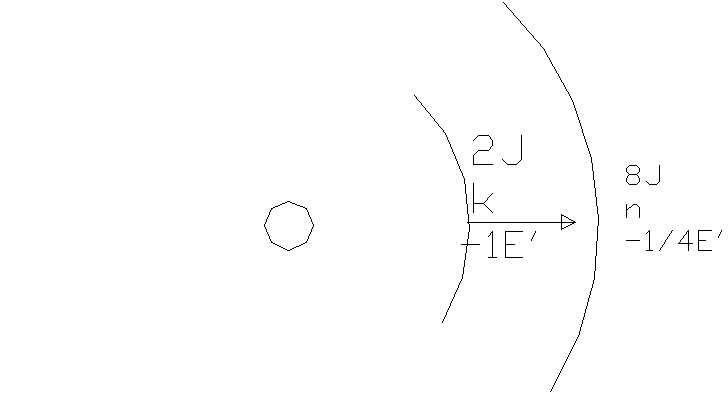
Dostarczanie energii powoduje przeskok.

Przejście ze stanu podstawowego do wzbogaconego może być spowodowane poprzez podwyższenie temp.

K < n E_n - K_k ..............

• c ...........

E_n - E_k =hγ

Elektron dąży do stanu podstawowego.

Elektron jest w stanie wzbudzonym≈10^-8 s.przy przeskoku z orbity nieskończenie dalekiejna drugą przyrost energii jest mniejszy niż z drugiej na pierwszą.

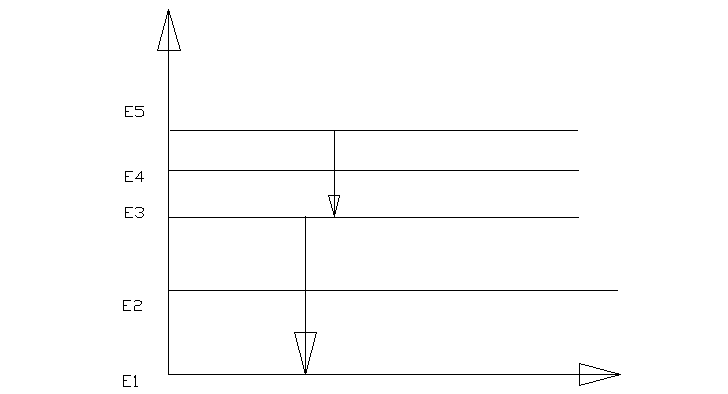
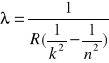
R - Stała Rydberga 1.09*10^..... [
]

λ - fala odpowiadająca przeskokowi elektronu z orbity dalszej na bliższą

Widmo:

Energia kwantu przy przeskoku na orbitę pierwszą jest tak duża, że nie widzimy tego i prążki widma leżące w świetle ultrafioletowym.

Zespół linii widmowych nazywamy serią widmową.

Seria Lymona - n = 1 -wszystkie linie widmowe leżą w ultrafiolecie (kanały duże)

Seria Balmena- n = 2 - leży w świetle fal widzialnych i powstaje przy wszystkich przeskokach na orbitę drugą

Seria Paschena- n = 3- leąy w świetle podczerwonym przy przeskoku z orbit dalszych na trzecią (małe kanały)

Seria Brockena n = 4

Seria Pfunda n = 5daleka podczerwień

Seria Humpresa n = 6

TEORIA FAL MATERII DE BROGKE'A

Światło ma dwie natury(dualizm korpuskularno- falowy )

- fala

- strumień cząstek, kwantów(natura korpuskularna )

Jeżeli światło pada na szczelinę to ujawnia się natura falowa. Jeżeli na metal to natura korpuskularna. Całe promieniowanie ma dwie natury. Masa kwantu to masa relatywistyczna .

Przemiana protonu w jądrze na neutron może się także dokonać przez wchłonięcie do jądra elektronu z jednej z powłok zewnętrznych najbliższych jądra np. z powłoki K lub L. Reakcja tego typu zwana jest przemiana K lub L.

4. Rozpad γ.

Rozpadowi jąder promieniotwórczych pierwiastków towarzyszy promieniowanie γ (elektromagnetyczne). Emitowane jest podczas przejścia jądra ze stanu wzbudzonego do stanu podstawowego albo do stanu o niższej energii, ........... pojawi się gdy jądro pochodne otrzymane w wyniku przemiany α lub β znajduje się w stanie wzbudzonym.

Detekcja promieniowania jądrowego - jest to wykrywanie promieniowania jądrowego.

a) detekcja jakościowa - komora Wilsona

klisze jądrowe

b) detekcja ilościowa - spintaryskop

licznik Geigera-Müllera

Jednostki

Aktywność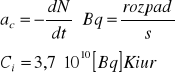

Dawka ekspozycyjna

Dawka pochłonięta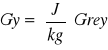

Biologiczny równoważnik dawki pochłoniętej

Hipoteza de Broojke'a stwierdza iż poruszającej się cząstce o pędzie p odpowiada tzw. Fala Broojke'a o długości

λ_B = h/p -stała Plancka.

Hipotezę zweryfikowali Dawisson i Germer. Charakterystyczne dla fal są zjawiska interferencji i dyfrakcji. Zjawiska te występują jedynie ,gdy fala napotyka na przeszkodę o wymiarach zbliżonych do jej długości. Dla cząstek zjawisko falowe zostanie zaobserwowane ,gdy elektrony natrafia na przeszkody o wymiarach rzedu 10^-10(m). Dawisson i Germer zauważyli to kierując wiązkę elektronów na kryształ w którym atomy są rozproszone od siebie w przestrzeni w odległościach ≅10^-10 (m)od siebie. Innym potwierdzeniem hipotezy Broojke'a jest obraz dyfrakcyjny elektronów przechodzących przez b. cienką polikrystaliczną fale ze złota. Obraz ten ma postać pierścieni Debyra-Scherera.

Promieniowanie stacjonarnych orbit atomu wodoru określa wzór :

Dozwolone wartości energii w atomie wodoru:

(poziomy energetyczne) określa wzór:

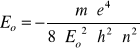
31

15. UOGOLNIENIA SOMMEFELDA : LICZBY KWADRATOWE OPISUJACE ZACHOWANIE SIĘ ELEKTRONU W ATOMIE I ICH SENS FIZYKALNY. KONFIGURACJA ELEKTRONOW W ATOMIE.

Sommerfeld wprowadził do modelu atomu orbity eliptyczne. Koło jest specjalnym przykładem elipsy gdyż oba ogniska zlały się w jednym punkcie.

4 liczby kwantowe opisuje zachowanie elektronów w atomie .

1). Liczba kwantowa główna n wiążąca się z energia elektronu na orbicie.

nr 1,2,3,4,5... (K,L,M,N,O,P,Q...)

2). Liczba kwantowo orbitalna l związana z momentem pędu na orbicie

l = 0,1,2,...,n-1 (s,p,d,f,g,h,)

gdy l = n-1 - elipsa przechodzi w koło.

* kształt orbity a/b = h/l+1

• orbitalny moment pędu

K-mvr =l h/2n

• orbitalny moment magnetyczny

p=l_μb

* energia E_n = me⁴ z /Bε h - 1/n

3). Liczba kwantowa magnetyczna m

Wektor l momentu pędu elektronu poruszającego się w atomie może przyjąć w przestrzeni tylko takie kierunki , dla których rzut l_z na wyróżniony kierunek, przyjmuje dyskretne wartości określone przez orbitalna magnetyczna liczbę kwantową.

l_z = k_m = m h/2π

m=-l; -l+1;-l+2;....;0;1;.....l-1;2

Liczba kwantowa spinowa s

Spin elektronu - nieorbitalny moment pędu związany z ruchem własnym elektronu dookoła własnej osi. Spin jest skwantowany i może przyjmować wartości.

Zasada Pauliego (zakaz)

Dwie jednakowe cząstki o spinie połówkowym nie mogą jednocześnie znajdować się samym stanie. Zakaz Pauliego dotyczy elektronów w atomie nie może być dwóch elektronów na tym stanie czyli o takich samych cienkich wartościachliczb kwantowych

Rozkład elektronów w atomach

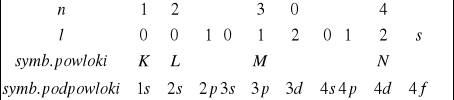
16.

WŁAŚCIWOŚCI SPRĘŻYSTOLEPKICH CIAŁ RZERCZYWISTYCH ODKSZTAŁCENIA SPRĘŻYSTE CIAŁ, PRAWO HOOK'A, MODUŁY SPRĘŻYSTOŚCI I LEPKOŚĆ PŁYNÓW, PRAWO HAGENA-MOMENTY OPORU RUCH CIAŁ W OŚRODKACH LEPKICH.

Prawo Hagena - Poissenla

liczba Reynoldsa

gdzie R_e<2300 - przepływ laminarny

R_e>3000 - przepływ burzliwy

Odkształcenia

Sprężyste

Prawo Hook'a-stosunek naprężenia do związanego z nim odkształcenia jest wielkością stałą dla danego materiału. Stosunek ten nazywamy modułem sprężystości.

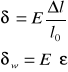
Moduły: W temp. 13^oC dla stali

- Younga E 2,19*10¹¹ N/m²

- sprężystości postaciowej G 0,83*10¹¹ N/m²

- sprężystości objętościowej K 1,7*10¹¹ N/m²

Lepkość -tarcie wewnętrzne

Przepływ nazywamy stacjonarnym gdy w określonym punkcie przestrzeni prędkość przepływu jest stała, niezależna od czasu.

Przepływ nazywamy stacjonarnym warstwowym lub laminarnym, gdy wszystkie cząstki płynu poruszają się po torach równoległych do siebie w tedy ruch płynu sprowadza się do przesuwania (poślizgu) warstw płynu względem siebie.

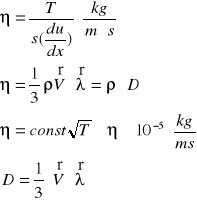
η - współczynnik lepkości

D - współczynnik dyfuzji

Prawo Bernoulliego

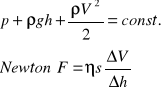
η - współczynnik lepkości charakterystyczny dla danego ośrodka

V_k - prędkość krytyczna przepływu płynu

Opory ruchu ciał:

Opływ laminarny F­­_op=6πη*V (wzór Stokes'a)

Opływ burzliwy

C_x - współczynnik oporów aerodynamicznych

17.

BUDOWA JĄDRA ATOMOWEGO, NUKLEONY I ICH CECHY, SIŁY JĄDROWE, ENERGIA WIĄZANIA, DETEKT MASY, PRZEMIANY JĄDER ATOMOWYCH I ZWIĄZANE Z TYM RODZAJE PROMIENIOWANIA JĄDROWEGO.

Proton + neutron =nukleon

_z^AX A-liczba masowa (nukleonu)

Z-liczba masowa (protony), decyduje o miejscu w układzie

Proton +e = 1,6021*10^-19 C

m_p=1,6725*10^-27 kg

m_p - jest 1836 razy większa m_c=9,109*10^-31kg

Izotopy-atomy danego pierwiastka mogą występować w różnych odmianach (liczba protonów nie zmienna, liczba neutronów zmienna)

Siły jądrowe - siły przyciągania małego zasięgu działające między nukleonami

Oddziaływanie silne

Oddziaływanie słabe

Energia wiązania - ilość energii jaką trzeba dostarczyć, aby jądro atomowe rozłożyć na poszczególne nukleony. Inaczej energia potrzebna do połączenia odpowiedniej ilości nukleonów w jądro atomowe.

Defekt masy - wynika z faktu że część masy zamieniane są na energię wiązania. Okazuje się jednak, że masa jądra nierówna się sumie mas składników i jest zwykle mniejsza od nich. Defekt masy Δm =(Σm_składników-m_jądra) może być łatwo przeliczony na energię ze wzoru:

E=Δmc²

Wynik uzyskany z takiego obliczenia przedstawia energię wiązania.

Przemiany jąder atomowych: rodzaje promieniowania

1.Rozpad α - polega na emisji z jądra cząstki α w wyniku tej przemiany liczba masowa jądra zmniejsza się o 4 a liczba atomowa o 2.

_z^AX→_z-2^A-4Y+₂⁴α

2.Przemiana β w czasie tej przemiany emitowane są z jądra elektrony pojawiające się w wyniku rozpadu neutronu na proton

₀¹n→₁¹p+_-1⁰e+₀⁰ν_e antyneutrino elektronowe

W wyniku tej przemiany liczba masowa jądra nie zmienia się, natomiast liczba atomowa rośnie o 1

3.Przemiana β⁺ - emitowane są pozytony (dodatnie elektrony) powstające w wyniku przemiany protonu w neutron.

18.

JEDNOSTKI PROMIENIOWANIA JĄDROWEGO, BUDOWA EAKTORA JĄDROWEGO ORAZ BOMBY ATOMOWEJ, REAKCJA TERMOJĄDROWA, ROZPAD JĄDER URANU.

Reakcja termojądrowa - polega na łączeniu się dwóch lekkich jąder w jądro cięższe. Reakcja ta zachodzi wówczas, gdy jądra w wyniku zderzenia zbliżają się do siebie na odległość mniejszą niż wynosi zasięg sił jądrowych. Jest to możliwe wtedy gdy reakcja zachodzi w bardzo wysokiej temperaturze.

Prawo rozpadu promieniotwórczego

Czas połowicznego zaniku

Średni czas życia jądra atomowego

Radioaktywność źródła

Jednostki promieniowania:

Radioaktywność - nazywamy liczbę rozpadów jąder atomowych danej substancji promieniotwórczej w jednostce czasu. Jednostką radioaktywności w układzie Si jest [Bq] bekerel. Jest to radioaktywność źródła w którym zachodzi 1 rozpad na 1 sekundę. Często spotykaną jednostką redioaktywności jest 1[Ci] kiur. Jest to radioaktywność źródła w którym zachodzi 3,7*10¹⁰ rozpadów na sekundę (1 gram radu).

Dawka ekspozycyjna - mierzymy w jednostkach [C/kg] lub [R] rentgen. Dawka ta wynosi 1[C/kg], gdy w jednym kilogramie napromieniowanego materiału zostanie wytworzony przez jonizację ładunek każdego znaku równy 1[C].

1[R]-jest dawką ekspozycyjną promieniowania, które w 0,001293[g] suchego powietrza wytwarza ładunek jonizujący równy jednostce elektrostatycznej ładunku

1[R]=2,58*10^-4 [C/kg]

Dawka pochłonięta - jest równa 1[Gy], gdy w 1 kg masy napromieniowanej substancji została pochłonięta energia promieniowania równa 1[J].

1[Gy]=1[J/kg]

Dawka 1 rada odpowiada pochłonięciu energii 100 ergów promieniowania w 1 gramie substancji

[1erg=10^-7J]; 1[rad]=10²[Gy*]

1[R]=8[erg/g]=8,8[mGy]

Jednostka biologicznego równoważnika dawki pochłoniętej

W układzie Si jest 1 [Si] Sivert

1[Si]=1[J/kg]

[rem]

1[rem]=100[erg/g]

1[rem]=10^-2[Si]

Rozpad jąder uranu

(uranowce)

(aktynowce)

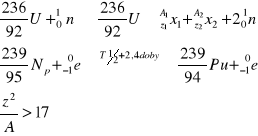
Dochodzi do rozpadu po bombardowaniu neutronami

termicznymi.

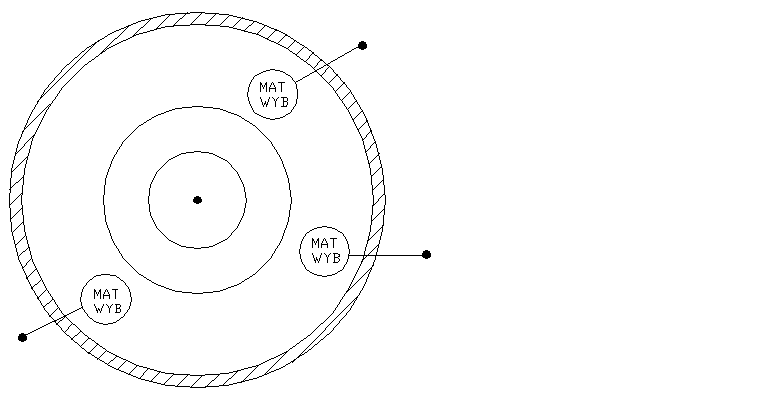
Bomba atomowa

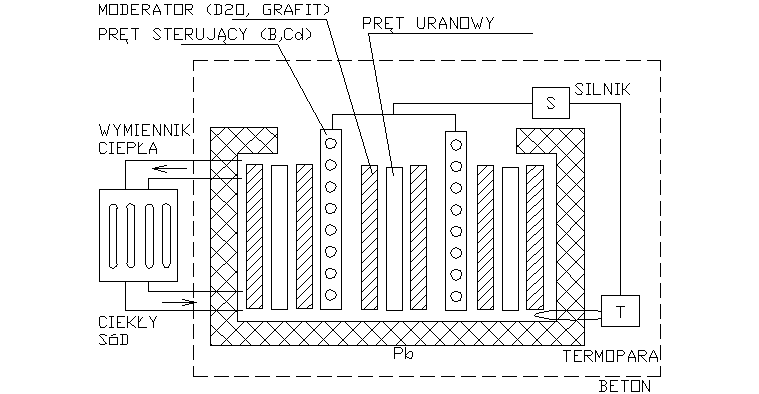
Budowa reaktora jądrowego

19.

CZĄSTKI ELEMENTERNE I ICH WŁAŚCIWOŚCI, KLASYFIKACJACZĄSTEK ELEMENTARNYCH. KWARKI JAKO PODSTAWOWE SKŁADNIKI MATERII.

Cząstkami elementarnymi nazywa się cząstki materii, które nie mają struktury wewnętrznej i nie można ich rozłożyć na mniejsze elementy.

Klasyfikacja

1) foton - cząstka elementarna(oddziaływanie elektrony)

2) lepton - nie bierze udziału w oddziaływaniach silnych

3) hadiony - wykazują strukturę wewnętrzną i są zbudowane z

kwarków

hadiony dzieli się na:

a) mezony

b) bationy: - hiperony

- nukleony

Mezon μ (mion) μ⁺, μ^-

Mezon π (pion) π^-, π⁰, π⁺

Neutrina mionowe νμ

Hiperony (Λ2182m_e, Σ2300m_e, Ξ2600m_e)

Pozyton, negaton (elektron)

Neutrino, antyneutrino (m_ν<5*10^-5m_e)

Kwarki - cząstki o ładunku uczestniczące w oddziaływaniach silnych. Mezony są zbudowane z dwóch a bationy z trzech kwarków powiązanych gmonami.

Praca pochodzi z serwisu www.e-sciagi.pl

β

α

n₁

I

II

n₂

β

α

Powstaje:

T~10⁷K

Fala uderzeniowa

Pr. Rentg. λ~10¹¹

Opad radioaktywny

Względne odkształcenie

Naprężenie normalne

---