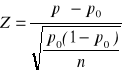TESTOWANIE HIPOTEZ STATYSTYCZNYCH dr Rumiana Górska

Hipotezą statystyczną nazywamy dowolne przypuszczenie (sąd), dotyczące parametrów lub postaci funkcyjnej rozkładu populacji generalnej.

Testem statystycznym nazywamy regułę postępowania, która każdej możliwej próbie losowej pobranej z populacji generalnej przyporządkowuje decyzję przyjęcia lub odrzucenia stawianej hipotezy.

Testy istotności to taki rodzaj testów, w których na podstawie wyników próby losowej podejmuje się decyzje o odrzuceniu H₀ z określonym małym ryzykiem popełnienia błędu I rodzaju, zwany poziomem istotności lub stwierdza się, że nie ma podstaw do jej odrzucenia.

Etapy przeprowadzenia testów istotności

1. Sformułowanie hipotezy zerowej H₀ oraz hipotezy alternatywnej H₁.

Stawiamy hipotezę zerową, że średnia m ma wartość m₀:

H₀:
,

wobec jednej z hipotez alternatywnych, w zależności od celów badania:

1⁰ H₁:
, 2⁰ H₁:
, 3⁰ H₁:
.

2. Wybór właściwego testu istotności. Obliczenie wartości statystyki testowej na podstawie próby.

Model	Test istotności dla średniej, gdy odchylenie standardowe σ jest znane, przy założeniu, że badana cecha ma rozkład normalny	Test istotności dla średniej, gdy odchylenie standardowe σ nie jest znane, a próba jest mała, przy założeniu, że badana cecha ma rozkład normalny	Test istotności dla średniej, gdy rozkład cechy i odchylenie standardowe σ nie są znane, a próba jest duża (n>30)	Test istotności dla wskaźnika struktury H0: , ( jest konkretną wartością hipotetyczną frakcji elementów wyróżnionych), wobec jednej z hipotez alternatywnych: 1^0H1: , 2^0H1: , 3^0 H1: .
Sprawdzian testu (statystyka testowa)

3. Konstrukcja obszaru krytycznego testu. Obszar krytyczny zależy od poziomu istotności, dlatego najpierw ustalamy odpowiedni poziom istotności α. W zależności od postaci hipotezy alternatywnej wyznaczamy dwustronny, prawostronny lub lewostronny obszar krytyczny.

1⁰H₁:
-dwustronny obszar krytyczny. K=
lub K=

2⁰ H₁:
- prawostronny obszar krytyczny, K=
lub K=
.

3⁰ H₁:
- lewostronny obszar krytyczny, K=
lub K=
.

4. Podjęcie decyzji weryfikacyjnej na poziomie istotności α:

Jeżeli obliczona na podstawie konkretnej próby wartość empiryczna Z_obl statystyki Z:

- przyjmie wartość z obszaru K (Z_obl
K), sprawdzaną hipotezę H₀ odrzucamy na korzyść hipotezy alternatywnej H₁,

- znajdzie się poza obszarem K (Z_obl
K), stwierdzamy jedynie, że nie ma podstaw do odrzucenia hipotezy H₀.

Zadania:

1. Producent czekolady z orzechami twierdzi, że zawartość orzechów w każdej 100-gramowej czekoladzie wynosi 30g. Chcąc upewnić się, że jest to prawda, decydujemy się zmierzyć zawartość orzechów przykładowo w 36 losowo wybranych czekoladach. Innymi słowy, zweryfikujemy hipotezę, że średnia zawartość orzechów w czekoladach wynosi 30g. Jest to hipoteza prosta, parametryczna, dotycząca wartości średniej m w populacji. Hipotezę tą zweryfikujemy na podstawie 36-elementowej próby losowej, zakładając, że zawartość orzechów w czekoladach, oznaczona jako X, ma rozkład normalny N(m,σ). Po przeprowadzeniu odpowiednich pomiarów stwierdzono, że średnia zawartość orzechów w próbie wynosi 31,5g z odchyleniem standardowym 3,06g, czyli
= 31,5g, s = 3,06g. Przeprowadzić odpowiedni test na poziomie istotności α=0,05 oraz α=0,01.

2. Maszyna pakietuje kawę w 100-gramowe opakowania. Wiadomo, że waga kawy, pakietowanej przez maszynę ma rozkład normalny. Na podstawie 20-elementowej próby losowej policzono, że średnia waga kawy wynosi 94g, a odchylenie standardowe wynosi 7g. Na poziomie istotności α=0,05 zweryfikować odpowiednią hipotezę, aby sprawdzić, czy maszyna pracuje prawidłowo.

3. W badaniu sprzed dwóch lat stwierdzono, że średni wiek bezrobotnych w województwie Śląskim wynosi 38 lat. Wysunięto hipotezę, że średni wiek bezrobotnych się zmniejsza. W związku z tym, wylosowano 60 bezrobotnych osób i stwierdzono, że ich średni wiek wynosi 35 lat z odchyleniem standardowym 8 lat. Czy można, zatem stwierdzić, że średni wiek bezrobotnych zmniejszył się przez ostatnie dwa lata? Badanie przeprowadzić na poziomie istotności α=0,01.

4. Wiadomo, że czas dojazdu studentów do szkoły ma rozkład N(m; 15). Stawia się hipotezę, iż przeciętny czas dojazdu nie przekracza 30 min. Aby sprawdzić tą hipotezę wylosowano 25 studentów i obliczono, że
=32 min. Przeprowadzić odpowiedni test na poziomie istotności α=0,04.

5. Menadżer zakładu obuwniczego otrzymał informację, że w sklepach pod koniec sezonu zostają męskie buty numer 40. Zlecił zatem, badanie czy odsetek produkowanych męskich butów numer 40, który wynosił do tej pory 20%, powinien się zmniejszyć. Zbadano 200 mężczyzn kupujących buty produkowane w zakładzie i stwierdzono, że 22 z nich nosi buty numer 40. Jaka powinna być odpowiedź dla menadżera, jeśli dopuszczalny jest błąd 1% (poziom istotności 0,01)?

6. Pewna nauczycielka języka polskiego wiedziała, że maturzyści popełniają średnio 2 błędy na stronę. Niezwykle zadowolona z postępów swoich uczniów, przypuszczała, że ich wyniki pod tym względem będą lepsze. Aby sprawdzić swoje przypuszczenia, postanowiła obliczyć błędy z 80 losowo wybranych kartek z prac pisemnych swoich uczniów i posłużyć się testem statystycznym. Policzyła, że średnia liczba błędów z próby wynosi
=1,8, a odchylenie standardowe s=0,8. Na poziomie istotności α=0,05 przeprowadzić test, aby sprawdzić czy przypuszczenia nauczycielki są słuszne.

7. Partia X zwyciężyła w ostatnich wyborach, otrzymując poparcie 70% wyborców. Przywódcy partii chcą sprawdzić, czy nadal mają takie same poparcie, czy być może odsetek ten się zmniejszył po ostatniej aferze korupcyjnej. Wylosowano próbę losową, składającą się z 1000 wyborców, i okazało się, że tylko 570 osób popiera partię.

a) Na poziomie istotności α = 0,10 przeprowadzić test istotności dla frakcji.

b) Na jakim najniższym poziomie istotności możemy utrzymać decyzje z a)?

1

---