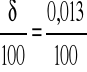MECHANIKA BUDOWLI
LABORATORIUM
ĆWICZENIE nr 14
TEMAT:
SKRĘCANIE SWOBODNE PRĘTA O PRZEKROJU PIERŚCIENIOWYM ZAMKNIĘTYM I OTWARTYM
WYKONALI:
Daniel Sulkowski
Marcin Sadowisk
Michał Łuczko
Sprawozdanie
Opis ćwiczenia
Celem ćwiczenia było porównanie pracy na skręcanie swobodne pręta o przekroju pierścieniowym zamkniętym i otwartym. Schemat statyczny obu prętów jest następujący:
Belka wykonana jest z mosiądzu: G=35000 Mpa
Doświadczenie 1
Skręcanie pręta o przekroju pierścieniowym zamkniętym
1. Opis doświadczenia:
Pręt został poddany działaniu momentu skręcającego. Stan przemieszczeń polega na sztywnym obrocie poszczególnych jego przekrojów (po skręceniu przekroje pręta są nadal płaskie).
-pręt obciążono momentem skręcającym M1 poprzez przyłożenie siły P=1 Kg na ramieniu r1=15 cm
-dokonano początkowych odczytów czujników zegarowych umieszczonych na końcu pręta (OPL) i w pobliżu jego utwierdzenia (OPP).
-ponownie obciążono pręt momentem M2 (siła P na ramieniu r2=65 cm)
-dokonano odczytów końcowych (OKL i OKP)
2. Tabela pomiarowa
Seria odczytów |
Nr punktu |
1 |
2 |
Odczyt I |
OP |
8,76 |
1,70 |
|
OK |
8,78 |
1,92 |
|
δ |
0,02 |
0,22 |
Odczyt II |
OP |
8,77 |
1,70 |
|
OK |
8,78 |
1,90 |
|
δ |
0,01 |
0,20 |
Odczyt III |
OP |
8,78 |
1,70 |
|
OK |
8,79 |
1,93 |
|
δ |
0,01 |
0,23 |
|
δ |
0,013 |
0,217 |
Kąty skręcenia pręta odpowiadające przyrostowi momentu skręcającego od M1 do M2
r1=0,15 m |
r2=0,65 m |
P=9,81 N |
P=9,81 N |
M1=P.r1=1,4715 Nm |
M2=P.r2=6,3765 Nm |
M=M2-M1=4,905 Nm |
|
a) L= |
b) p= |
Obliczenia teoretyczne kąta skręcania
G=35*10 9 Pa
R=0,019 cm
δ=0,001 cm
As= R2 =1,134115*10 -3 m2
![]()
a) dla l=0,5 m
L=13,62 10-3 rad
b) dla l=0,1 m
P=2,72.10-3 rad
Porównanie wyników doświadczalnych i teoretycznych
Kąt skręcenia w punkcie |
Wartość teoret. [10-3rad] |
Wartość doświad. [10-3rad] |
L |
13,62 |
13,0 |
P |
2,72 |
2,17 |
Doświadczenie 2
Skręcanie pręta o przekroju otwartym
Opis doświadczenia
Doświadczenie miało podobny przebieg jak dośw.1.
-pręt obciążono momentem skręcającym M1 poprzez przyłożenie siły P=0,1 kG na ramieniu r1=5 cm
-dokonano początkowych odczytów czujników zegarowych umieszczonych na końcu pręta (OPP) i w pobliżu jego utwierdzenia (OPL).
-ponownie obciążono pręt momentem M2 (siła P na ramieniu r2=20 cm)
-dokonano odczytów końcowych (OKL i OKP)
2. Tabela pomiarowa
Seria odczytów |
Nr punktu |
1 |
2 |
Odczyt I |
OP |
0,47 |
0,00 |
|
OK |
1,55 |
5,55 |
|
δ |
1,08 |
5,55 |
Odczyt II |
OP |
0,48 |
0,25 |
|
OK |
1,60 |
6,50 |
|
δ |
1,12 |
6,25 |
Odczyt III |
OP |
0,49 |
0,45 |
|
OK |
1,58 |
6,37 |
|
δ |
1,09 |
5,92 |
|
δśr |
1,1 |
5,91 |
Kąty skręcenia pręta odpowiadające przyrostowi momentu skręcającego od M1 do M2
r1=0,06 m |
r2=0,25 m |
P=0,981 N |
P=0,981 N |
M1=P.r1=0,05886Nm |
M2=P.r2=0,24525Nm |
M=M2-M1=0,18639 Nm |
|
a) L= |
b) p= |
Obliczenia teoretyczne kąta skręcania
G=35.109 Pa
R=0,019 m
δ=0,001 m
Is=![]()
(2R)δ3
=![]()
,![]()
a) dla l=0,1 m
L=0,01338 rad
b) dla l=0,5 m
P=0,06691 rad
Porównanie wyników doświadczalnych i teoretycznych
Kąt skręcania w punkcie |
Wartość teoret. [rad] |
Wartość doświad. [rad] |
L |
0,01338 |
0,011 |
P |
0,06691 |
0,0591 |
Uwagi własne
Wyniki doświadczeń oraz obliczeń teoretycznych nie pokrywają się w pełni, są jednak bardzo do siebie zbliżone. Doświadczenia przeprowadzone, więc zostały prawidłowo, a ewentualne różnice związane są z niedokładnością urządzeń pomiarowych jak i błędami odczytów.
Obliczenia (zarówno teoretyczne jak i doświadczalne) wyraźnie dowodzą, że kąt skręcania w przekroju otwartym jest dużo większy od kąta skręcania w przekroju zamkniętym, mimo że pręt o przekroju zamkniętym był obciążony większym momentem skręcającym (większa siła na większym ramieniu). Przekroje zamknięte są bardziej odporne na skręcanie niż przekroje otwarte.
400
Czujniki zegarowe
Wyszukiwarka
Podobne podstrony:
Mechaniki Budowli, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, mechanika budowli, MECHANIKA BUDOWL
Cw 10a, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, mechanika budowli, MECHANIKA BUDOWLI, Mechanik
mechana 13, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, mechanika budowli, MECHANIKA BUDOWLI, Mech
Mechaniki Budowli, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, mechanika budowli, MECHANIKA BUDOWL
Wydatki, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, złota, BUDOWN~1, Budownictwo przemysłowe
Kratownica płaska, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, złota, WYTRZY~1, Wytrzymałość mater
Linia ugięcia, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, złota, WYTRZY~1, Wytrzymałość materiałó
Teodolit, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, złota, GEODEZJA, Geodezja, Geodezja
Opis techniczny do projektu architektoniczno, NAUKA, budownictwo, BUDOWNICTWO sporo, Złota, złota, B
więcej podobnych podstron