PRACOWNIA ZAKŁADU FIZYKI PL
Radosław Michałek		Wydział Elektryczny Grupa EDi 2.1
Data wykonania ćwiczenia: 1999-03-03	Numer ćwiczenia: O 10.2	Temat ćwiczenia: Wyznaczanie skręcalności właściwej roztworów.
Zaliczenie:	Ocena:	Data:	Podpis:

1. Tabela pomiarów

L.p.	c	l	α1	α1	α2	α2	α	k	k
-	[kg/m^3]	[m]	[°]	[°]	[°]	[°]	[°]	[°m^2/k]	[rdm^2/k]
1	200	95*10^3	0,6	0,59	11,7	11,61	11,02	0,58	0,01
2										0,5		11,6
3										0,6		11,6
4										0,6		11,4
5										0,6		11,7
6										0,5		11,6
7										0,6		11,7
8										0,7		11,6
9										0,6		11,7
10										0,6		11,6
11										0,6		11,5
12										0,6		11,5

2. Obliczenia

3. Krótka teoria

Celem ćwiczenia jest wyznaczenie kąta skręcenia płaszczyzny polaryzacji.

Do badania skręcenia płaszczyzny polaryzacji używa polarymetrów. Polarymetr składa się z dwu nikoli polaryzującego i analizującego oraz lunetki. Światło po przejściu przez nikol P zostaje spolaryzowane liniowo. Nikol A możemy przez obrót ustawić w ten sposób, że kierunek drgań przepuszczanych przez niego będzie zgodny z kierunkiem drgań światła spolaryzowanego przez nikol P

Istotnym szczegółem w budowie polarymetru jest to, że kryształ jest wycięty i sklejony tak, że pole widzenia składa się z trzech części. Gdy wszystkie części są jednakowo oświetlone to jest to zero polarymetru

Dla roztworów wielkość kąta skręcenia płaszczyzny polarymetru wyraża się wzorem:

α=k*c*l

c=m/V

α- kąt skręcenia [°]

k - współczynnik charakteryzujący dany roztwór, zależny od rodzaju substancji rozpuszczonej i rozpuszczalnika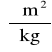

l - długość rurki polarymetrycznej w której znajduje się roztwór [m]

c- stężenie roztworu [kg/m³]

m- masa substancji rozpuszczonej [kg]

V- objętość rozpuszczalnika [m³]

4. Opis wykonania ćwiczenia

Pomiary rozpoczynamy od wyznaczenia zera polarymetru. Oświetlamy

polarymetr monochromatycznym sodowym źródłem światła i ustawiamy analizator w takie położenie, przy którym wszystkie części pola widzenia wydają nam się jednakowe. Za zero polarymetru przyjmujemy średnią z 12 pomiarów.

Następnie napełniamy rurkę polarymetru roztworem i wkładamy ją pomiędzy analizator i polaryzator. Przez obrót analizatora znajdujemy takie jego położenie, przy którym całe pole będzie jednakowo oświetlone. Ze skali odczytujemy kąt, jako wartość końcową przyjmujemy średnią arytmetyczną z 12 pomiarów.

5. Opracowanie wyników pomiarów

1. Błędy przypadkowe - metoda Gaussa

N=12

L.p.	c	l	α1	rα1=α1-α1	r^2α1	α2	rα2=α2-α2	r^2α1
-	[kg/m^3]	[m]	[°]	[°]	[°^2]	[°]	[°]	[°^2]
1	200	95*10^-3	0,6	0,01	10^-4	11,7	0,1	0,01
2			0,5	-0,09	8,1*10^-3	11,6	0	0
3			0,6	0,01	10^-4	11,6	0	0
4			0,6	0,01	10^-4	11,4	-0,2	0,04
5			0,6	0,01	10^-4	11,7	0,1	0,01
6			0,5	-0,09	8,1*10^-3	11,6	0	0
7			0,6	0,01	10^-4	11,7	0,1	0,01
8			0,7	0,11	0,0121	11,6	0	0
9			0,6	0,01	10^-4	11,7	0,1	0,01
10			0,6	0,01	10^-4	11,6	0	0
11			0,6	0,01	10^-4	11,5	-0,1	0,01
12			0,6	0,01	10^-4	11,5	-0,1	0,01
			Σα1=7,1 α1=0,59	Σrα1=0,02	Σr^2α1= 29,2*10^-3	Σα2=139,2 α2=11,6	Σrα1=0	Σr^2α2= 0,1

Średni błąd kwadratowy pojedynczego pomiaru (odchylenie standardowe)

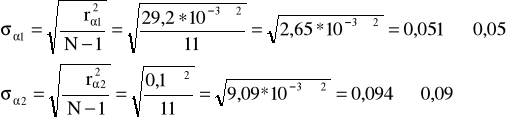
3σ_α1=3*0,05°=0,15° , więc wszystkie r_α1<3σ_α1

3σ_α2=3*0,09°=0,27° , więc wszystkie r_α2<3σ_α2

Wszystkie pomiary spełniają kryterium trzysigmowe dokładności

Błędy grube nie występują - pomiary wykonane prawidłowo

Średnie błędy kwadratowe średniej arytmetycznej

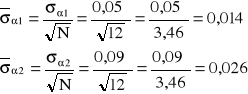
Średni błąd kwadratowy pomiaru pośredniego

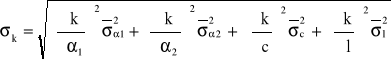
ponieważ c=const, σ_c=0 oraz l=const, to σ_l=0, a więc

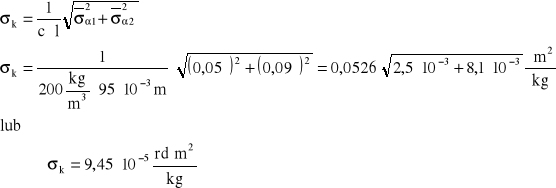
Obliczając współczynnik k

wynik pomiaru tej wielkości możemy zapisać następująco:

- przy kryterium jednosigmowym

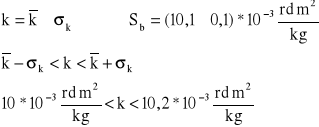
co oznacza, że w tym przedziale można z prawdopodobieństwem p=68,3% oczekiwać wartości rzeczywistej k

• Przy kryterium trzysigmowym (większa pewność wyniku)

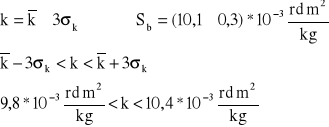
co oznacza, że w tym przedziale można z prawdopodobieństwem p=99,7% oczekiwać wartości rzeczywistej k

Określamy również:

- Błąd względny maksymalny

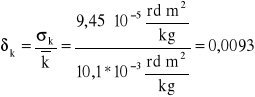
- Błąd przeciętny

- Błąd prawdopodobny

Błąd względny maksymalny - metoda różniczkowa

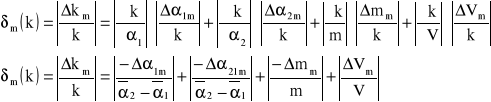
Δα_1m=Δα₁'+Δα₁''

Δα₁' - błąd bezwzględny pomiaru kąta wynikający z niedokładności skali polarymetru

Δα₁''=|α₁-α₁| , gdzie α₁- najbardziej różniący się od α₁

Δα₁'=0,1°

Δα₁''=|0,7°-0,59°|=0,11°

Δα_1m=0,1°+0,11°=0,12°

Δα_2m=Δα₂'+Δα₂''

Δα₂'=0,1°

Δα₂''=|11,4°-11,61°|=0,21°

Δα_2m=0,1°+0,21°=0,22°

ΔV=0,5 cm³ - błąd pomiaru roztworu

Δm=10mg - błąd pomiaru masy (wartość najmniejszego odważnika)

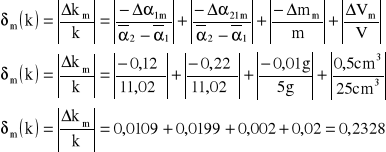
δ_m(k)=0,2328 ≈ 0,23

δ_m[%](k)=23%

1

6

---