Data wykonania ćwiczenia: 13.03.2007 r.

Politechnika Szczecinska

Katedra Budownictwa wodnego

Sprawozdanie z ćwiczen laboratoryjnych z hydrauliki

Ćwiczenie nr 2

Temat: „Wyznaczanie rzednych linii cisnien i linii energii w przewodach kołowych pod cisnieniem”

Rok I

Grupa III

Skład zespołu:

- Straczko Wojciech

- Szlingiert Paweł

• Pozyczka Piotr

1. Wstęp teoretyczny:

Do wyznaczenia linii ciśnień i linii energii w rurociągu hydraulicznym korzystamy z równań Bernulliego.

• linia ciśnień - wykres piezometryczny nadciśnień statycznych wzdłuż rozpatrywanego rurociągu,

• linia energii - wykres energii mechanicznej cieczy wzdłuż rozpatrywanego rurociągu,

• równanie Bernulliego:

• dla cieczy doskonałej:

gdzie:

z - wysokość położenia, tj. rzędne osi rurociągu dla przekroju,

- wysokość ciśnienia w przekroju,

- wysokość prędkości, tj. wielkość średniej prędkości przepływu w przekroju.

Rys.1 Linia ciśnień i energii w cieczy doskonałej.

Linia energii jest linią poziomą ponieważ straty energii nie występują. W życiu jest to niemożliwe.

• dla cieczy rzeczywistej

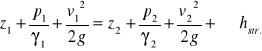
gdzie:

- rzędne osi rurociągów dla przekrojów,

,
- wysokości ciśnienia w przekrojach,

,
- wielkość średnich prędkości przepływu w przekrojach

- suma wielkości strat na pokonanie oporów ruchu między przekrojami.

Rys.2 Linia ciśnień i energii w cieczy rzeczywistej.

Dla cieczy rzeczywistej cześć energii, jaką struga przepływająca między dowolnie wybranymi przekrojami jest zużywana na pokonanie oporów ruchu wywołanych głównie lepkością cieczy i chropowatością ścian przewodu. Energia kinetyczna zmienia się w energię cieplną i występują straty energii mechanicznej.

Na sumę strat energii składają się:

• Straty lokalne: wynikajace z napotkanych przeszkód przez płynąca ciecz

gdzie:

v - prędkośc przeplywu za przeszkodą

ζ - współczynnik strat lokalnych zależny od rodzaju napotkanej przeszkody,:

g - przyśpieszenie ziemskie (
)

Rodzaje strat lokalnych:

1. na wlocie:

wlot pod kątem

wlot prosty ζ = 0,5

wlot profilowany ζ = 0,25

wlot krzywoliniowy ζ = 0,005 - 0,1

2. na krzywaku (kolanku):

3. przy poszerzeniu:

4. przy przewężeniu:

5. na zaworze:

straty zależne są od typu zaworu i średnicy na jakiej jest zamontowany

6. przy załamaniu przewodu:

g) na wylocie

• Straty na długości: wynikające z tarcia cieczy o ściany przewodu, ich wielkość jest proporcjonalna do długości przewodu (wzór Darcy Weisbacha):

gdzie:

d - średnica przewodu

L - długość przewodu

λ - współczynnik tarcia wg Colebrooka - White'a, przedstawiony jako funkcja = ( Є , Re),

i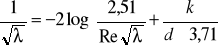

gdzie:

Re - liczba Reynoldsa,

- rzędna funkcji , Є = k/d, gdzie:

k - chropowatość powierzchni rury przez która przepływa ciecz,

d - średnica przewodu

Chropowatość - cecha powierzchni ciała stałego, oznacza rozpoznawalne optyczne lub wyczuwalne mechanicznie nierówności powierzchni, nie wynikające z jej kształtu, lecz przynajmniej o jeden rząd wielkości drobniejsze.

Liczba Reynoldsa - jedna z liczb podobieństwa stosowanych w reologii. Przy jej pomocy można oszacować stosunek sił bezwładności do sił lepkości. Liczba Reynoldsa jest kryterium do wyznaczania charakterystyki przepływu wszelkich płynów nieściśliwych.

Wydatek - ilość cieczy przepływającej przez przekrój w czasie

,

2. Zastosowanie w praktyce:

Obliczanie strat lokalnych, na długości oraz wysokości linii ciśnień ma zastosowanie w planowaniu magistral oraz sieci wodociągowych. Jest niezbędne również podczas projektowania instalacji i sieci sanitarnych oraz dobieranie urządzeń sanitarnych tak aby powodowały one minimalne straty hydrauliczne. Przykładem mogą być straty na rozdzielaczach CO oraz różnego rodzaju pompach stosowanych w budownictwie (np. pompy rotacyjne). Ważnym elementem jest również obliczanie strat hydraulicznych w kanałach przepływowych, wodnych, a tym samym dobieranie odpowiedniego przepływu oraz na odwrót - dobieranie przepływu do strat. Liczenie strat hydraulicznych jest uniwersalne zarówno do układów wodociągowych otwartych jak i zamkniętych oraz układów pod hydrotransport (gdzie bardzo ważna jest jak najmniejsza ilość strat ze względu na opłacalność transportowania). Umiejętność liczenia strat może też nam posłużyć do znajdowania nieszczelności w układach uprzednio przez nas zbudowanych.

Czasem potrzebne jest również obliczanie straty hydraulicznych w obliczeniach hydrogeologicznych.

3. Kolejność czynności:

1. Otworzyć dopływ do stanowiska i pomierzyć wzniesie zwierciadła wody w zbiorniku.

2. Otworzyć odpływ z przewodu maksymalnie i jednocześnie kontrolować stały poziom wody w zbiorniku zasilającym.

3. Pomierzyć wydatek dwukrotnie.

4. Odczytać wysokości linii ciśnień w rurkach piezometrycznych.

5. Zmierzyć temperaturę wody w zbiorniku zasilającym.

4. Cel doświadczenia:

Zbadanie strat na poszczególnych przeszkodach oraz na długości podczas przepływu cieczy przez układ rur.

5. Rysunek stanowiska (inwentaryzacja):

6. Wyniki pomiarów i obliczenia:

Lp.	Przyczyna strat	h [cm]
1	Poziom wody w zbiorniku	106,8
2	Na wlocie i na długości	105,6
3	Na dwóch kolankach i na długości	105,2
4	Na długości	104,9
5	Na poszerzeniu	104,3
6	Na długości	104,3
7	Na przewężeniu	101,4
8	Na długości i na łuku	98
9	Na zwężce	94
10	Na zwężce	97
11	Na długości	95
12	Na zaworze	79,2
13	Na długości	78,3
14	Na załamaniu	75,5
15	Na długości	74,2
16	Na przewężeniu	66,4
17	Na długości	40,5

Chropowatość k = 0,15 [mm]

Lepkość dynamiczna υ = 0,01057

Średnica d = 39 [mm]

Natężenie przepływu Q

««« Przykładowe obliczanie strat na długości:

1)

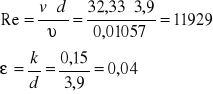
Współczynnik tarcia λ=0,042

««« Przykładowe obliczanie strat lokalnych:

2)

Współczynnik strat lokalnych dla zaworu ζ=10,8

7. Wnioski:

-Największe straty lokalne występują na zaworze.

-Wraz ze zwiększaniem się długości rury straty na długości rosną.

-Im mniejsza średnica rury tym większa prędkość cieczy znajdującej się w niej, a tym samym większa wysokość linii energii.

-Błędy pomiarowe mogą występować podczas pomiaru wysokości ciśnienia w rurkach piezometrycznych, pomiaru czasu podczas mierzenia natężenia przepływu, pomiaru wysokości wody w zbiorniku wylewowym, niedokładności stopera oraz suwmiarki.

8. Literatura:

• Książyński K.: Hydraulika, Kraków, PK 2000

• Walden H.: Mechanika płynów, Warszawa, WPW 1988

• Szuster A., Utrysko B.: Hydraulika i podstawy hydromechaniki, PW 1992

9. Załączniki:

• Wykres nr 1 „linia ciśnień i energii w rurkach piezometrycznych 1-17”

• Wykres nr 2 „linia ciśnień i energii w rurkach piezometrycznych 10-17”

---