Egzamin z matematyki dyskretnej 29 czerwiec 2005
Imię: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Nazwisko: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Grupa: |
|
Numer Indeksu: |
|
|
|
|
|
|
|||||||||||||||||
Uwagi:
Czas rozwiązywania 100 minut.
Ewentualne wątpliwości związane z niejednoznacznością sformułowań w zadaniach należy umieścić obok udzielonych odpowiedzi.
Dozwolone jest korzystanie z pomocy w formie własnoręcznych notatek i wydruków slajdów z wykładu. Nie wolno korzystać z książek i urządzeń elektronicznych.
Zbiór liczb naturalnych nie zawiera zera: 0 ∉ N.
Zapis "a | b" oznacza "a jest dzielnikiem b" czyli "b jest podzielne przez a".
W trakcie egzaminu nie wolno opuszczać sali przed oddaniem pracy.
Skala ocen jest opisana notacją (a/b/c) gdzie a - liczba pkt. za poprawną odp., b - liczba pkt. za brak odp., c - liczba pkt. za błędną odp.
Za żadne z siedmiu zadań nie można uzyskać mniej niż 0 pkt.
Rozwiązania zadań 6, 7 należy umieścić na osobnej kartce.
Zad. 1. (10 pkt. 2/0/0) Na ile sposobów można utworzyć słowo 10 literowe:
z liter a, b, c tak, aby każda z nich wystąpiła co najmniej raz.......... 310 - 3⋅210 + 3
z 3 liter a i 7 liter b..............10! / (3!⋅7!)
z 3 liter a i 7 liter b tak, aby żadne dwie litery a nie sąsiadowały ze sobą......................... .....8! / (3!⋅5!)
z liter a, b, c tak aby po żadnym c nie występowało a ani b oraz aby po żadnym b nie występowało a (litery muszą być ułożone alfabetycznie) .... 12! / (2!⋅10!)
z liter a, b, c, d, e tak, aby każda z nich wystąpiła dokładnie 2 razy... 10! / 25
Zad. 2. (9pkt. 1/0/0) Niech A = {1, 2, ..., 10}. Dana jest relacja S ⊆ A2, gdzie xSy ⇔ 3 | x + y ∧ x < y. Relacja R stanowi przechodnie domknięcie zwrotnego domknięcia relacji S (R = p(z(S))).
Czy relacja R jest porządkiem częściowym? .............Tak...................
Jeżeli tak, to wyznacz:
{x ∈ A : xR5}................................1, 2, 4, 5
{x ∈ A : 5Rx}................................5, 7, 8, 10
wysokość R ................................ 7
szerokość R................................2
wszystkie elementy maksymalne w A względem R.....9, 10
wszystkie elementy minimalne w A względem R......1, 3
najdłuższy łańcuch w A względem R...1, 2, 4, 5, 7, 8, 10
najdłuższy antyłańcuch w A względem R....np. 1, 3
Zad. 3. (8 pkt. 1/0/-0.5) Dla grafu G na rysunku poniżej wyznacz
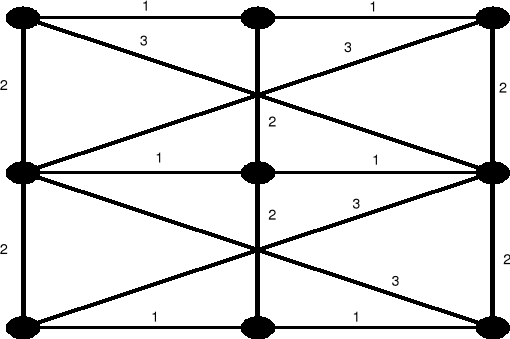
Długość optymalnej trasy chińskiego listonosza...............36
Wagę minimalnego drzewa spinającego................................10
Spójność wierzchołkową................................3
Długość najdłuższego cyklu................................8
Promień................................2
Średnicę................................3
Liczbę chromatyczną G................................2
Indeks chromatyczny G................................5
Uwaga:wagi przypisane krawędziom mają znaczenie wyłącznie dla pierwszych dwóch problemów. Dla pozostałych sześciu należy je zignorować.
Zad. 4 (7 pkt. 2/0/0) Uporządkuj według niemalejącego tępa wzrostu następujące funkcje (tak, że jeśli f występuje przed g, to zachodzi f = O(g)):
f1(n) = log2n + n1/2 + 3n / n2
f2(n) = log3n3 + n1/3 + 2n / n
f3(n) = n1/2logn + 2n / 3n
f4(n) = (1+1/n)n + n1/2
f5(n) = (4/3)n + n1/2
f6(n) = 2005! ⋅ n2005
4
|
3 |
6 |
5 |
2 |
1 |
Zad. 5 (8 pkt. 2/0/0) Przedstaw przykłady relacji równoważności R ⊆ N2 takiej, która:
Ma nieskończenie wiele klas abstrakcji, z których każda jest nieskończona
xSy ⇔ y = 2x
R = p(s(z(S)))
Ma nieskończenie wiele skończonych i nieskończenie wiele nieskończonych klas abstrakcji
xSy ⇔ y = 2x ∧ 2 | y
R = p(s(z(S)))
Ma 2005 klas abstrakcji, z których każda jest nieskończona
xRy ⇔ 2005 | (x - y)
Ma 2005 skończonych klas abstrakcji i jedną nieskończoną klasę abstrakcji
xRy ⇔ (x = y ∧ x < 2006) ∨ (x ≥ 2006 ∧ y ≥ 2006)
Każdą z odpowiedzi uzasadnij.
Zad. 6 (9 pkt. 9/0/0) Wyznacz zwarty wzór na n-ty wyraz sumy:
![]()
Uzasadnij poprawność uzyskanego wzoru.
![]()
Zad. 7 (9 pkt. 9/0/0) Niech Bn oznacza liczbę wszystkich podziałów zbioru n elementowego. Udowodnij, że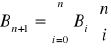
. (łatwo zauważyć, że początkowe wyrazy wynoszą odpowiednio B0 = 1, B1 = 1, B2 = 2, B3 = 5, ...)
Niech X będzie dowolnym zbiorem n + 1 elementowym. Wybierzmy pewien element x ∈ X. Sposób generowania podziału X przebiega w dwóch fazach. Najpierw wybieramy n - i elementów, które trafią do tego samego podzbioru co element x a następnie dokonujemy dowolnego podziału na podzbiory pozostałych i elementów. Mamy pewność, że każdy możliwy podział może być w ten sposób wygenerowany oraz, że dwa różne wybory w pierwszym kroku nigdy nie doprowadzą do uzyskania takiego samego podziału zbioru X.
Dla ustalonego i pierwszy krok można wykonać na ![]()
sposobów a drugi na ![]()
sposobów. Stąd ostatecznie dla ustalonego i liczba wszystkich sposobów wynosi ![]()
.
Należy rozważyć wszystkie przypadki 0 ≤ n - i ≤ n czyli 0 ≤ i ≤ n. Stąd otrzymujemy końcową formułę 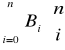
.
Wyszukiwarka
Podobne podstrony:
DEgz2-2007-rozw, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2010 rozw, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2009 rozw, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2007-rozw, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2005, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2006, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2007, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2005, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2008 zakres 2007-2008, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2009, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2010, AA informatyka - studia, cwiczenia i egzaminy
Zad02 relacje binarne, AA informatyka - studia, cwiczenia i egzaminy
Zad03 relacje binarne-domkniecia, AA informatyka - studia, cwiczenia i egzaminy
Zad04 zliczanie, AA informatyka - studia, cwiczenia i egzaminy
więcej podobnych podstron