Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej

Ćwiczenie to polega w pierwszej części na wyliczeniu stałej siatki na podstawie pomierzonego rzędu widma. W drugiej części ćwiczenia zajmiemy się wyznaczeniem długości fali świetlnej : niebieskiej, zielonej i żółtej, na podstawie pomierzonych rząd widm na prawo i na lewo.

Wprowadzenie

Światło widzialne jest to promieniowanie slektromagnetyczne, na które reaguje oko ludzkie. Zakres długości fal tego promieniowania wynosi od 3,8 *10^-7 m do 7,7 *10^-7 m. Do światła zalicza się również promieniowanie podczerwone i nadfioletowe. Długość faliλ równa jest odległości pomiędzy punktami przestrzeni, w których fala jest w tej samej fazie. Czas jaki fala potrzebuje na przebycie drogi równej długości fali, nazywamy okresem fali T.

Światło ma naturę dualną, falowo-korpuskularną; przyjmuje się, że światło to swego rodzaju strumienie osobliwych cząstek ( korpuskuł ), zwanych fotonami, które wykazują własności falowe. Na falową naturę światła wskazują takie fakty doświadczalne jak dyfrakcja i interferencja promieni świetlnych. Zjawisko dyfrakcji i interferencji światła możemy zaobserwować wykorzystując siatkę dyfrakcyjną. Najprostszą siatkę dyfrakcyjną stanowi przezroczysta płytka z gęsto ponacinanymi , równoległymi rysami. Rysy odgrywają rolę przesłon, a przestrzenie między rysami to szczeliny. Odległość między rysami nazywana jest stałą siatki dyfrakcyjnej d. Siatka dyfrakcyjna jest używana do analizy widmowej i pomiarów długości fali światła.

Światło przechodzące przez siatkę dyfrakcyjną ugina się na szczelinach, bowiem zgodnie z zasadą Huygensa każda szczelina staje się źródłem nowej fali wysyła promienie we wszystkich kierunkach. Zjawisko uginania się fali na otworach bądź krawędziach przesłon nazywamy dyfrakcją , czyli uginaniem prostoliniowego biegu promieni. Ugięte wiązki padające w to samo miejsce ekranu ulegają interferencji. Interferencją fal nazywamy nakładanie się fal o tej samej częstotliwości, powodujące wzmocnienie lub osłabienie natężenia fali wypadkowej. W tych miejscach ekranu, w których ugięte promienie spotykają się w zgodnych fazach, następuje ich wzmocnienie i powstają jasne prążki inetrferencyjne.

Promienie spotykające się w tym samym miejscu ekranu w fazach przeciwnych ulegną wzajemnemu wygaszeniu i na ekranie otrzymamy ciemny prążek. Warunkiem uzyskania minimum dyfrakcyjnego jest, aby różnica dróg dwóch sąsiednich promieni była równa nieparzystej wielokrotności długości fali :

dsinλ_n=( 2n+1)λ / 2

Wyraźny obraz dyfrakcyjny ( ostre prążki jasne i ciemne ) otrzymuje się wówczas, gdy stała siatki jest porównywalna z długością fali uginanego światła. W typowych siatkach dyfrakcyjnych liczba rys na 1mm wynosi od ok. 1200 dla nadfioletu do 300 dla podczerwieni.

Wyznaczenie stałej siatki d

Po włączeniu źródła światła monochromatycznego o znanej długości fali λ_s odczytujemy położenia linii widmowych dla kilku rzędów po lewej i po prawej stronie szczeliny. Obliczamy dla każdego rzędu średnie odległości prążków od szczeliny :

X_n=( x₁+x₂) / 2

Następnie obliczamy sinus kąta ugięcia

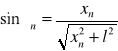
i odczytujemy kąt ugięcia α_n.

Dla każdego rzędu obliczamy stałą siatki d ze wzoru

Następnie obliczamy jej średnią wartość ze wzoru d = ( d₁+ d₂+d₃ ) / 3

Wyznaczanie długości fali świetlnej

Za szczeliną ekranu ustawiamy lampę rtęciową i notujemy położenia linii widmowych na lewo i na prawo od szczeliny. Odczytu dokonujemy dla trzech rzędów , intensywnie świecących prążków barwy niebieskiej, zielonej i żółtej. Na podstawie tych odczytów obliczamy dla każdego rzędu średnią odległość prążka od szczeliny na podstawie wzoru

a_n=( a₁+a₂ ) / 2 . Znajdujemy kąt ugięcia i długość fali

Dla każdej barwy obliczamy wartość średnią długości fali : λ = ( λ₁ + λ₂+ λ₃ ) / 3

Poniższe tabele przedstawiają wyniki obserwacji doświadczenia.

Długość fali światła sodowego λs [ nm ]	632,8
Odległość siatki od ekranu l [ m ]	1

Wyznaczanie stałej siatki d

Rząd widma	Odl. od szczeliny [ m ]			Kąt ugięcia λn	Stała siatki dn	Śr.stała siatki d
		na prawo	na lewo				Średnie
n	xp	xl	xn	[stopnie]	[nm]	[nm]
1	0,128	0,127	0,127	7,26	5022,22	5020,04
2	0,126	0,126	0,126	14,63	5002,37
3	0,407	0,409	0,408	22,19	5035,54

Wyznaczanie długości fali świetlnej λ

Barwa linii widmowych		Niebieska λtab=435,1 nm			Zielona λtab=546,1 nm			Żółta λtab=578,0 nm
Rząd widma n		1	2	3	1	2	3	1	2	3
Odl.od szczel. [m]	Na pr.	0,064	0,125	0,190	0,079	0,159	0,247	0,084	0,168	0,263
		Na lew	0,061	0,127	0,192	0,075	0,161	0,246	0,083	0,170	0,265
		Śr.	0,625	0,126	0,191	0,077	0,160	0,2465	0,835	0,169	0,264
Kąt ugięcia [°]		3,61	7,18	10,81	4,40	9,90	13,83	4,77	9,59	14,79
Dł. Fali λn [nm]		316,08	313,72	313,84	385,13	396,54	399,99	417,44	418,16	427,16
Śr.dł. fali [nm]		λI=314,54			λII=393,88			λIII=420,92
Δλtab=λ-λtab		120,56			152,22			157,08
(Δλtab / λtab)*100%		27,70%			27,87%			27,17%

Rachunek błędu dla widma niebieskiego

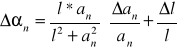
Δα₁=0,0043

Δλ₁=4,57

Δα₂=0,0034

Δλ₂=21,78

Δα₃=0,0036

Δλ₃=14,19

---