CECHY KSZTAŁTU PODŁUŻNEGO STRZAŁY.
PEŁNOŚĆ STRZAŁY
Weźmy bryły o takim samym polu podstawy i takiej samej długości, a różniące się wykładnikiem kształtu. Zauważmy, że bryły różnią się objętością: objętość stożka jest większa od objętości neiloidy, objętość praboloidy jest większa od objętości stożka, a objętość walca większa od objętości paraboloidy. Objętość brył rośnie ze spadkiem wartości wykładnika kształtu.
Pełność bryły jest to cecha bryły, której miernikiem jest wykładnik kształtu. Największą pełnością cechują się walec, dla którego wykładnik kształtu jest równy zero. Ze wzrostem wykładnika kształtu bryły maleje ich pełność.
ZBIEŻYSTOŚĆ STRZAŁY
Zbieżystość jest cechą kształtu bryły, której miernikiem jest różnica dwóch grubości z różnych miejsc bryły wyrażona w centymetrach, podzielona przez odległość między tymi miejscami, wyrażona w metrach.
Im większy jest parametr kształtu stożka, tym większy jest jego zbieżystość. Dla stożka o określony parametrze kształtu, zbieżystość jest jednakowa dla każdego odcinka bryły. Dla brył, których tworząca jest linią krzywą, zbieżystość zależy nie tylko od parametru i wykładnika kształtu, ale również od położenia odcinka na bryle. Dla brył o takim samym parametrze kształtu, których wykładnik kształtu zawarty jest w granicach 0*r*2,najmniejszą zbieżystością cechują się sekcja leżąca u podstawy bryły. Zbieżystość sekcji będzie rosła, gdy jej odległość od wierzchołka będzie malała.
Bryły o takim samym parametrze kształtu, dla których wykładnik kształtu r*2, mają największą zbieżystość dla odcinków leżących u podstawy. Zbieżystość sekcji będzie malała e spadkiem odległości sekcji od wierzchołka bryły.
Pełność i zbieżystość to dwie różne cechy kształtu. Bryły mogą się cechować taką samą pełnością, a ich zbieżystość może być różna.
SMUKŁOŚĆ STRZAŁY
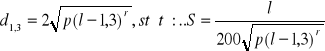
Smukłość jest to stosunek długości bryły wyrażonej w metrach do grubości wyrażonej w centymetrach. Najczęściej do określania smukłości przyjmuje się grubość bryły w odległości 1,3 m. licząc od jej podstawy. W przypadku strzały grubość tę nazywamy pierśnicą.
![]()
Bryły o tej samej długości i tum samym parametrze kształtu będą miały tym większą smukłość, im większa będzie ich pełność.
CECHY KSZTAŁTU POPRZECZNEGO STRZAŁY. ( STR. 32)
Przekrój poprzeczny bryły regularnej jest kołem. Skomplikowaną figurą jest natomiast przekrój poprzeczny strzały. Informują o tym cechy kształtu przekroju poprzecznego. Oceniają one stopień odbiegania przekroju poprzecznego strzały od przekroju kołowego.
Cechą kształtu przekroju poprzecznego jest kąt zawarty między największą i najmniejszą grubością przekroju (kąt równy lub mniejszy od 900). Gdyby kształt przekroju poprzecznego był zbliżony do kształtu elipsy, to wartość tego kąta powinna wynosić 900. Z badań Borowskiego wynika jednak, że średnia wartość tego kąta wynosi 700 i że kąt ten nie wykazuje żadne tendencji zmian z położeniem przekroju na strzale.
Inną cechą kształtu przekroju poprzecznego jest wartość kąta jaki tworzy kierunek północny z kierunkiem największej grubości ( kąt mierzony zgodnie z ruchem wskazówek zegara). Kąt ten daje informacje o kierunku wydłużenia przekroju poprzecznego. Borowski otrzymał średnią wartość równą 1070, czyli największa grubość występuje w kierunku Z-W, z odchyleniem Pd. Związane to jest prawdopodobnie z kierunkiem wiejących wiatrów.
CO TO JEST DOKŁADNOŚĆ TEORETYCZNA WZORÓW I W JAKO SPOSÓB PRZEPROWADZA SIĘ BADANIE DOKŁADNOŚCI TEORETYCZNEJ. Teoretyczną ocenę dokładności wzorów dendrometrycznych przeprowadza się na bryłach regularnych równaniu tworzącej y2=pxr.
DOKŁADNOŚĆ TEORETYCZNA WZORÓW: ŚRODKOWEGO PRZEKROJU, SMALIANA, HOSSFELDA.
Dokładność teoretyczna wzoru środkowego przekroju:
p
+10 9jioujoijuho
0 0 u=0,8
-10 u=0,4
-20 u=0,2
-30
-40
-50
-60 0 0,5 1 1,5 2 2,5 3 r u=0,0
Teoretyczna dokładność wzoru środkowego przekroju dla brył całkowitych i ściętych.
Dokładność teoretyczna wzoru Hossfelfa:
p
+5
0 1 2 3 r
-5
-10
-15
-20
-25
Dokładność teoretyczna wzoru Smaliana:
p
+100
+75
+50
+25
0 r
-25 0,5 1 1,5 2 2,5 3
-50
Teoretyczna dokładność wzoru Smaliana dla brył całkowietych.
BADANIE DOKŁADNOŚCI EMPIRYCZNEJ WZORÓW. ( STR. 45)
Ocenianie dokładności empirycznej przeprowadza się na drzewach i ich częściach ( strzałach, dłużycach, wyrzynkach itp.). Badanie polega na porównaniu miąższości określonej wzorem dendrometrycznym z miąższością rzeczywistą. Zwykle miąższość rzeczywistą określa się odpowiednim wzorem sekcyjnym.
DLACZEGO WZORY SEKCYJNE SĄ DOKŁADNIEJSZE OD WZORÓW ZWYKŁYCH. ( STR. 45)
Wzory sekcyjne są dokładniejsze od wzorów zwykłych z następujących przyczyn:
poszczególne sekcje obarczone są małymi błędami, o czym decyduje wysoka wartość stosunku średnicy górnej do dolnej. Natomiast błąd ostatniej sekcji, która jest bryłą całkowitą, nie wpływa w dużym stopniu na ogólny wynik z powodu małej miąższości tej sekcji.
Poszczególne sekcje cechują się różną pełnością, a tym samym otrzymuje się dla tych sekcji błędy różnych znaków. Przy sumowaniu miąższości sekcji błędy przynajmniej częściowo się redukują.
Przy stosowaniu wzorów sekcyjnych wykonuje się dużo pomiarów, a błędy pomiarowe mogą się w pewnym stopniu redukować.
Dokładność wzorów sekcyjnych będzie tym większa, i krótsza będzie długość sekcji. Wzrasta bowiem wówczas stosunek średnicy górnej do dolnej, który w głównej mierze decyduje o wielkości błędu. Dlatego przy badaniu dokładności wzorów sekcyjnych za miąższość rzeczywistą przyjmuje się tę która została określona wzorem sekcyjnym o krótszych sekcjach.
SPOSOBY WYZNACZANIA WYKŁADNIKA KSZTAŁTU I PARAMETRU DLA STRZAŁY.
Wykładnik kształtu
Poznanie pełności strzały wymaga określenia jej wykładnika kształtu. Wykładnik kształtu można określić następującymi metodami:
SPOSÓB GIERUSZYŃSKIEGO (na podstawie ilorazu grubości )
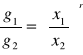
Weźmy dwa przekroje: g1 leżący w odległości x1 od wierzchołka, i g2 - leżący w odległości x2 od wierzchołka. Wykorzystując własność brył regularnych otrzymamy:
Pole przekroju poprzecznego brył regularnych jest równe polu koła, dlatego powyższy wzór można przedstawić w postaci
![]()
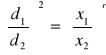
,gdzie d1 i d2 są średnicami kół. Po przekształceniu otrzymamy
do określania wykładnika kształtu zgodnie ze wzorem można brać grubości z różnych miejsc strzały. Gieruszyński proponuje uwzględnienie grubości z połowy długości strzały (d0,5l) i grubości z 1/10 długości licząc od podstawy strzały (d0,1l). Wzór przyjmuje postać:
![]()
SPOSÓB GROCHOWSKIEGO ( na podstawie położenia przekroju przeciętnego)
Przekrój przeciętny jest ilorazem miąższości strzały i jej długości. Oznaczamy odległość przekroju przeciętnego od podstawy strzały przez lx. Znając tę wielkość oraz długość strzały l, możemy określić wykładnik kształtu sposobem Grochowskiego.
![]()
SPOSÓB BRUCHWALDA (na podstawie długości części strzały o miąższości równej połowie miąższości całej strzały)
![]()
Określamy miąższość strzały (V) i następnie połowę miąższości. Znajdujemy długość odziomkowej części strzały (l0,5V), której miąższość jest równa połowie miąższości całej strzały. Między ilorazem długości części strzały i długością całej strzały a wykładnikiem kształtu zachodzi następujący związek:
Stąd;
![]()
PARAMETR KSZTAŁTU
określa się z tworzącej regularnych brył obrotowych:
![]()
Określanie parametru kształtu wymaga więc znajomości wykładnika kształtu, przekroju lub grubości na pewnej wysokości strzały oraz odległości przekroju od wierzchołka. Sposoby określania parametru kształtu związane są ze sposobami określania wykładnika kształtu.
SPOSÓB GIERUSZYŃSKIEGO
W sposobie tym wymagana jest znajomość grubości w połowie długości strzały (d0,5l) i grubości strzały na 1/10 jej długości (d0.1l). Parametr kształtu można więc określić wzorami:
![]()
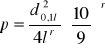
Lub
SPOSÓB GROCHOWSKIEGO
W sposobie Grochowskiego do określania wykładnika kształtu wymagana jest znajomość grubości odpowiadającej przekrojowi przeciętnemu (dx). Dlatego parametr kształtu określa się wzorem;
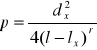
SPOSÓB BRUCHWALDA
Jeżeli wykładnik kształtu określony został sposobem bruchwalda to odpowiedni wzór na parametr kształtu ma postać:
![]()
POJĘCIE BRYŁY RÓWNOWAŻNEJ I CECHY WSPÓLNE DLA BRYŁY I STRZAŁY (STR. 30)
Bryła równoważna strzale jest bryłą regularną o równanie tworzącej y2= pxr, dla której parametr i wykładnik kształtu określony została podstawie cech strzały. Parametr i wykładnik kształtu bryły równoważnej przyjmujemy jako cechy danej strzały.
Cechy wspólne dla strzały i bryły równoważnej:
Jeżeli równanie tworzącej zostało określone sposobem Gieruszyńskiego, wówczas bryła równoważna będzie miała następujące cechy wspólne ze strzałą: długość, grubość w połowie długości i grubość na 1/10 długości licząc od podstawy bryły.
Przy zastosowaniu sposobu Grochowskiego strzała i bryła równoważna mają następujące cechy wspólne: długość oraz tej samej wielkości w tym samym miejscu położony przekrój przeciętny. Oznacza to jednocześnie że obie bryły będą miały taką samą miąższość (objętość )
Przy zastosowaniu sposobu Bruchwalda bryła równoważna i strzała będą miały następujące cechy wspólne: długość całkowitą i tej samej wielkości oraz w tym samym miejscu położony przekrój dzielący bryły na dwie części z których każda ma taką samą miąższość.
Z CZEGO WYNIKAJĄ RÓŻNORODNOŚCI MIĘDZY DOKŁADNOŚCIĄ TEORETYCZNĄ I EMPIRYCZNĄ WZORÓW DLA STRZAŁ
NIEDOSTOSOWANIE WZORU DO STRZAŁY W KIERUNKU PODŁUŻNYM Strzała jest bryłą o bardzo skomplikowanym kształcie przekroju podłużnego. Dlatego żaden z prostych wzorów dendrometrycznych nie będzie w sposób precyzyjny określał jej miąższości. Załóżmy, że krzywą morfologiczną można przedstawić równaniem tworzącej regularnych brył obrotowych y2=pxr . W taki wypadku błąd dla bryły całkowitej będzie zależał tylko od wykładnika kształtu , natomiast dla bryły ściętej zarówno od wykładnika kształtu jak i od stosunku średnicy górnej do dolnej.
Występowanie błędów o określonej wielkości i znaku można by było tłumaczyć tym, że dana strzała cechuje się określoną wartością wykładnika kształtu i stosunkiem średnicy górnej do dolnej . Oprócz tych cech o wielkości błędu dla strzały będzie decydował inny czynnik. Wynika on z rozbieżności między przebiegiem krzywej morfologicznej strzały i tworzącej równoważnej bryły obrotowej. Tworząca będzie pokrywała się z krzywą morfologiczną jedynie w nielicznych miejscach . Tworząca może przebiegać na zewnątrz lub wewnątrz krzywej morfologicznej (rys.). Dlatego błąd który wynika dla danej bryły z określonej wartości wykładnika kształtu i stosunku średnicy górnej do dolnej, może ulec zmniejszeniu lub zwiększeniu.
Tworząca bryły równoważnej
Krzywa morfologiczna strzały
11) NIEDOSTOSOWANIE WZORU DO KSZTAŁTU STRZAŁY W KIERUNKU POPRZECZNYM.
Przekrój poprzeczny strzały określa się najczęściej wzorem na pole koła. Tymczasem przekroje te odbiegają od kołowego. Świadczą o tym wyniki badań nad cechami kształtu przekroju poprzecznego strzały. Bardzo nieregularne są szczególnie przekroje podstawy strzały, co wynika z powstawania w dolnych partiach pnia zgrubień korzeniowych. Stosowanie wzoru na pole koła do określania przekroju poprzecznego strzały prowadzi do powstawania dużych błędów. Ma to szczególne znaczenie dla tych wzorów dendrometrycznych, które są oparte na prz3ekroju dolnym, a więc wzoru Smaliana i Newtona.
12) WPŁYW BŁĘDÓW POMIAROWYCH NA BŁĄD MIĄŻSZOŚCI DRZEWA. Przyczyną błędów określania miąższości strzał są błędy pomiarowe. Popełnia się je przy pomiarze długości, grubości i obwodu co wynika z niedokładności przyrządów i niedokładnego wykonywania pomiarów . szczególnej staranności wymaga pomiar grubości strzały, błędy bowiem popełniane przy tym pomiarze przy tym pomiarze mają duży wpływ na wynik miąższości. Przy wykonywaniu wielu pomiarów i matematycznym ich zaokrąglaniu błędy pomiarowe ulegają przynajmniej częściowej redukcji. Błędy powstałe na skutek zaokrąglenia wyników pomiaru grubości i długości tylko w dół prowadzą do otrzymywania wyłącznie błędów ujemnych, które przy masowych pomiarach nie redukują się.
Dokładność określania przeciętnej pierśnicy drzewostanu zależy w zasadzie od tych samych czynników , które decydują o dokładności określania przeciętnego przekroju drzewostanu. Są to czynniki: 1- błędy pomiarowe, 2- wielkość współczynnika zmienności pierśnicy drzew drzewostanu, 3- liczba drzew, na podstawie której określa się przeciętną pierśnicę, 4- liczba drzew drzewostanu.
13.WYJAŚNIĆ JAKIE MUSZĄ BYĆ SPEŁNIONE WARUNKI, ABY OKREŚLAJĄC MIĄŻSZOŚĆ DRZEWA LEŻĄCEGO ZWYKŁYMI WZORAMI NIE POPEŁNIĆ BŁĘDU.
Błędy jakie popełniamy przy pomiarze drzewa leżącego wynikają z:
PRZY POMIARZE DŁUGOŚCI :
niedokładności przyrządu ( złe wyskalowanie taśm parcianych)
niewłaściwego sposobu wykonania pomiaru lub niedokładnego wykonania pomiaru ( mierzymy zazwyczaj wzdłuż osi morfologicznej nie zaś wzdłuż osi strzały, niedokładny pomiar wynika z niestarannego przyłożenia taśmy, niestarannego odczytu, przesłyszenia się - jest to przyczyną błędów grubych
zaokrąglania wyników pomiarów ( przy zaokrąglaniu w dół maksymalny błąd wynosi pełną jednostkę zaokrąglenia , przy zaokrąglaniu matematycznym granicą jest połowa jednostki
b) PRZY POMIARZE GRUBOŚCI
Muszą być spełnione warunki średnicomierza:
ramiona powinny być prostopadłe do listwy i leżeć w jednej płaszczyźnie
długość ramion nie może być krótsza od połowy mierzonej grubości drzewa
ramię powinno przesuwać się łatwo po listwie
Aby poprawnie określić miąższość drzewa leżącego należy zwrócić
uwagę na punkty przytoczone powyżej i wyciągnąć odpowiednie wnioski.
14.SPOSOBY OKREŚLANIA MIĄŻSZOŚCI DRZEWA STOJĄCEGO.
a) TABLICAMI MIĄŻSZOŚCI
Dla poszcz. gat. na podstawie pierśnicy i wysokości (sosna dodatkowo do 80 lat i dla starszej)
Tabl. Grundnera, Schwappacha, t. Czuraja, Radwańskiego, Strzemeskiego, t. Radwańskiego.
b) wzorem Denzina
V=0,001d2
Zaletą wzoru - prostota, wadą mała dokł. (niezłe wyniki jedynie dla sosny o h około 30 m)
c)Określanie miąższości strzały i części strzały bez kory
Tablice Radwańskiego - podają grubość bez kory w różnych miejscach strzały oraz miąższość bez kory od podstawy do różnych wysokości - umożliwia to określenie miąższości bez kory części pnia z dowolnej wysokości na podst. pierśnicy w korze i wysokości drzewa
15.CO TO JEST BŁĄD TABLIC?
BŁĄD TABLIC - wynika z rozbieżności między liczbami kształtu użytymi do obliczenia miąższości tablicowych z rzeczywistymi l. ksz. badanych drzew. Dokładność tablic zależy od liczby cech wziętych pod uwagę oraz stopnia ich powiązania z pierśnicową liczbą kształtu, doboru ilości i jakości materiału empirycznego wziętego
do budowy tablic, jak również sposób ich budowy.
Dokł. nie jest duża (nawet pow. 100 % dla młodych drzew - lepsza dla d-stanów; błędy dla drzew redukują się).
Jeżeli wynik ma być dokładny może zachodzić konieczność wykonania podwójnej interpolacji - ze względu na pierśnicę i wysokość:
16.CO WPŁYWA NA WIELKOŚĆ BŁĘDÓW POPEŁNIONYCH PRZY OKREŚLANIU MIĄŻSZOŚCI DRZEWA STOJĄCEGO TABLICAMI MIĄŻSZOŚCI ?
Błąd przy określaniu pierśnicowego pola przekroju. Błąd instrumentów - klupy . Błąd wynikający z zaokrągleń.
BŁĄD TABLIC - wynika z rozbieżności między liczbami kształtu użytymi do obliczenia miąższości tablicowych z rzeczywistymi l. ksz. badanych drzew. Dokładność tablic zależy od liczby cech wziętych pod uwagę oraz stopnia ich powiązania z pierśnicową liczbą kształtu, doboru ilości i jakości materiału empirycznego wziętego
do budowy tablic, jak również sposób ich budowy.
Dokładność nie jest duża (nawet pow. 100 % dla młodych drzew - lepsza dla d-stanów; błędy dla drzew redukują się).
Jeżeli wynik ma być dokładny może zachodzić konieczność wykonania podwójnej interpolacji - ze względu na pierśnicę i wysokość:
17.LICZBY KSZTAŁTU: PIERŚNICOWA, WŁAŚCIWA, ABSOLUTNA.
PIERŚNICOWA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca o wysokości równej wysokości drzewa i polu podstawy równym pierśnicowemu polu przekroju drzewa:
WŁAŚCIWA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca, którego wysokość jest równa wysokości drzewa a pole podstawy polu przekroju drzewa na wysokości h/n:
n - dowolna liczba większa od jedności (najczęściej 10).
ABSOLUTNA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca o wysokości równej wysokości drzewa i o przekroju równym przekrojowi podstawy drzewa:
A. l. k. stanowi granicę, do której dąży w. l. k., gdy n dąży do nieskończoności.
Dla regularnych brył obrotowych o równaniu tworzącej y2 = pxr wzór na a. l. k. ma postać:
l. k. to teoretycznie miernik pełności (korelacja dodatnia z r) jednak praktycznie nieprzydatna - duża rozbieżności tworzącej bryły równoważnej z krzywą morfologiczną przy podstawie. Z tych samych powodów nieprzydatna do określania miąższości drzewa stojącego.
18.PIERŚNICOWE LICZBY KSZTAŁTU, PODAĆ DEFINICJE I PORÓWNAĆ ICH WIELKOŚCI.
PIERŚNICOWA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca o wysokości równej wysokości drzewa i polu podstawy równym pierśnicowemu polu przekroju drzewa:
Rodzaje liczb kształtu:
Pierśnicowe liczby kształtu strzały:
Pierśnicowa liczba kształtu grubizny drzewa:
Vg - miąższość grubizny strzały w korze wraz m miąższością grubizny gałęzi
Pierśnicowa liczba kształtu całego drzewa:
licznik - miąższość całego drzewa w korze.
Analiza wzoru na podstawie badań Głąbińskiego:
pierśnicowa liczba kształtu dla brył reg. zależy od wykładnika kształtu i wysokości.
taki sam wykładnik, różna wysokość - różna l. kształtu (mniejsza dla brył wyższych).
stała h (większa od 6,5 m), r rośnie w przedziale (0-3,5) - maleje l. kształtu.
stała h (w przedziale 2,1-6,5 m), r jak wyżej - l. k. najpierw maleje potem rośnie.
stała h (w przedziale 1,3-2,1 m), r jak wyżej - l. k. rośnie
Zmienność pierśnicowej liczby kształtu i jej zależność od niektórych cech drzewa
Zmienność p. l. k. dość duża (współczynnik zmienności dla d-stanów sosnowych 6-9 %).
Pierśnicowa liczba kształtu zależy od:
pierśnicy - na ogół drzewa grubsze mają mniejszą p. l. k. W d-stanach średnich
i starszych klas wieku związek słaby lub nieistotny, silniejszy w młodnikach sosnowych
i d-stanach świerkowych i jodłowych.pierśnicy (słabiej niż od pierśnicy) - na ogół drzewa wyższe mają mniejszą p. l. k.
W d-stanach średnich i starszych klas wieku związek nieistotny, silniejszy w młodnikach sosnowych i d-stanach świerkowych i jodłowych.% grubości kory na pierśnicy - w d-stanach sosnowych związek średniej mocy, słabszy dla gatunków o cienkiej korze (buk, świerk, jodła): większy procent - mniejsza p. l. k.
ilorazu q2 () - większy iloraz - większa p. l. k. (silny związek).
ZASTOSOWANIE PIERŚNICOWEJ LICZBY KSZTAŁTU
Podstawa opracowania systemu pomiaru lasu w praktyce i doświadczalnictwie:
miąższości drzewa i d-stanu, przyrostu miąższości drzewa i d-stanu.
pełności strzały (r można określić gdy oprócz f dane również h). Przydatność p. l. k.
do tego celu w d-stanach młodszych i starszych klas wieku mniejsza.
f3 < f g< f1 <f2<fd
19.POMIAROWO- SZACUNKOWE METODY OBLICZANIA POLA POWIERZCHNI OPISAĆ JEDNĄ.
Patrz skrypt z terenówek.
20.PROCENT PRZYROSTU MIĄŻSZOŚCI I DO CZEGO SŁUŻY.
Procent przyrostu miąższości jest miarą energii wzrostu,, informuje nas o stopniu wykorzystania powierzchni wzrostu przez drzewo i drzewostan . Procent przyrostu miąższości jest stosowany w budowie modeli służących do oceny sumarycznej produkcji . Służy on również do określenia procentu przyrostu miąższości . Procent przyrostu miąższości można określić wzorem na rachunek procentu składanego i wzorami na rachunek procentu zwykłego.
gdy przyrost odnosimy do wielkości końcowej ( wzór Brymanna)
b) gdy przyrost odnosimy do wielkości początkowej
c) wzór Presslera
gdzie:
Pv- procent przyrostu miąższości ( dla okresu rocznego)
V- miąższości dla końca okresu
v- miąższość dla początku okresu
n- długość okresu
Procent przyrostu miąższości można określić także z tablic. Jednak w tym przypadku należy wiedzieć jakim wzorem podany w tablicach procent przyrostu miąższości został określony.
21.METODA BOROWSKIEGO, OKREŚLENIE PRZYROSTU MIĄŻSZOŚCI.
Przyrost miąższości drzewostanu metodą Borowskiego można określić z iloczynu średniej wartości intensywności przyrostu miąższości (i) i pierśnicowego pola przekroju drzewostanu (G):
Pierśnicowe pole przekroju drzewostanu powinno się określać na podstawie pomiaru pierśnic wszystkich drzew . Intensywność przyrostu miąższości określa się na ściętych drzewach próbnych, a w zależności od sposobu pobierania tych drzew można wyróżnić warianty metod określania przyrostu miąższości drzewostanu .
Schemat metody:
Pomiar pierśnic drzew w odpowiednim odstopniowaniu i określenie pierśnicowego pola przekroju drzewostanu.
Zaplanowanie pewnej liczby drzew na podstawie której określi się średnią wartość intensywności przyrostu miąższości i przydzielenie jej proporcjonalnie do liczby drzew w stopniach pierśnicy
Sporządzenie krzywej wysokości i linii przyrostu pierśnic oraz określenie pożądanych wymiarów drzew próbnych
Wybranie drzew próbnych o pożądanych wymiarach cech pomocniczych
Zmierzenie pierśnicy wybranych drzew a po ich ścięciu określenie przyrostu miąższości każdego drzewa sposobem sekcyjnym.
Określenie średniej wartości intensywności przyrostu miąższości na podstawie drzew próbnych
Określenie przyrostu miąższości drzewostanu zgodnie z wzorem na górze
Istotą tej metody jest uwzględnienie przy wyborze drzew próbnych przyrostu pierśnicy. Jest to jedna z najdokładniejszych metod określania przyrostu miaższości.
22.OKREŚLANIE MIĄŻSZOŚCI DRZEWOSTANU ZA POMOCĄ DRZEW PRÓBNYCH METODĄ Z WYKORZYSTANIEM PIERŚNICY I GRUBOŚCI KORY.
W drzewostanie mierzymy pierśnice wszystkich drzew i sporządzamy krzywą wysokości . Na pewnej liczbie drzew mierzymy pierśnice i podwójną grubość kory na pierśnicy, po czym sporządzamy linię grubości kory. Przyjmujemy pewną liczbę drzew próbnych , którą rozkładamy proporcjonalnie do liczby drzew w stopniach pierśnicy . Wybieramy teraz takie drzewa, które dla określonej pierśnicy mają wysokość i grubość kory zbliżoną do wartości średnich odczytanych z wykresów dla danej pierśnicy. Drzewa ścinamy i określamy ich miąższość sposobem sekcyjnym. Miąższość drzewostanu określamy z iloczynu średniej wartości wysokości kształtu drzew próbnych i pierśnicowego pola przekroju drzewostanu .
Wzór na miąższość V= HF*G
23.OKREŚLENIE RÓWNANIA BRYŁY RÓWNOWAŻNEJ METODĄ BRUCHWALDA.
Określanie WYKŁADNIKA KSZTAŁTU na podstawie długości części strzały o miąższości równej połowie miąższości całej strzały (sposób
Bruchwalda).
SPOSOBY OKREŚLANIA PARAMETRU KSZTAŁTU:
sposób Bruchwalda
r - wykładnik kształtu określony sposobem Bruchwalda
BRYŁA RÓWNOWAŻNA STRZALE - bryła regularna o równaniu tworzącej y2 = pxr, dla której parametr i wykładnik kształtu określony został na podstawie cech strzały.
Parametr i wykładnik kształtu bryły równoważnej przyjmuje się jako cechy danej strzały.
Tworząca bryły równoważnej nie pokrywa się z krzywą morfologiczną strzały. Duże rozbieżności szczególnie w części dolnej i górnej brył (równanie y2 = pxr jest zbyt proste,
by odwzorować przebieg krzywej). Mniejsza rozbieżność między liniami występuje
w przypadku krótkich odcinków strzały.
Porównanie strzały i bryły równoważnej
sposób |
cechy wspólne strzały i bryły równoważnej |
|
|
Bruchwalda |
- długość |
Zestaw 1
Metody określania liczb kształtu dla drzewostanu przy uwzględnieniu stopnia grubości kory i pierśnicy.
Sposoby wyznaczania i cel przeciętnej wysokości drzewostanu i stopni grubości.
Gdzie i w jaki sposób wykorzystywane są związki pierśnicowej liczby kształtu z różnymi cechami.
Od czego zależy dobór metod wyznaczania miąższości za pomocą drzew próbnych ?
Do czego służą tablice miąższości i zasobności .
Co to jest stała krzywa wysokości- do czego służy?
Miąższość za pomocą drzew próbnych z uwzględnieniem podwójnej grubości kory.
Błąd średni w metodzie liczb kształtu.
Metody określania miąższości.
Do czego służą tabele IBL i Radwańskiego.
Zestaw 2
Kiedy dokładność określania miąższości będzie taka sama wzorem empirycznym z dokładnością teoretyczną.
Co trzeba pomierzyć aby obliczyć wykładnik kształtu metodą Grochowskiego ?
Co trzeba pomierzyć aby określić przyrost metodą Bruchwalda?
Dlaczego metoda Bruchwalda określona jest jako metoda właściwych liczb kształtu?
Metody określania miąższości drzewostanu za pomocą F2
Metody określania miąższości za pomocą tablic IBL
Do czego służą stałe linie liczb kształtu i stałe krzywe wysokości?
Strona 11 z 16
![]()
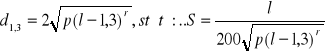
Smukłość bryły o długości l i pierśnicy d1,3 jest równa:
Dla brył regularnych
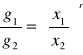
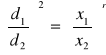
![]()
![]()
![]()
![]()
![]()
![]()
![]()
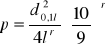
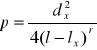
![]()
![]()
![]()
![]()
![]()
![]()
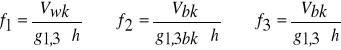
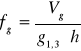
![]()
![]()
![]()
![]()
![]()
![]()
![]()
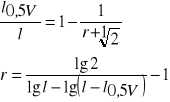
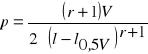
Wyszukiwarka
Podobne podstrony:
dendrochronologia
Lab Wypełnianie macierzy dendro meteo
Dendronized Polymers
dendrologia1, dendrologia 0001
wiecznie zielone, Studia, I rok, I rok, II semestr, Dendrologia
Dendrobium pielęgnacja storczyka
Dendro 2, LEŚNICTWO SGGW, MATERIAŁY LEŚNICTWO SGGW, od szatana, 2 rok
dendro ściąga
Ekspertyza dendrologiczna przykład
Dendrologia- pytania przykładowe- kolowium II, Moje studia na SGGW - Ogrodnictwo, Dendrologia
dendro 1, Studia, Dendrometria
cisy i jodły, Studia, I rok, I rok, II semestr, Dendrologia
dendro 3 ktoś
PROTOKOL Z CWICZEN Z DENDROMETR Nieznany
dendrologia1, dendrologia 0003
dendron
Egzamin z przedmiotu DENDROLOGIA, Studia, I rok, I rok, II semestr, Dendrologia
więcej podobnych podstron