1. Działy mechaniki, modele ciała stałego stosowane w mechanice.

Mechanika - nauka badająca ruch mechanicznego ciała, zarówno w stosunku do otoczenia, jak też w funkcji czasu. Mechanika ogólna bada ruch mechaniczny ciał stanowiących pewne uproszczenie myślowe ciał rzeczywistych

Mechanika ciała stałego - fizyka ciała stałego: mechanika ogólna (ciało stałe traktujemy jako punkt materialny - pomijamy rozmiar ale nie masę - . Bryła doskonale sztywna - pod wpływem obciążeń nie doznaje odkształceń. Mech. Ciała odkształconego (odkształcenie czysto sprężyste - teoria sprężystości, odkształcenia spręż. - plastyczne - teoria plastyczności.

Modele ciała:

• punkt materialny, jako punkt geometryczny obdarzony masą

• układ punktów materialnych

• ciało sztywne - odległość między dowolnymi punktami wewnątrz tego ciała jest stała ( niezależnie od sił wywieranych na to ciało)

2. Definicja, cechy, podział i jednostki sił.

Siła - wynik wzajemnego mechanicznego oddziaływania na siebie ciał. Oddział. to jest całkowicie określone, jeżeli jest znana jego wartość (moduł), kierunek, zwrot oraz punkt przyłożenia. Siła działająca na pewien punkt ciała stanowi wektor umiejscowiony.

Podział sił -

• Zewnętrzne (pochodzące od innych ciał): s. czynne( przy obciążeniach dąży do wprawiania ciała w ruch), s.bierne (reakcje, stanowią wynik oddziaływania więzów)

• wewn.: siły spójności, siły jednostkowe (naprężenia), siły napięcia

Wyróżniamy również siły: ciążenia, magnetyczne, elektryczne, reakcji - zewnętrzne bierne oddziaływujące na ciało.

F= m x a [ 1N= kg x m/s²] - siła skupiona, m - masa, a - przyspieszenie

q[ N/m] - siła ciągła na całej powierzchni, p=[N/m²] - obciążenie powierzchniowe

V= [N/mm³] - siła objętościowa

Jednostka siły: NIUTON - (N) - jest to siła która masie 1kg nadaje przyspieszenie 1m/s². Wielokrotności tej jednostki: dekaniuton - daN (1daN = 10N), meganiuton - MN (1MN = 10⁶N)

Układy sił - zbiór dowolnej liczby sił jednocześnie działających na rozpatrywane ciało.

Układ sił płaski - linie wszystkich sił leżą w jednej płaszczyźnie,

układ przestrzenny - nie leżą w jednej płaszczyźnie,

równoległe - kierunki działających sił nie przecinają się

zbieżne - linie działania wszystkich sił przecinają się w jednym punkcie

dowolne -m linie działania przecinają się w więcej niż w jednym punkcie

(rys)

3. Zasady statyki (aksjomaty)

Statyka opiera się na pewnej liczbie stwierdzeń poczynionych na podstawie obserwacji świata. Stwierdzenia te nazywamy aksjomatami (pewnikami) statyki

Aksjomat 1

Reguła równoległoboku dwie dowolne siły F₁ i F₂ przyłożone do jednego punktu można zastąpić siłą wypadkową W przyłożoną do tego punktu i przedstawioną jako wektor tego punktu będący przekątną równoległoboku zbudowanego na wektorach

(rys)

F w

F

szczególny przypadek:

1. ten sam zwrot i kierunek

2. zwrot o sile większej wartości

Aksjomat 2

Zasada równoważenia - dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy gdy działają wzdłuż jednej prostej , mają te same wartości liczbowe i są przeciwnie skierowane

(rys)

Aksjomat3

Zasada dla ciał sztywnych - działanie ukł. sił przyłożonych do ciała sztywnego nie ulegnie zmianie gdy do ciała tego dodamy bądź odejmiemy ukł. sił równoważących się, czyli tzw. ukł. zerowy

Dla ciała sztywnego punkt przyłożenia siły nie jest istotny. Każdą siłę działaj. Na ciało sztywne można dowolnie przesuwać wzdłuż linii jej działania. Dla ciał odkształcalnych zasada ta nie obowiązuje.

(rys)

Aksjomat4

Zasada zesztywnienia - równowaga sił działających na ciało odkształcalne nie ulegnie naruszeniu w skutek zesztywnienia tego ciała. Z zasady tej wynika, że zwiększenie sztywności ciała nie powoduje naruszenia jego równowagi. Natomiast zmniejszenie może ale nie musi naruszyć równowagi.

(rys)rozciąganie

(rys)ściskanie

Aksjomat5

Zas. działania i przeciwdziałania - każdemu działaniu towarzyszy równe co do wartości i przeciwnie skierowane wzdłuż tej samej prostej przeciwdziałanie.

Ciało nieswobodne - ciało z ograniczoną swobodą poruszania.

Więzy - warunki ograniczające swobodę poruszania się układu punktów materialnych lub ciał.

Siły reakcji - siły bierne, stanowią wynik oddziaływania więzów. Zależą one od warunków w jakich znajduje się dane ciało lub układ.

W miejscu stykania następuje oddziaływanie ciała na więzy i więzów na ciało.

(rys)

Aksjomat6

Zas. oswobodzenia więzów - każde ciało nieswobodne można myślowo oswobodzić od więzów zastępując przy tym ich działanie odpowiednimi reakcjami, dalej ciało można rozpatrywać już jako swobodne podlegające działaniu sił czynnych oraz sił reakcji więzów.

(rys)

4.Rzutowanie sił na osie ukł. współrzędnych.

Wartość rzutu jest dodatnia

Fx = AC ; AC/F = cosα ; AC = Fx = F x cosα ; Fx - rzut siły F na kierunek osi x

Fy - rzut siły F na kierunek osi y

Fy = BC = AD ; AD/F = cosβ ; AD= Fy= Fcosβ ; BC/F= sinα ; BC= Fy= Fsinα

(rys)

Szczególne przypadki:

1. α = 0^o; cosα= 1; Fx= F1= F; jeżeli siła jest równoległa do osi i ma tę samą wartość, to wartość rzutu równa się wartości siły

(rys)

2. α = 180^o; cosα= -1; Fx= -F; Fx= F(-1); Fx= -F

(rys)

3. α = 90^o; α = 270^o; jeżeli siła jest prostopadła do osi, to rzut siły równa się 0

-1≤ cosα ≤ 1 wartość rzutu nie może być większa od wartości siły

0< α< 90^o <cosα< 1

(rys)

Fx = Fcos120^o; cos120^o= -0,5; Fx= F(-0,5); Fx= -1/2F

Fx= -Fcosv; Fx= -Fcos60^o; Fx= -1/2F

(rys)

5.Moment siły względem punktu (bieguna). Moment główny układu sił

Momentem siły F względem punktu 0 - nazywamy wektor M_o, którego wartość bezwzględna równa się iloczynowi wartości liczbowej siły F i ramienia tej siły względem punktu 0.

Kierunek wektora momentu M_o jest prostopadły do płaszczyzny przechodzącej przez linię działania siły i biegun 0.

Zwrot wektora momentu wynika z reguły śruby o gwincie prawozwojnym.

Jednostka momentu- NIUTONOMETR

M_o= Fr [ Nm]; r - wektor, promień łączący punkt 0 z punktem zaczepienia siły F

(rys)obrotowe zachowanie ciała związane jest z momentem, nie z siłą

Moment = 0 gdy jeden z czynników = 0 (gdy nie ma ramienia albo siły)

Jeżeli biegun leży na linii działania siły to ramie działania siły względem tego bieguna = 0, bo moment po prostu zanika = 0.

Znak momentu dodatni M> 0 gdy siły obracają płaszczyznę w kierunku przeciwnym do obrotu wskazówek zegara.

Znak momentu ujemny M< 0 gdy siły obracają płaszczyznę w kierunku zgodnym do obrotu wskazówek zegara.

(rys)

Moment główny -(wypadkowy) dowolnego układu sił na płaszczyznę względem przyjętego bieguna 0 nazywamy algebraiczną sumę momentów poszczególnych sił tego układu względem tego samego bieguna 0.

TW. VARIGNONA (dla płaskiego układu sił zbieżnych) - moment względem dowolnego punktu 0 wypadkowej dwóch sił równy jest sumie algebraicznej momentów tych sił względem tegoż samego bieguna 0.

M_o= -Fr ; M_o= Fy x - Fx y

(rys)

6.Para sił i jej własności

Parą sił nazywamy układ dwóch sił o równej wartości, jednakowych kierunkach i przeciwnych zwrotach ( linie działania sil tworzących parę nie pokrywają się, ale są równoległe do siebie). Odległość linii działania pary nazywa się RAMIENIEM r.

Para sił nie posiada siły wypadkowej ale działanie sił tworzących parę nie równoważy się. Para sił działając na ciało materialne powoduje jego obrót. Para sił wytwarza moment.

Moment pary sił określający jej obrotowe działanie, jest WEKTOREM, którego wartość równa się iloczynowi wartości (M=Fr) jednej z sił tworzących parę i ramienia pary. Kierunek wektora momentu jest prostopadły do płaszczyzny przechodzącej prze linie działania pary. Zwrot tego wektora wynika z reguły o gwincie prawozwojnym

Przez dwie proste można poprowadzić tylko jedną płaszczyznę.

(rys)

Jeżeli wszystkie pary działają na jednej płaszczyźnie, to mają ten sam wektor momentu siły.

(rys)

Własności pary sił

1. Skutek działania momentu pary sił nie ulega zmianie jeżeli daną parę przeniesiemy w dowolne inne położenie w jej płaszczyźnie działania

(rys)

2. Skutek działania pary sił na ciało sztywne nie ulega zmianie jeżeli daną parę przeniesiemy w dowolne inne położenie na płaszczyźnie równoległej.

(rys)

3. Działanie pary sił nie ulega zmianie jeżeli proporcjonalnie powiększymy siły pary i pomniejszymy jej ramię bądź odwrotnie.

(rys)

4. Parę sił można zrównoważyć tylko drugą parą sił o równym co do wartości momencie lecz przeciwnego znaku (zwrocie).

(rys)

7.Składanie par sił leżących w jednej płaszczyźnie. Warunek równowagi par.

Gdy na ciało sztywne działa szereg par sił leżących w jednej płaszczyźnie, wówczas można je zastąpić jedną parą sił tzw. PARĄ WYPADKOWĄ.

Moment pary wypadkowej równy jest sumie algebraiczne momentów poszczególnych par składowych

M_w = M₁+ M₂+....+M_n= Σⁿ_i=1 Mi

Warunek równowagi W szczególnym przypadku sumując momenty par składowych można w rezultacie otrzymać zero. Mówimy wtedy, że rozważane pary znajdują się w równowadze. A zatem warunek równowagi par ma postać:

M₁+ M₂+ ...+M_n=Σⁿ_i=1 Mi = 0

8.Wyjaśnić pojęcia: ciało swobodne, ciało nieswobodne, stopnie swobody, więzy, reakcje więzów

Ciało swobodne - ciało pozbawione ograniczeń w poruszaniu się, posiada możliwość dowolnego ruchu w przestrzeni. Posiada 6 stopni swobody.

Dowolny ruch w przestrzeni - przesunięcie w trzech kierunkach x, y, z. 6 ruchów składowych, 3 możliwości ruchu względem osi x, y, z. , obroty wokół trzech współrzędnych.

(rys)

Ciało nieswobodne - ciało z ograniczoną swobodą poruszania

Stopnie swobody -

Więzy - warunki (najczęściej geometryczne) ograniczające swobodę poruszania się układu punktów materialnych (lub ciała).

R= - Q ; R - siła reakcji podłoża na ciało

W punktach gdzie ciało styka się z podłożem (więzami), następuje wzajemne oddziaływanie ciała na więzy i więzów na ciało

Siły którymi więzy oddziałują na ciało nieswobodne nazywamy SIŁAMI REAKCJI WIĘZÓW, bądź SIŁAMI ZEWNĘTRZNYMI BIERNYMI

Reakcje więzów - inaczej siły bierne, stanowią wynik oddziaływania więzów. Zależą one od warunków w jakich znajduje się dane ciało (lub układ)

9.Wyjaśnić jakie reakcje występują w najczęściej spotykanych więzach

Zasada oswobodzenia ciała z więzów:

(rys)

Siły reakcji więzów są przyłożone w punkcie styku ciała z więzami natomiast ich wartość, kierunek i zwrot zależą od działającego obciążenia zewnętrznego oraz od konstrukcji samych więzów. Pod względem konstrukcyjnym rozróżnia się następujące rodzaje więzów :

• więzy wiotkie (liny, łańcuchy, sznur...) W więzach wiotkich powstają siły których kierunek jest taki sam jak kierunek więzów (lin, łańcuchów...).Znany jest punkt przyłożenia, kierunek, zwrot, jedyna wielkość niewiadoma to wartość siły reakcji

(rys)

• podpora ruchoma, to więzy z jedną niewiadomą. Znany jest punkt przyłożenia, kierunek, zwrot, jedyna niewiadoma - wartość siły reakcji.

(rys)

• podparcie w kształcie uskoku: więzy z dwoma niewiadomymi. Nie znamy wartości sił V i H lub R i kątα

(rys)

• podpora przegubowa stała: również dwie niewiadome

(rys)

• utwierdzenie: więzy z trzema niewiadomymi tj. siła reakcji w jednym i drugim kierunku oraz moment

(rys)

10.Płaski zbieżny układ sił (definicja), wypadkowa takiego układu i sposoby jej wyznaczania (analityczny i wykreślny)

Płaski zbieżny (środkowy) układ sił - to taki układ gdzie wszystkie siły układu środkowego leżą w jednej płaszczyźnie

Wypadkowa układu - płaski dowolny dowolnej liczby sił zbieżnych przyłożonych do pewnego punktu 0 zastąpić można siłą wypadkową W równą sumie geometrycznej wszystkich sił tego układu i przyłożoną również do tego punktu 0 .

W = F₁ + F₂ + ... + F_n = Σⁿ_i=1 F_i

Suma geometryczna wartości składowych - metoda równoległoboku

(rys)

Metoda wieloboku

Suma rzutów dowolnej liczby sił zbieżnych na oś równa jest rzutowi siły wypadkowej tego układu na tę samą oś.

W_x = F_1x + F_2x + ...+ F_nx = Σⁿ_i=1 F_ix ; W_y = F_1y + F_2y + ...+ F_ny = Σⁿ_i=1 F_iy

W =

Cosα = Wx/W - kąt z osią poziomą ; sinα = Wy/W

(rys)

11.Warunki równowagi płaskiego zbieżnego układu sił (wykreślny i analityczny)

Aby siły zbieżne F₁, F₂, F₃...., działające w jednej płaszczyźnie znajdowały się w równowadze wielobok z nich zbudowany musi być wielobokiem zamkniętym co oznacza, że koniec ostatniego wektora w tym wieloboku musi pokrywać się z początkiem wektora pierwszego

=
1 +
2 + ...
n =
i =

W = - W_x = 0 ; - W_y = 0

Jeżeli siła wypadkowa W układu zbieżnego ma być równa 0, to zerować się również muszą oba rzuty tej wypadkowej na osie x i y prostokątnego układu współrzędnych.

Stąd analityczne warunki równowagi mają postać

W_x = F_1x + F_2x + ....F_nx = Σⁿ_i=1 F_ix = 0 ; W_y = F_1y + F_2y + ...F_ny = Σⁿ_i=1 F_iy = 0

Aby siły zbieżne leżące w jednej płaszczyźnie były w równowadze, sumy rzutów tych sił na obie osie układu współrzędnych muszą być równe 0.

Twierdzenie o trzech nierównoległych siłach - aby trzy nierównoległe do siebie siły działające na ciał sztywne były w równowadze, linie działania tych sił muszą przecinać się w jednym punkcie a same siły muszą tworzyć trójkąt zamknięty.

(rys)

12.Płaski dowolny układ sił - definicja, warunki równowagi układu

Płaskim układem sił - nazywamy układ w którym wszystkie siły leżą w jednej płaszczyźnie.

Dla płaskiego układu sił zbieżnych stosowane jest twierdzenie VARIGNONA: moment wypadkowej płaskiego układu sił zbieżnych względem dowolnego punktu płaszczyzny równa się algebraicznej sumie momentów poszczególnych sił względem tego punktu.

Redukcja obciążenia: M_B = F x r - para sił tworzy moment obrotowy F x r

Siłę F przyłożoną do dowolnego punktu A ciała sztywnego możemy zastąpić równą jej siłą przyłożoną do dowolnego punktu B tegoż ciała dodając jednocześnie parę sił o momencie równym momentowi danej siły F względem punktu B

Zasadę tą można uogólnić dla dowolnej liczby sił działających w jednej płaszczyźnie.

(rys)(wzór) z tyłu

Dowolny płaski układ sił przyłożonych do ciała sztywnego możemy zastąpić siłą wypadkową W przyłożoną do dowolnego punktu 0 tegoż ciała i równą sumie geometrycznej wszystkich sił tego układu oraz parą sił o momencie M₀ równą sumie algebraicznej momentów wszystkich sił tego układu względem bieguna redukcji 0.

Siłę W nazywamy wektorem głównym tego układu sił, natomiast moment M₀ nazywamy momentem głównym względem bieguna redukcji 0.

Warunki równowagi płaskiego dowolnego układu sił: aby dowolny układ sił o liniach działania leżących w jednej płaszczyźnie był w równowadze, wektor główny tego układu oraz moment główny tego układu muszą być równe zeru.

Warunek wektorowy (geometryczny) -
= Σⁿ_i=1
=
: F_1x + F_2x + ...F_nx = 0

F_1y + F_2y + ...F_ny = 0

Warunek algebraiczny - M₀ = Σⁿ_i=1 M_io = 0

Spełnienie warunku geometrycznego jest możliwe tylko wtedy, gdy zerować się będą rzuty wszystkich sum algebraicznych tego układu.

Trzy algebraiczne warunki równowagi

F_1x +F_2x + ...F_nx = ΣF_ix = 0 - suma rzutów wszystkich sił na kierunek poziomy osi x

F_1y + F_2y +.. F_ny = ΣF_iy = 0 - suma rzutów wszystkich sił na kierunek pionowy

M₀ = M₀₁ + M₀₂ + ..M_0n = Σⁿ_i=1 M_0i = 0 - suma momentów dowolnego punktu względem punktu 0

13.Płaski układ sił równoległych - definicja, wartość i położenie siły wypadkowej, warunki równowagi układu

P. ukł, sił równol. - układ sił leżących w jednej płaszczyźnie, gdzie linie tych sił nie przecinają się

(rys)

Wektor wypadkowy płaskiego układu sił równoległych równa się sumie algebraicznej poszczególnych sił tego układu

W =Σⁿ_i=1 F_i

(rys)

Położenie siły wypadkowej układu równoległego wyznacza się z warunku, że moment siły wypadkowej równy jest sumie algebraicznej momentów wszystkich sił tego układu względem dowolnego punktu 0.

(wzór)

Warunki równowagi płaskiego układu sił równoległych: są dwa konieczne warunki do spełnienia aby płaski układ sił równoległych znalazł się w równowadze:

1. zerowanie się siły wypadkowej układu W =Σⁿ_i=1 F₁ =0

2. suma algebraiczna momentów wszystkich sił tego układu względem dowolnego punktu zero ma być równa zero Σⁿ_i=1 M_i0 = Σⁿ_i=1 F_ixi = 0.

Twierdzenie VARIGNONA jest również słuszne dla sił równoległych. Stosując je można np. określić położenie wypadkowej dwóch sił równoległych.

Dla sił równol. o zwrotach zgodnych - wartość wypadkowej jest równa sumie wartości sił składowych, zwrot odpowiada zwrotowi sił składowych.

Linia działania wypadkowej przechodzi między liniami działania sil składowych w odległościach od nich odwrotnie proporcjonalnych do wartości sił składowych.

Dla sił równol. o zwrotach przeciwnych - wartość wypadkowej jest równa różnicy wartości sil składowych, zaś zwrot odpowiada zwrotowi siły o

wartości większej. Linia działania wypadkowej przebiega poza liniami działania sił składowych w odległościach od nich odwrotnie proporcjonalnych do wartości sil składowych.

14.Środek ciężkości ciała (definicja), określenie współrzędnych środka ciężkości figury płaskiej

Środek ciężkości - to miejsce przecięcia osi symetrii, gdy jedna oś symetrii nie musi leżeć w punkcie materialnym ciała. Jest to punkt, w którym zaczepiona jest siła ciężkości całego ciała.

Ciężar ciała

- wypadkowa równoległego przestrzennego układu sił

- suma sił ciężkości poszczególnych części ciała

Współrzędne środka:

- dla figur

- dla brył

15.Wyjaśnić, jak położenie środka ciężkości ciała wpływa na charakter równowagi ciała nieswobodnego.

Jeżeli ciało nieswobodne podparte zostanie powyżej środka ciężkości, jest w stanie równowagi stałej. Powraca do pierwotnego położenia. Po jego wychyleniu ze stanu równowagi, pojawia się para sił, która sprowadza je z powrotem do stanu równowagi. (rys a)

Ciało znajduje się w stanie równowagi chwiejnej, gdy jest podparte poniżej środka ciężkości (rys b)

Gdy ciało jest podparte w środku ciężkości to powstaje para sił, która nie dąży do obrotu tego ciała. Ciało znajduje się w stanie równowagi obojętnej (rys c)

16.Wyjaśnić co to jest tarcie ślizgowe (statyczne, kinematyczne), podać i objaśnić wzór na siłę tarcia. Co to jest współczynnik tarcia ślizgowego i od czego zależy.

Przy wzajemnym przesuwaniu dwóch ciał po sobie występują siły tarcia starające się nie dopuścić do tego przesunięcia. Jeżeli do ciała spoczywającego na poziomej powierzchni, przyłożymy siłę poziomą F, to podłoże oprócz reakcji pionowej N = G wywrze na ciało poziome oddziaływanie T zwane siłą tarcia.

Siła T jest równa co do wartości sile czynnej F, nie może jednak przekroczyć pewnej wartości maksymalnej, którą osiąga w granicznym położeniu równowagi.

(rys)

T₁ - opór jaki powstaje przy próbie przesunięcia ciała jedno o drugie

Siła tarcia statycznego - T = Nμ ; T = N tgς ; tgς = ц - współczynnik tarcia

T_gr - siła tarcia statycznego, największa siła oporu jaką trzeba pokonać przy próbie wyprowadzenia ciała ze spoczynku

Siła tarcia kinematycznego - T_k = N цk Tarcie kinematyczne - tarcie jakie zachodzi między ciałami znajdującymi się w ruchu

Siła tarcia kinematycznego < siły tarcia statycznego T_k < T

Współczynnik tarcia kinematycznego < współczynnika tarcia statycznego ц_k < ц

Ц - Współczynnik tarcia ślizgowego zależy od właściwości trących się materiałów, stanu powierzchni materiałów (chropowatości), od smarowania (smar obniża współczynnik tarcia), od tego czy tarcie kinematyczne czy statyczne, natomiast praktycznie nie zależy od pola powierzchni styku ciał

17.Wymienić podstawowe rodzaje prostych obciążeń, sprecyzować kiedy one występują

Rodzaje prostych obciążeń: siły wewnętrzne (napięcia i naprężenia)

W zależności od sposobu przyłożenia obciążenia zewnętrznego w wytrzymałości materiałów spotyka się 5 przypadków prostych obciążeń:

• ROZCIĄGANIE : kiedy przyłożymy układ sił działających wzdłuż osi pręta, a siły te są przeciwnie do siebie zwrócone. Warunek wytrzymałościowy: б= P/A
  k_r , k_r - naprężenia dopuszczalne, δ -naprężenie w poprzecznym przekroju pręta, A - pole przekroju poprzecznego pręta

(rys)

• ŚCISKANIE : występują naprężenia tylko normalne. Warunek wytrzym.

б = P/A
k_c

• ŚCINANIE : naprężenia styczne
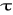
  _wy występujące tylko w płaszczyźnie tego przekroju

(rys)

• SKRĘCANIE : dwie pary sił działających na płaszczyznach prostopadłych na przeciwległych końcach o tych samych momentach, lecz różnych zwrotach

Wyst. Tu naprężenia styczne
_wz

(rys)

ZGINANIE : wyst. Gdy belka jest poddana parze sił leżących na osi belki i prostopadle działające. Powstaje siła poprzeczna (tnąca), wewnętrzny moment zginający wywołuje naprężenia ściskające i rozciągające. Naprężenia styczne są wywoływane, to naprężenia normalne.

(rys)

18.Podać definicję naprężenia normalnego i stycznego. Jednostki naprężenia.

Naprężenie w danym ounkcie przekroju można rozłożyć na składową normalną б (naprężenie normalne), i składową styczną
(naprężenie styczne)

Naprężenia normalne - (kierunek prostopadły do płaszczyzny przekroju)

(wzór)

Naprężenia styczne -
_wz (wzór)

Jednostki naprężenia : podstawową jednostką naprężenia jest paskal (Pa), tzn. jeden niuton na metr kwadratowy : 1Pa = 1N/m² [б ,
]. Stosuje się również krotność tej jednostki - megapaskal (MPa) 1Mpa = 10⁶ Pa = 10⁶ N/m² = 1MN/m²

10⁶ N/m² = 10⁶ N/10⁶ mm² =

19.Podać i objaśnić prawo Hooke'a przy rozciąganiu (ściskaniu). Zasada de Saint Venanta.

Hooke'a prawo, prawo określające zależność między siłą odkształcającą a odkształceniem dla ciała sprężystego (w granicy sprężystości).“Odkształcenie jest wprost proporcjonalne do działającego naprężenia i odwrotnie proporcjonalne do stałej naprężenia”. Dla pręta o długości l ściskanego (rozciąganego) siłą F działającą równolegle do osi długiej pręta, prawo Hooke'a wyraża się wzorem: l = Fl/sE, gdzie: l - wydłużenie, s - pole przekroju poprzecznego pręta, E - moduł Younga (moduł sprężystości). W ogólności prawo Hooke'a ma postać prawa tensorowego, o 21 stałych elastycznych.

20.Scharakteryzować odkształcenia wzdłużne i poprzeczne rozciąganego i ściskanego pręta. Liczba Poissona.

Poissona współczynnik, wartość bezwzględna stosunku odkształcenia poprzecznegoE _y względem wydłużeniaE _x ciała: µ**= IE**E*I

-stała materiełowa, charakteryzuje skłonność materiałów do odkształcania się w kierunku poprzecznym w stosunku do działającego obciążenia. Im liczba Poissona większa tym większe odkształcenie (jednak nie większe niż 0-0,5).

21.Narysować i omówić wykres rozciągania dla mat. plastycznych i kruchych.

Dla materiałów plastycznych zwykle wyraźnie zaznacza się granica plastyczności Qr¹ przy obciążeniu Ppl

Odkształ.

plastyczne

p

Odkształcenie zerwanie

sprężyste

P P

pl

P -oznaczono największą wartość siły podczas rozciągania, a przez Pz obciążenie, przy którym próbka uległa zerwaniu.

Natomiast dla materiałów kruchych za podstawe do wyznaczania kr służy doraźna wytrzymaość na rozciąganie Rr, obliczona z maksymalnej siły rozciągającej P i pola pierwotnego przekroju próbki A

2 R 1. bez wyraźnej granicy plastyczności

. 1 R 2. z zaznaczonym przybliżonym

określeniem umownej granicy

plastyczności oraz wykres dla

materiału kruchego

22.Wyjaśnić pojęcia: naprężenie dopuszczalne, współczynnik bezpieczeństwa- podać sposób ich wyznaczania.

a)naprężenie dopuszczalne: poziom naprężeń bezpiecznych; to takie naprężenie, które konstrukcja może bezpiecznie przenieść; naprężenie to nie może przekraczać granicy plastyczności; nie można dopuścić do płynięcia materiału. Rozróżniamy naprężenia dopuszczalne na: rozciąganie kr, ściskanie kc, ścinanie kt, skręcanie ks, zginanie kg. Naprężenie wyznaczamy z wzoru:

kr = Re / ne -gdzie Re- to granica plastyczności materiału, ne- to współczynnik bezpieczeństwa.

b)współczynnik bezpieczeństwa- w jego wartości ukryty jest współczynnik charakteryzujący zmianę własności fizycznej lub umownej granicy plastyczności i wytrzymałości doraźnej w zależności od wielkości przekroju przedmiotu. Wartości granicy plastyczności mogą ulegać obniżeniu wraz ze wzrostem wymiarów przedmiotu. W związku z tym przyjmuje się zwykle ostateczny współczynnik bezpieczeństwa jako:

Xq = δq γq -gdzie γq- określa wpływ wymiarów przedmiotu- najczęściej jednak określa się go jako γq=1;można jedynie mówić o wpływie czynników technologicznych na wartości Q1 i R1 i z nimi związanych niejednorodności materiałów; δq- jest tzw. rzeczywistym współczynnikiem bezpieczeństwa a jego sprawdzenie określa związek:

δq = σn / γq gdzie σn- jest największym naprężeniem nominalnym w najbardziej niebezpiecznym przekroje elementu; wartość δq w zależności od warunków pracy wynosi od 1,2 - 1,5.

Czynniki wpływające na dobór współczynnika bezpieczeństwa:

-rodzaj przeznaczenia;

-dokładność metod obliczeniowych;

-czas i warunki pracy (np.:korozja);

-jednorodność materiału;

-dynamika obciążenia;

-naprężenia własne.

23.Podać warunki wytrzymałościowe na rozciąganie i ściskanie, omówić sposoby korzystania z nich. W przypadku osiowego rozciągana pręta siłami N przyłożonymi do jego końców siła wewnętrzna w poprzecznym przekroju pręta jest równa N i podstawowy warunek wytrzymałości ma postać

Przy rozciąganiu б=NIAk (kiedy przyłożymy układ sił działający wzdłuż osi pręta, a siły te są przeciwne do siebie zwrócone. Warunek wytrzymałościowy)

k-naprężenia dopuszczalne na rozciąganie

σ- naprężenie w poprzecznym przekroju pręta

A- pole przekroju poprzecznego pręta

N- stała siła osiowa

Przy ścinaniu б = NIAk ( występują naprężenia tylko normalne)

k-naprężenia dopuszczalne na rozciąganie

Warunek ten umożliwia dobór wielokrotności obciążenia oraz określenie przekroju materiału

Warunek równowagi (H, V, N) = f(F)

-suma rzutów wszystkich sił na x :∑ Fx = 0, -H- N cosб= 0

-suma rzutów sił na kierunek pionowy: ∑ Fy = 0, V+N sinб -F = 0

-suma momentów względem punktu obrotu belki: ∑ Mo =0, -Fa+Nb sinб=0, sinб=r/b, r=bsinб

Z warunków wytrzymałościowych korzystać w celu obliczenia np. pola przekroju preta, naprężenia w przekroju poprzecznym, sprwdzić warunki wytrzymałościowe, obliczyć współczynnik bezpieczeństwa, siłę przy znanym przyłożeniu (skrucejniu) względnym, obliczyć wydłużenie pręta.

24.Momenty bezwładności figury płaskiej (osiowy i biegunowy)- definicja, własności, jednostki.

Moment bezwładności figury równy jest sumie dwóch osiowych momentów bezwładnych tej figury liczony względem dwóch wzajemnie prostopadłych osi przecinających się w tym biegunie.

J=+

Moment bez. Figury zależy od wielkości pola tej figury, al. Przede wszystkim od położenia tej figury w stosunku do osi względem której bezwładności ten moment liczymy. Im blizej osi leży biegun tym mocniejszy jest bezwładności.

Spośród wszystkich równoległych do siebie osi największy moment bez, jest jeśli liczymy go względem osi przechodzącej przez ciężkości figury.

Moment bez, liczony względem osi przechodzących przez środek ciężkości figury nazywamy środkowym albo centralnymi momentami bezwładności

Każda figura posiada nieskończenie wiele środkowych momentów bezwładności ale tylko dwa z pośród nich są głównymi i centralnymi.

Jeżeli figura posiada przynajmniej jedną oś symetrii to głównie centralne momenty bezwładności tej figury są to momenty liczone względem dwóch wzajemnie prostopadłych osi środkowych, z których przynajmniej jedna jest osią symetrii.

25.Scharakteryzuj własności mechaniczne materiału- wytrzymałość, twardość, udarność.

-Wytrzymałość mechaniczna, wartość graniczna naprężeń, jakie są w stanie zrównoważyć siły wewnętrzne. Zależy głównie od rozkładu uszkodzeń struktury ciała i stanu naprężeń wewnętrznych. Przy braku uszkodzeń strukturalnych wytrzymałość mechaniczna danego materiału może osiągać wartość 0,1 modułu Younga, praktycznie jest o dwa-trzy rzędy wielkości mniejsza. Younga moduł, podłużny moduł sprężystości, współczynnik sprężystości wzdłużnej, E, wielkość charakteryzująca sprężystość danego ciała.
E = Ο/E, gdzie: Õ- naprężenie normalne, E- względne wydłużenie ciała. Odwrotność modułu Younga α= 1/E nazywana jest współczynnikiem wydłużenia. Nazwa upamiętnia T. Younga.

-Twardość, własność ciał stałych polegająca na stawianiu oporu odkształceniom plastycznym przy lokalnym oddziaływaniu nacisku na ich powierzchni, wywieranego przez inne, twardsze ciało. Twardość jest cechą umowną, umożliwiającą porównywanie odporności na uszkodzenia powierzchni różnych materiałów. Powszechnie stosuje się kilka metod badania twardości (głównie metali).

W metodach Brinella, Rockwella, Vickersa mierzy się odpowiednie wymiary odcisków w badanym materiale, powstałe w wyniku wgniecenia wgłębnika (kulki stalowej lub z węglików spiekanych w metodzie Brinella, stożka diamentowego lub hartowanej kulki w metodzie Rockwella, diamentu w kształcie piramidy w metodzie Vickersa).

-Udarność, własność mechaniczna wyrażająca się odpornością materiału na pęknięcie przy uderzeniu. Do prób udarności używa się znormalizowanych próbek materiałów z nacięciem (w kształcie U lub V), które, oparte na podporach, uderzane są młotem wahadłowym po przeciwnej stronie nacięcia. Udarność obliczana jest jako stosunek energii zużytej na złamanie próbki do pola pierwotnego przekroju próbki w miejscu przełamania. Nowoczesne młoty udarnościowe do prób udarności wyposażane są w specjalne urządzenia różnicowe, pozwalające na bezpośredni odczyt ze skali wartości energii wykorzystanej do złamania próbki.

26.Wymienić i scharakteryzować stałe materiałowe (E, v, G).

E- stała materiałowa zwana współczynnikiem sprężystości wzdłużnej materiału (modułem Younga) w MPa, (stal 2.17x100000 MPa )

G- stała materiałowa zwana współczynnikiem sprężystości poprzecznej materiału lub modułem Kirchhoffa w Mpa G=E/2(1+v) (charakteryzuje odporność na odkształcenie postaciowe) dla stali 8x10000 Mpa)

V- stała materiałowa zwana współczynnikiem przewężenia poprzecznego (współczynnikiem Poissona) (v0.5) charakteryzuje skłonność materiałów do odkształcenia się w kierunku poprzecznym w stosunku do działającego obciążenia

27.Skręcqanie prętów o przekroju kołowym- założenia, odkształcenia, rozkład naprężeń w przekroju.

Skręcanie zachodzi gdy dołożymy w płaszczyznach prostopadłych 2 pary sił o równych wartościach lecz przeciwnych znakach.

Naprężenie: .................(naprężenie, odkształcenie, stała materiaowa) G=E/2(1+ϒ)

Prawo Hooke,a na stręcanie..................(moduł odkształcenia postaciowego ......jest wprost proporcjonalny do naprężenia.......i odrotnie proporcjonalny do stałej materiaowej G.

Odkształcenia- przekroje poprzeczne kołowe przed odkształceniem postają kołowymi , doznają jedynie obrotu w okól osi pręta,- promień przekroju obraca się wraz z tym przekrojem pozostając prostoliniowym,- linie tworzące pręta nie zmieniają swojej długości ( nie zmieniają się wymiary długościowe)

Rozkład naprężeń stycznych wzdłuż promienia pręta

.......................................................Wartość naprężeń w dowolnym punkcie przedmiotu...........................................................

Msw- moment skręcający wewnętrzny

Wo- wskaźnik wytrzymałości przekroju kołowego na skręcanie

Io- biegunowy moment bezwładności przekroju

28.Podać warunek wytrzymałościowy na skręcanie, omówić sposoby korzystania z niego.

Warunek wytrzymałości na skręcanie max=Msw/Wo k,

k- naprężenia dopuszczalne na skręcanie

wartości naprężeń w dowolnym punkcie przemiotu:

Msw -moment skręcający wewnętrzny; Wo- wskaźnik wytrzymałości przekroju kołowegona skręcanie, Io- biegunowy moment bezwładności przekroju

Wewnętrzny moment skręcający

Moment skręcający Ms [Nm]=9550P/n[kM/(obr/min)]

Ms[Gm]=71620P/n [kM/(obr/min)],M1-M2+Msw=M2-M1 Moment skręcający w przekroju skręcanego pręta oblicza się jako algebraiczną sumę momentów par równoległych do przekroju i działających na pręt z jednej strony tego przekroju.

29.Podać i omówić wzór na kąt skręcania przekroju kołowego pręta. Wyjaśnić co to jest sztywność skręcania i od czego zależy.

Kąt skręcania- (lub kat przekroju poprzecznego)-jest miarą sztywności pręta skręcanego)

,jest większy im silniekszy jest moment Ms, jest odwrotnie proporcjonalny do stałej materiałowej (zależy od rodzaju materiału) i momentu bezwładności

Powierzchnie zewnętrzne doznają wszystkich odkształceń

(wzór)

Msw- moment skręcający wewnętrzny

Io- biegunowy moment bezwładności przekroju

Sztywnośc skręcania- miarą sztywności pręta skręcanego jest kąt skręcania, Glo (G- stała sprężystości poprzecznej materiału w N/m², Io- geometryczna charakterystyka przekroju skręcanego pręta dla przekroju kołowego równa biegunowymi momentowi bezwładności w m

Sztywność skręcania zależy od wskaźnika wytrzymałości przekroju na skręcanie Wo

30.Wymienić rodzaje zginanych belek, omówić odkształcenia podłużnych włókien, rozkład naprężeń normalnych w przekroju belki (wykres i wzór z objaśnieniem).

Rodzaje belek

Odkształcenia belek - zarówno siła poprzeczna (T) jak i moment zginający Mg wywołują w przekroju belki pewien stan naprężenia. Moment zginający wywołuje w przekroju belki naprężenia normalne , a efektem ich działania jest wydłużenie jednych i skrócenie innych podłużnych włókien belki (rozkład naprężeń)

31.Wyjaśnić jakie obciążenia wewnętrzne występują w przekrojach zginanych belek, podać ich definicje i umowy dotyczące znaków.

W przekrojach zginanych belek wystepują dowolnego rodzaju obciążenia wewnętrzne i siły poprzeczne i moment zginający (gnący). Sła poprzeczna w rozpatrywaniu przekroju belki jest to algebraiczna suma siła suma sił prostopadłych do osi belki i działających na rozpatrywaną część belki.

Przy wyznaczaniu siły poprzecznej w przekroju belki ze znakiem plus uwzględniamy te siły wewnętrzne, które dążą do obrotu rozpatrywanej części belki w strone zgodną z ruchem wskazówek zegara, zaś ze znakiem minus w drugą stronę odwrotnie niż w momentach)

Moment zginający w przekroju belki jest to algebraiczna suma momentów tworzonych przez obciążenia zewnętrzne działające na rozpatrywaną część belki. Przy sumowaniu tych elementów ze znakiem plus, bierzemy te momenty, które wyginają belke wypukłością ku dołowi. Ze znakiem minus , te które wyginają belkę wypukłością ku górze .

Zarówno siła poprzeczna (T) jak i moment zginający Mg wywołują w przekroju belki pewien stan naprężenia. Moment zginający wywołuje w przekroju belki pewien tan naprężenia normalne, a efektem ich działania jest wydłużenie jednych i skrócenie innych podłużnych włókien belki.

Naprężenia te decydują przede wszystkim o wytrzymałości zginanej belki. Naprężenia styczne wywołane działaniem siły poprzecznej nie są na ogół duże i w przybliżonych obliczeniach zginanych belek można je pominąć.

32.Wyjaśnić co to jest przekrój niebezpieczny belki, podać i wyjaśnić warunek wytrzymałościowy na zginanie, omówić sposoby korzystania z niego.

G(y)= [Mg(x)/Iz](y), Gmax= Mg/Iż(y)

Wskaźnik wytrzymałości na zginani(Wz) Wz=z/y

Warunek wytrzymałości na zginanie б=Mg/Wz ≤ k - naprężenie maksymalne,

Wz =Iz/ y -wskaźnik wytrzymałości na zginanie m,

k-naprężenie dopuzczalne na zginanie

33.Wyjaśnić co to jest linia ugięcia belki, scharakteryzować przemieszczenia przekroju poprzecznego belki, co to jest sztywność zginania.

Linia ugięcia belki - jest to zakrzywiona os belki

Sztywność zginania- E Iż (iloczyn stałej materiałowej zwanej współczynnikiem spręzystości wzdłużnej materału- moduł Younga - Mpa i modułu bezwładności.)

6

6

---