Wykład 1
1. Podstawowe pojęcia.
Co jest przedmiotem prognozowania? Budowanie prognoz, np. prognoz gospodarczych, społecznych, politycznych, rozwoju całego świata, rozwoju gminy, lokalnej społeczności, rozwoju branży, firmy…
Co rozumiemy przez prognozę danego zjawiska? - wskazanie najbardziej prawdopodobnej drogi rozwoju tego zjawiska w oparciu o naszą wiedzę, dotychczasowy przebieg zjawiska, wiedzę o obecnym stanie zjawiska.
Prognoza to wypowiedź o przyszłości. Nie wiemy jaka będzie przyszłość. Prognoza jest efektem prognozowania.
Oszacowanie to wypowiedź o przeszłości lub teraźniejszości Dotyczy parametrów, których dokładnych wielkości nie znamy. Oszacowanie to wynik szacowania.
Wypowiedzi na temat przyszłości - przewidywanie przyszłości, możemy podzielić na:
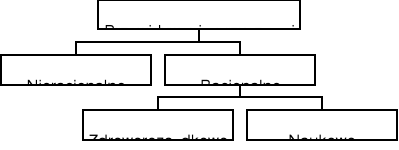
(Cieślak, 1997, Prognozowanie gospodarcze)
Przyjmujemy, że prognozowanie:
to działania racjonalne posługujące się metodami naukowymi,
odnosi się do określonej, zazwyczaj niezbyt odległej przyszłości.
Prognoza:
jest budowana z wykorzystaniem nauki,
odnosi się do nieodległej przyszłości,
jest empirycznie weryfikowalna,
jest prawdziwa z dużym prawdopodobieństwem.
My będziemy zajmować się tylko prognozami ekonometrycznymi, budowanymi na podstawie modeli ekonometrycznych.
Termin prognoza bywa też używany w nieco innym znaczeniu - bez zakładania, że jest to wypowiedź o przyszłości, np. prognoza zawartości złoża przed przystąpieniem do eksploatacji. My powiedzielibyśmy szacowanie wielkości złoża.
Prognoza pogody na jutro mówi jakie, z dużym prawdopodobieństwem, będą warunki pogodowe następnego dnia. Prognoza pogody ma charakter bezwarunkowy.
Prognoza zjawisk ekonomicznych ma często charakter warunkowy. Jeśli będą spełnione pewne warunki, zrealizowane pewne działania, to nastąpi określone zjawisko ekonomiczne.
Funkcje prognozy:
wspomagająca podjęcie decyzji mikro i makroekonomicznych (przygotowująca, preparacyjna);
aktywizująca, wspomagająca podjęcie działań aktywizujących lub przeciwstawiających się;
informacyjna, uprzedzenie, poinformowanie o mogących nastąpić zmianach, skutkach działań.
Konstruowanie prognozy jest wskazane gdy:
horyzont czasowy jest krótki,
zmiany prognozowanej wielkości są powolne,
prognozowane wielkości mają głównie autonomiczny charakter, mało zależą od arbitralnych decyzji,
jest duża inercja (bezwładność) prognozowanej zmiennej.
Główne zastosowanie w gospodarce to prognozowanie:
wielkości, których nie da się zaplanować,
wskaźników techniczno-ekonomicznych,
finansowe,
ścieżek rozwoju,
efektów zamierzonych posunięć gospodarczych,
stopnia realizacji przyjętych celów,
odchyleń od wyznaczonych celów.
W literaturze wprowadza się też pojęcie predykcji (predykcji ekonometrycznej) i rozumie się predykcję jako ogół zasad i metod wnioskowania o przyszłości na podstawie rozważanego modelu ekonometrycznego. Prognoza w tym ujęciu to skonkretyzowany proces wnioskowania lub wynik tego wnioskowania.
2. Metody prognozowania
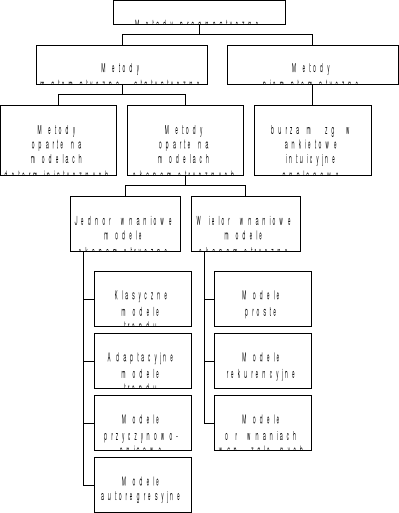
Schemat głównych metod prognostycznych (Zeliaś, 1997, Teoria prognozy)
3. Rodzaje prognoz - klasyfikacja
Kryterium podziału |
Rodzaje prognoz |
Horyzont czasowy |
Długoterminowe - ponad 2 lata Średnioterminowe - do 2 lat Krótkoterminowe - 1 do 3 miesięcy Bezpośrednia - do 1 miesiąca Bieżąca - do kilku dni
Operacyjna - do planowania bieżącej działalności (najczęściej średnioterminowe) Strategiczna - do podejmowania długofalowych decyzji (długoterminowe czasem średnioterminowe)
|
Charakter lub struktura |
Proste - dotyczące jednej zmiennej ekonomicznej - budowane bez udziału innych prognoz, Złożone - dotyczące więcej niż jednej zmiennej ekonomicznej - konstruowane na podstawie innych prognoz
Jakościowe - prognoza nie wyraża się liczbą lecz jakościowo Ilościowe - wielkość prognozy wyraża się liczbą - punktowe, przedziałowe, - skalarne, wektorowe,
Jednorazowe, powtarzalne; Kompleksowe - całościowo opisujące dane przyszłą sytuację złożonego zjawiska. Sekwencyjne - opis dla kilku momentów lub okresów w przyszłości (sekwencji). Samosprawdzające się, destrukcyjne.
|
Stopień szczegółowości |
Ogólne (globalne) - opisujące zjawisko agregat, Szczegółowe - opisujące pewien aspekt badanego zjawiska.
|
Zakres ujęcia |
Całościowe (globalne), częściowe (odcinkowe).
|
Zasięg terenowy |
Światowe, międzynarodowe, krajowe, regionalne.
|
Metoda opracowania |
Minimalne, średnie, maksymalne. Czyste (pierwotne) - ekstrapolacja obserwowanego trendu (krótkoterminowe), często tylko prognozy wstępne. Weryfikowalne - zazwyczaj prognozy powtarzalne, weryfikowane na podstawie napływających danych. Modelowe - zbudowane na podstawie pewnego modelu (ekonometrycznego).
Predykcje ilościowe Prognozy nieobciążone - nie niosące systematycznego błędu, założenie co do wartości oczekiwanej prognozy. Prognozy budowane metodą największego prawdopodobieństwa - związane z metodą estymacji współczynników modelu, wybieramy wielkości „najbardziej” prawdopodobne. Minimalizujące oczekiwaną stratę - metoda niosąca wartościowanie ekonomiczne, funkcję straty. Prognoza uwzględnia prawdopodobieństwo wystąpienia zjawiska i stratę związaną z jego wystąpieniem.
Predykcje jakościowe Predykcja punktów zwrotnych - przewidywanie wystąpienia momentów zmiany tendencji (np. ze wzrostowej na spadkową). Predykcja przewyższeń - budowanie prognozy mówiącej, że w pewnym okresie zmienna prognozowana osiągnie wartości wyższe (lub niższe) od z góry ustalonych. Zazwyczaj tą wartością jest jakiś poziom istotny z ekonomicznego punktu widzenia. Predykcja ciągów monotonicznych - prognoza czy utrzyma się tendencja spadkowa lub wzrostowa.
|
Cel lub funkcja |
Prognozy badawcze - mają na celu zrozumienie i poznanie zjawiska. ostrzegawcze - mające na celu zwrócenie uwagi na niekorzystne zjawiska, normatywne - mające ustalić pewne obowiązujące normy, powinny być zrealizowane aktywne - pobudzające do działania, pasywne - zniechęcające do działania.
Wspomagająca ( przygotowująca, preparacyjna) - wspomagająca działalność, podejmowanie decyzji. Aktywizująca Informacyjna
|
(Zeliaś, 1997, Teoria prognozy)
Przykład 1
W marcu 2004 wykonano prognozę dotyczącą sytuacji finansowej Firmy w maju 2004. Prognozowano wielkość produkcji, stan zapasów, wielkość sprzedaży, ściągalność należności, przepływy finansowe uwzględniające zmiany kursów walut.
Określić wykonaną prognozę na podstawie podanych na wykładzie kryteriów (klasyfikacji).
Rozwiązanie
Jest to prognoza:
krótkoterminowa - 2 miesiące,
operacyjna - związana z bieżącą działalnością,
złożona - sytuacja finansowa opisana przez więcej niż jedną zmienną,
ilościowa - prognoza wyraża się wielkościami mierzalnymi, prognozy finansowe zazwyczaj są ilościowe,
może być zarówno punktowa jak i przedziałowa,
wektorowa - wynikiem prognozy jest komplet liczb, a więc może być traktowany jak wektor,
jednorazowa - obliczona tylko raz w marcu 2004, nic nam nie wiadomo, żeby miała być robiona powtarzalnie,
kompleksowa - dotyczy całości sytuacji Firmy,
nie wiemy czy jest samospełniająca czy destrukcyjna,
ogólna - dotyczy całej Firmy, a nie jakiegoś aspektu działania Firmy, byłaby szczegółowa gdyby dotyczyła jednej firmy będącej częścią większego zespołu firm,
całościowa - dotyczy całej Firmy, byłaby częściowa gdyby dotyczyła jednej firmy z dużego zespołu firm,
regionalna - Firma związana jest z regionem,
nie wiemy jako była metoda opracowania
ze względu na cel lub funkcję - jest badawcza, celem jest rozpoznanie prawdopodobnej sytuacji finansowej Firmy,
ze względu na cel lub funkcję - może być ostrzegawcza, aktywna, pasywna.
4. Horyzont prognozy
Oznaczenia: Yt - zmienna opisująca badane zjawisko ekonomiczne,
t - zmienna czasowa
(t - oznacza moment lub okres, t = 1, 2, 3, …m),
yt - szereg czasowy realizacji zmiennej Yt w badanych momentach lub okresach,
Id - przedział czasowy w którym są zbierane dane statystyczne,
td - środek przedziału Id.
Horyzont prognozy to przedział postaci:
(tb , T]
gdzie: tb okres (chwila) bieżąca, T okres (chwila) końcowa
Wyprzedzenie czasowe prognozy h' (w stosunku do bieżącego okresu), to długość horyzontu prognozy, czyli:
h' = T - tb
Horyzont predykcji (dla bieżącego okresu) to przedział postaci:
(tb , tb + 2]
gdzie: tb okres (chwila) bieżąca, 2 długość horyzontu predykcji wynikająca z przyjętego modelu prognostycznego. 2 jest trudne to określenia, zazwyczaj pełni funkcję teoretyczną.
Niech 1 oznacza czas niezbędny do podjęcia efektywnych kroków mogących wpłynąć na prognozowane zjawisko.
Jeśli zachodzą nierówności:
1 ≤ h' ≤ 2
to możliwa jest reakcja na wyniki prognozy.
Opóźnienie bieżące modelu 0 (w stosunku do bieżącego okresu) to odległość między okresem bieżącym i środkiem przedziału zbierania danych:
0 = tb - td
Predyktywne opóźnienie modelu L to suma opóźnienia bieżącego modelu i wyprzedzenia czasowego prognozy
L = 0 + h' = T - td
Wyjściowy okres prognozy tn - to ostatni okres dla którego dysponujemy informacją o rzeczywistej wartości zmiennej prognozowanej.
Horyzont predykcji (dla wyjściowego okresu prognozy) to przedział: (tn , tn + 2)
Opóźnienie w dopływie danych statystycznych 3 = tb - tn .
Realne wyprzedzenie czasowe prognozy h to długość okresu na który się prognozuje (od wyjściowego okresu prognozy):
h = T - tn = h' + 3 = T - tb + 3 .
Zachodzą więc nierówności:
h' ≤ h ≤ 2 .
Przykład 2
Od stycznia 2000 roku do grudnia 2003 obserwowano miesięczne wielkość zmiennej Yt. W lutym 2004 wykonano prognozę dla maja 2004.
Oblicz wielkości związane z horyzontem prognozy:
zakres zmienności zmiennej czasowej t;
Id przedział w którym zbierane są dane;
td środek przedziału w którym zbierane są dane;
tb bieżący okres;
tn wyjściowy okres prognozy;
T okres końcowy;
(tb , T] horyzont prognozy;
h' wyprzedzenie czasowe prognozy (w stosunku do bieżącego okresu);
0 opóźnienie bieżące modelu (w stosunku do bieżącego okresu);
L predyktywne opóźnienie modelu;
3 opóźnienie w dopływie danych statystycznych;
h realne wyprzedzenie czasowe prognozy;
Rozwiązanie
t przybiera wartości od 1 do 53; ilość miesięcy od stycznia 2000 do maja 2004;
[1, 48] począwszy od stycznia 2000 do grudnia 2003 włącznie;
td = 24,5 środek przedziału [1, 48];
tb = 50 numer miesiąca „luty 2004” przy numeracji zaczynającej się od miesiąca „styczeń 2000”;
tn = 48 numer miesiąca „grudzień 2003” ;
T = 53 numer miesiąca „maj 2004”;
(50 , 53] ;
h' = T - tb = 53 - 50 = 3;
0 = tb - td = 50 - 24,5 = 25,5;
L = T - td = 53 - 24,5 = 28,5;
3 = tb - tn = 50 - 48 = 2;
h = T - tn = 53 - 48 = 5;
Przykład 3
Od 1 lipca 2000 roku do 15 grudnia 2001 obserwowano codziennie wielkość zmiennej Yt. W dniu 28 grudnia 2001 zbudowano prognozę dla 10stycznia 2002.
Oblicz wielkości związane z horyzontem prognozy:
zakres zmienności zmiennej czasowej t;
Id przedział w którym zbierane są dane;
td środek przedziału w którym zbierane są dane;
tb bieżący okres;
tn wyjściowy okres prognozy;
T okres końcowy;
(tb , T] horyzont prognozy;
h' wyprzedzenie czasowe prognozy (w stosunku do bieżącego okresu);
0 opóźnienie bieżące modelu (w stosunku do bieżącego okresu);
L predyktywne opóźnienie modelu;
3 opóźnienie w dopływie danych statystycznych;
h realne wyprzedzenie czasowe prognozy;
5. Błąd prognozy ex post i ocena ex ante błędu
Dwa podstawowe postulaty predykcji to:
Prognoza powinna być obliczona wraz z odpowiednim miernikiem rzędu dokładności.
Przy wyborze sposobu budowania prognozy należy dążyć do wysokiej efektywności predykcji, czyli osiągnięcia zadowalającego rzędu dokładności predykcji.
Wyróżniamy dwa rodzaje mierników dokładności predykcji:
Mierniki dokładności ex ante - ocena błędu ex ante, ocena spodziewanej wartości rzeczywistych wartości zmiennej prognozowanej od prognozy.
Mierniki dokładności ex post - wielkość błędu ex post, wartość odchylenia prognozy od rzeczywistej zrealizowanej wartości zmiennej.
6. Prognozy dopuszczalne
Wiele jest kryteriów dopuszczalności prognoz. Dopuszczalność prognozy jest ważnym zagadnieniem.
Prognoza jest dopuszczalna jeśli realne wyprzedzenie czasowe jest nie większe niż długość horyzontu predykcji: h ≤ 2.
Horyzont prognozy zależy od wybranego modelu prognostycznego, zależy też inercji zmiennych objaśnianych.
Zwiększenie pewności prognozy można osiągnąć stosując kilka metod prognozowania.
7. Dane statystyczne wykorzystywane w prognozowaniu.
Ważny etap prac prognostycznych to pozyskanie danych statystycznych. Na ich podstawie następuje wybór klasy modelu prognostycznego (predykcji) czyli postaci zależności, oszacowań parametrów, weryfikacji prognoz wygasłych itd.
Liczbowe dane statystyczne powinny być:
jednorodne
rzetelne
jednoznaczne
porównywalne w czasie i przestrzeni
kompletne
aktualne dla przyszłości.
Wyróżnia się dwa rodzaje błędów:
błędy systematyczne (nielosowe)
błędy przypadkowe (losowe).
Podstawowe źródła błędów w trakcie zbierania i opracowywania danych to:
niedokładność
trudności z określeniem (zmierzeniem) badanej wielkości
opuszczenie lub wielokrotne ujęcie tych samych wielkości
niejasne lub zbyt ogólne pytania w formularzu pytań lub zła interpretacja odpowiedzi
świadome lub nieświadome udzielanie fałszywych informacji
niedokładność pomiarów lub obliczeń
błędy w czasie przepisywanie (przepływie danych)
błędy klasyfikacji, segregacji, tabulacji.
Błędy systematyczne są groźne. Błędy losowe nie są bardzo groźne.
8. Szacowanie brakujących danych (ilościowych i jakościowych)
Braki danych ilościowych związane są z niedostępnością danych statystycznych.
Braki danych związane z niedostępnością danych jakościowych.
Przy braku danych niemożliwe jest bezpośrednie wykorzystanie klasycznych metod ekonometrycznych.
Stosujemy jedną z trzech metod:
ograniczamy przekroje analizy, tzn. eliminujemy te zmienne dla których brakuje danych,
wykorzystujemy niekompletne dane i stosujemy nie ekonometryczne metody prognozy: burzę mózgów, szacunki ekspertów, metody analogowe itp.
na podstawie dostępnych danych źródłowych szacujemy brakujące dane.
9. Prognozy w procesie decyzyjnym
Jaką rolę powinna odgrywać prognoza w procesie decyzyjnym?
Decyzja zazwyczaj podejmowana jest w warunkach niepewności. Prognoza oparta na posiadanej wiedzy i naukowych metodach matematyki i statystyki, pozwala redukować niepewność przyszłości.
Redukcja niepewności zależy od wielu czynników. Niektóre prognozy są nieomal bezbłędne, inne obciążone dużą dozą niepewności. Prognozy ekonometryczne zazwyczaj są obciążone dużą niepewnością.
Potrzebne są dodatkowe kryteria lub metody przy podejmowaniu decyzji w warunkach niepewności.
„Naiwna strategia postępowania” postępujemy tak, jakby prognoza była pewna.
Maksymalizowanie korzyść - jeśli potrafimy powiązać wielkość korzyści z prognozowanymi stanami wielkości Yt oraz potrafimy oszacować prawdopodobieństwa trafności danego wariantu prognozy, to możemy tak postępować by maksymalizować wartość oczekiwaną korzyści.
Możemy też tak postępować by maksymalizować osiągany zysk (korzyść).
Można zwiększać trafność prognozy przez zwiększanie nakładów na prognozę. Nie zawsze jednak jest to opłacalne.
Jakość prognozę oceniamy oceniając jej trafność. Trafność prognozy oceniamy za pomocą określania błędów ex post. Jest to jednak możliwe tylko dla prognoz ilościowych.
Wykład 2
Zasady budowania prognoz ekonometrycznych
1. Wybór modelu prognostycznego.
Pierwszy etap. Określenie zjawisko, które chce się prognozować. Wybór postaci analitycznej funkcji prognozy. Wybór modelu ekonometrycznego (modelu prognostycznego). Wybór postaci zależności w ramach wybranego modelu prognostycznego.
Możemy oprzeć się na zebranym materiale statystycznym i na jego analizie:
Analiza graficzna,
Analiza ilościowa - analiza dopasowania modelu do danych statystycznych.
Możemy oprzeć się na teorii ekonomicznej:
Korzystanie ze znanych i sprawdzonych zależności występujących między wielkościami ekonomicznymi
Możemy oprzeć się na doświadczeniu zebranym przy budowaniu podobnego typu prognoz oraz na towarzyszącym prognozowaniu badaniach.
Przyjęcie danego modelu prognostycznego związane jest z:
możliwością jasnej interpretacji ekonomicznej parametrów modelu,
możliwością względnie łatwej estymacji parametrów modelu,
stopniem dokładności, z jakim model opisuje badane zjawisko (w przeszłości i przyszłości).
Należy też dobrać zmienne objaśniające. Istnieje wiele metod doboru zmiennych objaśniających. Np:
odwołanie się do istniejącej teorii,
analiza materiału empirycznego,
wybranie zmiennych najsilniej skorelowanych ze zmiennymi objaśnianymi.
Drugi etap. Zebranie danych statystycznych, na podstawie których będą oszacowane parametry występujące w modelu. Dane powinny być: rzetelne, zgodne z przedmiotem badań, jednoznaczne, kompletne, aktualne, porównywalne w czasie i przestrzeni. Powinny być wyeliminowane dane odstające, rzadkie, obce. Możliwa jest redukcja danych objaśniających na tym etapie.
Trzeci etap. Estymacja parametrów modelu. Często metodą najmniejszych kwadratów.
Czwarty etap. Weryfikacja modelu. Czy otrzymane parametry strukturalne modelu są zgodne z obserwowaną rzeczywistością.
Piąty etap. Praktyczne wykorzystanie zbudowanego modelu. Do opisu rzeczywistości, wnioskowania o przyszłości, podejmowania decyzji.
2. Podstawowe założenia występujące przy wnioskowaniu o przyszłości.
Klasyczne założenia teorii predykcji:
znajomość modelu kształtowania się zmiennej prognozowanej,
znajomość postaci analitycznej
znajomość parametrów strukturalnych, stochastycznych
stabilność w czasie prawidłowości ekonomicznej na której opiera się model,
stabilność w czasie zarówno w przedziale z którego pochodzą dane do estymacji jak i w okresie prognozy,
stabilność rozkładu czynnika losowego (zaburzenia, błędu),
stabilność co najmniej do okresu T,
znajomość wartości zmiennych objaśniających model w okresie na który budowana jest prognoza,
znajomość dla okresu T zmiennych objaśniających jest istotnym ograniczeniem do stosowania modeli przyczynowo-skutkowych i wielorównaniowych modeli ekonometrycznych, ograniczeniem do przypadku, gdy zmienne objaśniające są zmiennymi planowanymi niezależnymi od innych czynników,
dopuszczalność ekstrapolacji modelu poza obserwowany w „próbie” obszar zmienności zmiennych objaśnianych.
najbardziej kłopotliwe założenie, służy ograniczeniu bezkrytycznych uogólnień.
Przyjmujemy, że klasyczne założenia teorii predykcji przy krótkookresowych prognozach są zawsze spełnione. Przy prognozach długookresowych klasyczne założenia teorii predykcji są zbyt restrykcyjne.
Zmodyfikowane założenia teorii predykcji:
znajomość modelu kształtowania się zmiennej prognozowalnej uwzględniająca możliwe małe niestabilności tej prawidłowości,
stabilność lub zachowanie się „bliskie” stabilności w czasie badanego zjawiska,
stabilność lub zachowanie się „bliskie” stabilności w czasie składnika losowego,
znajomość wartości zmiennych objaśniających model lub rozkładu tych zmiennych, w okresie na który wykonywana jest prognoza,
możliwość ekstrapolacji modelu poza obszar zmienności zaobserwowanej w „próbie” z błędem nie większym niż zadany z góry.
3. Zasady budowy predykcji ilościowych
Predykcja punktowa.
zasada nieobciążoności predykcji (zasada statystyczna)
yPT = E(YT)
zasada największego prawdopodobieństwa predykcji (zasada statystyczna)
yPT = M(YT)
zasada minimalizacji funkcji straty (zasada ekonomiczna)
E[W(YT - yPT)] = min { E[W(YT - y^PT)] ; y^PT dowolna predykcja}
Predykcja przedziałowa
Ustalamy z góry wiarygodność predykcji γT , należy wskazać przedział IPT spełniający:
P( YT ∈ IPT ) = γT
Wiarygodność predykcji γT to liczba z przedziału [0, 1], zazwyczaj γT ≥ 0,9.
4. Miary dokładności wnioskowania w przyszłość EX ANTE
W predykcji punktowej możemy rozważać następujące błędy:
DT = YT - yTP - błąd predykcji, zmienna losowa
D'T = YT - YTP - pełny błąd predykcji, YTP zmienna losowa, brak oszacowań parametrów modelu
D*T = YT - ES(YTP) - czysty błąd predykcji, ES(.) to wartość oczekiwana po wszystkich możliwych zbiorach danych, zgodnie z ich rozkładem.
W praktycznych obliczeniach stosuje się najczęściej błąd predykcji. Oszacowanie parametrów rozkładu błędu predykcji ex ante jest często stosowanym miernikiem jakości wnioskowania w przyszłość. Szacujemy parametry:
E(DT) - obciążenie predykcji,
var(DT) - wariancja predykcji,
σ(DT) = (var(DT))0,5 - odchylenie standardowe predykcji (średni błąd predykcji),
V(DT) = σ(DT) / |yTP| - względny błąd predykcji.
W predykcji przedziałowej stosujemy często następujące mierniki dokładności predykcji ex ante:
wiarygodność predykcji γT (z góry ustalona) ,
precyzja predykcji d(IPT) - połowa przedziału predykcji IPT ,
względna precyzja predykcji V(IPT) = d(IPT) / | yPT|
5. Miary dokładności wnioskowania w przyszłość EX POST
Ocenę ex post możemy przedstawić jako ocenę dla prognoz wygasłych.
Prognoza wygasła to prognoza dla okresu t, dla którego znana jest już prawdziwa wartość zmiennej prognozowanej Yt , czyli t ∈ Id (zamiast T piszemy teraz t).
Oznaczmy:
Iemp - okres weryfikacji empirycznej prognozy,
m - ilość okresów w Iemp , czyli ilość okresów w których następuje empiryczna weryfikacja.
Mierniki dokładności predykcji ex post:
Średnie obciążenie predykcji ex post:
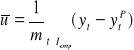
Względne obciążenie predykcji ex post:
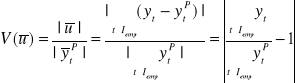
Średni błąd predykcji ex post:
![]()
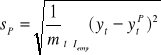
Względny błąd predykcji ex post:
![]()
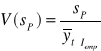
Współczynnik Theila
![]()
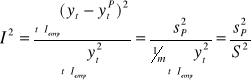
gdzie ![]()
Całkowity względny błąd predykcji
![]()
![]()
Rozkład współczynnika Theila na sumę trzech składników pozwala ocenić źródła błędów predykcji
I2 = I12 + I22 + I32
gdzie:
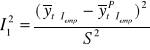
określa obciążenie predykcji
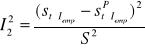
określa niedostateczność elastyczności predykcji
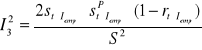
określa niedostateczność predykcji punktów zwrotnych
gdzie:
![]()
- średnie arytmetyczne, odpowiednio, wartości rzeczywistych i wygasłych prognoz;
![]()
- odchylenia standardowe, odpowiednio, wartości yt i ytP;
![]()
- współczynnik korelacji liniowej między wartościami yt i ytP;
dla t ∈ Iemp czyli na przedziale empirycznej weryfikacji prognoz.
Dzieląc rozkład z punktu 7. przez współczynnik Thiela I2 dostajemy:
![]()
gdzie interpretujemy:
![]()
jako miernik całkowitego względnego obciążenia predykcji wynikającego z obciążenia predykcji (małej zgodności średnich wartości yt i ytP w przedziale Iemp),
![]()
jako miernik całkowitego względnego obciążenia predykcji wynikającego z niedostatecznej elastyczności predykcji (małej zgodności zróżnicowania wartości yt i ytP w przedziale Iemp),
![]()
jako miernik całkowitego względnego obciążenia predykcji wynikającego z niedostatecznej predykcji punktów zwrotnych (małej zgodności kierunków zmian wartości yt i ytP w przedziale Iemp),
Do badania dopuszczalności prognoz stosowany jest również współczynnik Janusowy:
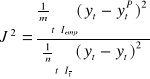
w liczniku występuje wariancja średniego błędu predykcji ex post, w mianowniku wariancja resztowa modelu.
Współczynnik Janusowy pozwala badać aktualność modelu. Na jego podstawie oceniamy, czy model nadal jest aktualny.
Jeżeli J2 ≤ 1 + δ dla δ małej liczby rzeczywistej (nieco większej od zera) to model nadal jest aktualny. Wariancja średniego błędu predykcji ex post nie jest dużo większa od wariancji resztowej modelu. Jeżeli J2 jest dużo większe od 1 uznajemy, że model już się zdezaktualizował.
Mierniki dokładności predykcji (zarówno ex ante jak i ex post) dzielimy na mierniki bezwzględne (zachowujące „jednostkę” miary) i względne (procentowe).
Jeżeli odbiorca prognozy nie ma własnych kryteriów dopuszczalności prognozy, to przyjmujemy następującą ocenę dokładności (zarówno ex post jak i ex ante):
V ≤ 3% - prognoza bardzo dobra,
3% < V ≤ 5% - prognoza dobra,
5% < V ≤ 10% - prognoza może być dopuszczalna,
10% < V - prognoza nie jest dopuszczalna,
Przykład 1 (Zeliaś, przykład 2.2 str. 53)
Prognozowana jest wartość indeksu WIG (na zamknięciu sesji) na GPW w Warszawie. Szereg czasowy obserwacji („próby”) składa się z 10 momentów zamknięcia sesji od 27 listopada 2000 do 8 grudnia 2000.
Obliczono prognozę sekwencyjną dla T = 11, 12, 13 (11, 12, 13 grudnia 2000).
Dane i obliczenia w tabeli 1.
Średnia rzeczywistych wartości WIG w okresach 11, 12, 13 wynosi: yśrT = 17.089,05
Średnia wartości prognoz WIG w okresach 11, 12, 13 wynosi: yPśrT = 17.056,75
Średnia prognozy ma niższą wartość od średniej wartości rzeczywistych, może to wskazywać na to, że prognozy są obciążone.
Różnica średnich czyli średnie obciążenie ex post prognozy: ![]()
= uśr = yśrT - yPśrT = 32,30
A więc istotnie prognoza jest obciążona, niedoszacowanie wynosi 32,2 punktu.
Czy występujące obciążenie prognozy jest dużym obciążeniem? Liczymy względne obciążenie ex post prognozy:
V(uśr) = | uśr | / | yśrT | = 32,30 / 17.056,75 = 0,19%
Obciążenie prognozy jest bardzo małe.
Średni błąd prognozy ex post wynosi:
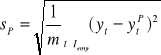
= 37,33
Względny błąd prognozy ex post wynosi:
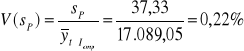
Średni błąd prognozy to 37,33 jest to jednak zaledwie 0,22% średniej wartości rzeczywistej.
Współczynnik Theila:
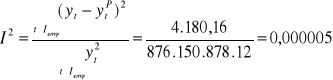
Względny błąd predykcji ex post wynosi:
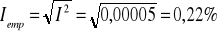
Identyfikując przyczyny błędu korzystamy z rozkładu współczynnika Thiela I2 = I12 + I22 + I32 :
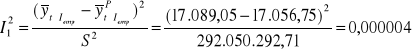
obciążenie predykcji
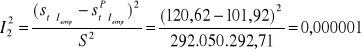
niedostateczność elastyczności predykcji
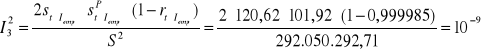
niedostateczność predykcji punktów zwrotnych
Wyliczymy teraz udział procentowy tych błędów w całkowitym błędzie ex post:
![]()
![]()
![]()
![]()
Obliczmy współczynnik Janusowy:
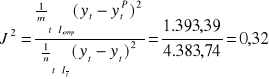
ponieważ współczynnik jest mniejszy od 1 model nadal jest aktualny.
Wykład 3
Prognozowanie na podstawie klasycznych modeli trendu
Interesuje nas dyskretny proces stochastyczny (Yt)t=1,2,….Zaobserwowane wartości tego szeregu oznaczamy: y1, y2,… yn i nazywamy szeregiem czasowym. Możemy rozważać szereg czasowy momentów lub okresów. Dodatkowo zakładamy, że odstępy czasowe są równe.
Zdajemy sobie sprawę z tego, że zaobserwowane wartości Y nie musiały wystąpić, mogły być inne bliskie bądź dalekie od zanotowanych. Obserwowany proces jest procesem stochastycznym. Przyjmujemy następujący model opisu obserwowanego procesu. Przyjmujemy, że jest on wypadkową działania:
składowej deterministycznej (składowa systematyczna, przyczyny główne);
trendu
stałego poziomu;
składowej okresowej:
wahań cyklicznych;
wahań sezonowych;
procesu stochastycznego (przyczyn ubocznych, przypadkowych).
Proces wyznaczania składowych szeregu czasowego nazywamy procesem dekompozycji szeregu czasowego. Proces dekompozycji polega na budowie modelu szeregu czasowego.
Wyróżniamy dwa główne typy modelu szeregu czasowego:
addytywny: yt = f(t) + g(t) + h(t) + ξt ; t = 1, 2, … n ;
multiplikatywny: yt = f(t) ⋅ g(t) ⋅ h(t) ⋅ ξt ; t = 1, 2, … n ;
gdzie:
f() - funkcja opisująca trend ;
g() - funkcja opisująca wahania sezonowe ;
h() - funkcja opisująca wahania cykliczne ;
ξt - składnik losowy.
Budując model musimy ustalić postać analityczną funkcji f, g, h. Krokiem w kierunku ustalenia postaci funkcji może być analiza graficzna zaobserwowanych wielkości y1, y2¸ … yn i na tej podstawie próba ustalenia postaci funkcji trendu.
Przyjmiemy, że funkcja trendu jest funkcją:
liniową, gdy (t, yt) układają się w przybliżeniu wzdłuż linii prostej; (yt = a + bt)
wykładniczą, gdy (t, ln(yt)) układają się w przybliżeniu wzdłuż linii prostej; (yt = a ⋅ bt)
logarytmiczną, gdy (ln(t), yt) układają się w przybliżeniu wzdłuż linii prostej; (yt = a ⋅ ln(t))
potęgową, gdy (ln(t), ln(yt)) układają się w przybliżeniu wzdłuż linii prostej; (yt = a ⋅ tb)
Musimy teraz zweryfikować wybór analitycznej postaci funkcji trendu.
Ad a) Jeśli funkcja trendu ma postać liniową f(t) = a + b⋅t , to przyrosty są stałe (z dokładnością do składnika losowego):
Δyt = yt - yt-1 = b + (ξt - ξt-1) ;
Weryfikujemy hipotezę, o stałości przyrostów zakładając liniowość przyrostów: Δyt = α + β⋅t + εt ;
a następnie weryfikując hipotezę zerową H0 , że parametr β różni się od zera w sposób nieistotny.
Ad b) Jeśli funkcja trendu ma postać wykładniczą f(t) = a ⋅ bt , to spełniony jest warunek:
( f(t) - f(t-1) ) / f(t-1) = b - 1
A to oznacza, że szereg czasowy ma stałe przyrosty względne (z dokładnością do składnika losowego) lub inaczej mówiąc, że indeksy łańcuchowe dla tego szeregu są stałe z dokładnością do czynnika losowego:
Δyt / yt - yt-1 = const + εt ;
Prognozowanie na podstawie trendu.
Rozważmy obecnie modele szeregów czasowych, w których składowa systematyczna ma postać trendu oraz w których występuje składowa losowa. Rozważamy więc modele postaci:
Yt = f(t) + ξt - postać addytywna (A)
Yt = f(t) ⋅ ξt - postać multyplikatywna (M)
dla t = 1, 2, …n
Będziemy obecnie zakładać, że f jest funkcją liniową: f(t) = α0 + α1⋅t
Dodatkowo zakładamy, że :
w modelu (A) addytywnym E(ξt) = 0 ;
w modelu (M) multyplikatywnym E(ξt) = 1 ;
Tak więc model szeregu czasowego ma postać:
yt = α0 + α1⋅t + ξt , t = 1, 2, … n;
Parametry α0 , α1 są nam nieznane. Musimy je oszacować. Szacujemy za pomocą metody najmniejszych kwadratów i jako wynik dostajemy a 0 , a1 :
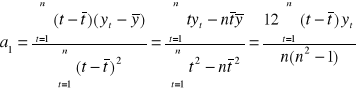
![]()
gdzie ![]()
są średnimi arytmetycznymi
Szereg czasowy możemy więc przedstawić następująco:
yt = a0 + a1⋅t + et ; t = 1, 2, … n ;
gdzie
![]()
to reszty modelu;
zaś ![]()
to wartości teoretyczne prognozowanej zmiennej
Model trendu możemy zapisać w postaci macierzowej: y = X α + ξ
gdzie:
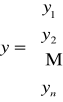
, 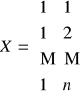
, 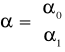
, 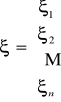
.
Przez a oznaczmy oszacowanie wektora α za pomocą metodą najmniejszych kwadratów. Wektor a dany jest więc wzorem:
![]()
![]()
Zachodzi tożsamość:
y = X a + e
gdzie e to wektor reszt: e = y - X a = ![]()
zaś ![]()
to wektor wartości teoretycznych prognozowanej zmiennej.
Weryfikacja modelu trendu liniowego - ocena dopasowania do danych empirycznych.
Wariancja resztowa:
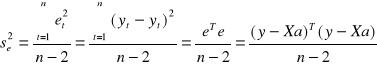
Standardowe odchylenie składnika resztowego:
![]()
Współczynnik zmienności resztowej
![]()
Zakładamy z góry pewną wartość krytyczną V* współczynnika zmienności losowej, np. V*=10%. Jeśli zachodzi nierówność:
Ve ≤ V*
to model uważamy za dostatecznie dopasowany do zmiennych empirycznych.
Współczynnik zbieżności ϕ2 :
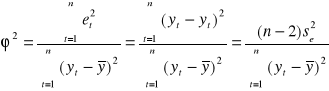
Współczynnik zbieżności przyjmuje wartości z przedziału [0, 1], informuje on jaka część całkowitej zmienności zmiennej objaśnianej nie jest wyjaśniona przez model. Dopasowanie modelu do danych jest tym lepsze im mniejsze jest ϕ2.
Współczynnik determinacji R2 :
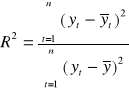
Współczynnik determinacji przyjmuje wartości z przedziału [0, 1], informuje on jaka część całkowitej zmienności zmiennej objaśnianej jest wyjaśniona przez model. Dopasowanie modelu do danych jest tym lepsze im większe jest R2.
Zachodzi równość: ϕ2 + R2 = 1 .
Współczynnik korelacji wielorakiej R:
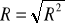
Dopasowanie modelu do danych empirycznych weryfikuje się poprzez weryfikację hipotezy o istotności współczynnika determinacji (korelacji wielorakiej). Testuje się hipotezę zerową postaci H0 : [R2 = 0] przeciwko hipotezie alternatywnej H1 : [R2 ≠ 0].
Hipotezę testujemy przy pomocy statystyki F Fishera-Snedecora o m1 = k i m2 = (n - k - 1) stopniach swobody, gdzie k to ilość zmiennych objaśniających (u nas obecnie k = 1), n to ilość obserwacji. U nas m1 = 1; m2 = n - 2. Hipotezę testujemy na zadanym poziomie istotności γ (np. γ = 0,05).
![]()
Jeśli wykonujemy obliczenia „ręcznie” to dla ustalonego poziomu istotności γ wyznaczamy z tablic wartość krytyczną F* dla m1 , m2 stopni swobody.
Jeśli mamy do dyspozycji arkusz kalkulacyjny Excel to możemy wyznaczyć wartość krytyczną F* przy pomocy funkcji
=ROZKŁAD.F.ODW(γ; m1; m2)
Jeśli F ≤ F* to nie ma podstaw do odrzucenia hipotezy H0 , czyli przyjmujemy, że współczynnik determinacji jest nieistotnie różny od zera. Jeśli F > F* to odrzucamy hipotezę H0 na rzecz hipotezy alternatywnej H1 , współczynnik determinacji jest istotnie różny od zera.
Jeśli mamy do dyspozycji arkusz kalkulacyjny Excel oraz dysponujemy danymi, możemy wykonać wszystkie obliczenia w Excelu.
Weryfikacja modelu polega na weryfikacji hipotez o istotności po kolei każdego parametru. Stawiamy więc hipotezę zerową H0 : [αi = 0] wobec hipotezy alternatywnej H1 : [αi ≠ 0] . Hipotezy weryfikujemy statystyką t-Studenta dla n-2 stopni swobody:
![]()
, i= 0, 1 .
gdzie:
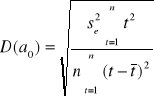
, 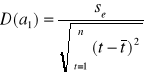
.
Z tablic t-Studenta dla n-2 stopni swobody (n-k-1 stopni swobody) i danego poziomu istotności γ odczytujemy wartość krytyczną![]()
. Jeżeli:
![]()
to odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej. Czyli przyjmujemy, że i-ty parametr jest istotny.
Jeśli mamy do dyspozycji arkusz kalkulacyjny Excel to możemy wyznaczyć wartość krytyczną ![]()
przy pomocy funkcji
=ROZKŁAD.T.ODW(γ; ilość stopni swobody)
W przeciwnym wypadku nie mamy podstaw do odrzucenia H0 , czyli parametr strukturalny αi różni się nieistotnie od zera, a to oznacza, że czas czyli zmienna t nie wpływa w sposób istotny na wartość zmiennej objaśnianej Y.
Prognoza punktowa
Wartość prognozy na okres T = n+1, n+2, … obliczamy zgodnie z zasadą predykcji nieobciążonej przez ekstrapolację oszacowanej funkcji trendu:
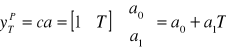
gdzie c traktujemy jak „kolejny” wiersz macierzy obserwacji X, zaś a to wektor oceny parametrów strukturalnych modelu.
Ocena ex ante średniego błędu predykcji wyliczana jest ze wzoru:
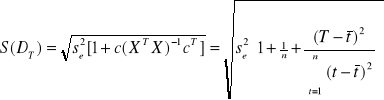
Ocena ex ante względnego błędu predykcji wyliczana jest ze wzoru:
![]()
Prognoza przedziałowa
Przedział predykcji na okres (moment) T budujemy tak, aby:
![]()
gdzie yTP - prognoza punktowa, S(DT) - średni błąd predykcji, γT - wiarygodność predykcji (=0,05 np.), u współczynnik odczytany z tablic dwustronnych t-Studenta dla n-2 stopni swobody i prawdopodobieństwa (1-γT), przy założeniu normalności rozkładu reszt trendu liniowego.
Przykład 1 (Zeliaś 3.1)
Rozpatrujemy zagadnienie predykcji liczby udzielonych noclegów (w mln) w hotelach w Polsce. Dysponujemy danymi:
Rok |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
Okres |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
noclegi (mln) |
6,11 |
6,50 |
6,77 |
7,15 |
7,52 |
8,05 |
8,53 |
8,89 |
9,28 |
Naszym zadanie jest wyznaczenie prognoz punktowych i przedziałowych liczby udzielonych noclegów w hotelach na lata 1999, 2000, 2001.
Prognozy uznamy za dopuszczalne jeśli będą obarczone błędem nie większym niż 4%, zaś wiarygodność prognoz przedziałowych powinna wynosić 95%.
Rozwiązanie
Badamy graficzne przedstawienie danych:
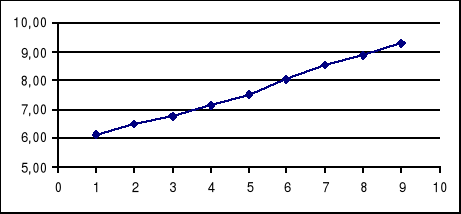
Stwierdzamy, że szereg czasowy ma dwie składowe: trend i wahania losowe. Przyjmujemy, że naszym modelem tendencji rozwojowej będzie liniowa funkcja trendu. Czyli naszym modelem prognostycznym jest :
yt = α0 + α1⋅t + ξt , t = 1, 2, … n;
Przeprowadzimy teraz weryfikację naszego modelu.
Estymacja parametrów
|
t |
yt |
t-tśr |
yt-ytśr |
(t-tśr)2 |
(yt-ytśr)2 |
(t-tśr)(yt-ytśr) |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
6,11 |
-4 |
-1,5344 |
16 |
2,3545 |
6,1378 |
|
2 |
6,50 |
-3 |
-1,1444 |
9 |
1,3098 |
3,4333 |
|
3 |
6,77 |
-2 |
-0,8744 |
4 |
0,7647 |
1,7489 |
|
4 |
7,15 |
-1 |
-0,4944 |
1 |
0,2445 |
0,4944 |
|
5 |
7,52 |
0 |
-0,1244 |
0 |
0,0155 |
0,0000 |
|
6 |
8,05 |
1 |
0,4056 |
1 |
0,1645 |
0,4056 |
|
7 |
8,53 |
2 |
0,8856 |
4 |
0,7842 |
1,7711 |
|
8 |
8,89 |
3 |
1,2456 |
9 |
1,5514 |
3,7367 |
|
9 |
9,28 |
4 |
1,6356 |
16 |
2,6750 |
6,5422 |
Suma |
45 |
68,8 |
0 |
0,0000 |
60 |
9,8640 |
24,2700 |
Średnia |
5 |
7,6444 |
|
|
|
|
|
Obliczamy:
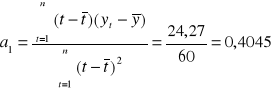
![]()
Oszacowana funkcja trendu ma więc postać:
![]()
Weryfikacja modelu:
Ocenę zgodności danych empirycznych z wartościami teoretycznymi (wynikającymi z postaci modelu) dokonamy na podstawie ocen parametrów struktury stochastycznej, odchylenia standardowego składnika resztowego, współczynnika zmienności resztowej, współczynnika zbieżności i współczynnika determinacji liniowej.
|
t |
yt |
yt^ |
et=yt-yt^ |
(yt-yt^ )2 |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
6,11 |
6,0264 |
0,0836 |
0,0070 |
|
2 |
6,50 |
6,4309 |
0,0691 |
0,0048 |
|
3 |
6,77 |
6,8354 |
-0,0654 |
0,0043 |
|
4 |
7,15 |
7,2399 |
-0,0899 |
0,0081 |
|
5 |
7,52 |
7,6444 |
-0,1244 |
0,0155 |
|
6 |
8,05 |
8,0489 |
0,0011 |
0,0000 |
|
7 |
8,53 |
8,4534 |
0,0766 |
0,0059 |
|
8 |
8,89 |
8,8579 |
0,0321 |
0,0010 |
|
9 |
9,28 |
9,2624 |
0,0176 |
0,0003 |
Suma |
45 |
68,8 |
68,8000 |
0,0000 |
0,0468 |
Średnia |
5 |
7,6444 |
|
|
|
Standardowe odchylenie składnika resztowego:
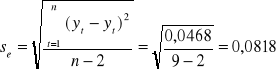
Współczynnik zmienności resztowej
![]()
Współczynnik zbieżności ϕ2 :
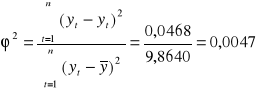
Współczynnik determinacji R2 :
![]()
W arkuszu kalkulacyjnym Excel możemy na wykresie dodać linie trendu i zażądać wyświetlenia równania linii trendu oraz wielkości współczynnika determinacji R2 .
Po zaznaczeniu obiektu wykres wybieramy z menu: Wykres; Dodaj linię trendu; w typie wybieramy liniowy, w opcjach zaznaczamy Wyświetl równanie, Wyświetl R-kwadrat.
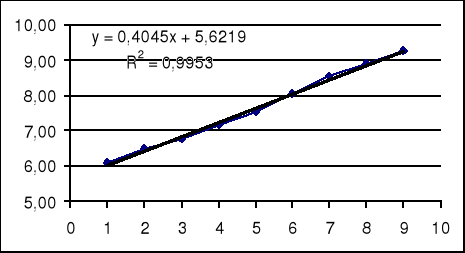
W arkuszu kalkulacyjnym Excel możemy wykonać wszystkie obliczenia wywołując odpowiednie polecenie analizy danych. Jeżeli Analiza danych nie jest dostępna to musimy ją doinstalować z płytki i uaktywnić (Dodatki).
Analizę danych uruchamiamy następująco:
Menu: Narzędzia, Analiza danych, Regresja.
W tabeli regresja zaznaczymy zakres y, zakres x, czy są tytuły, gdzie mają być zapisane wyniki.
PODSUMOWANIE - WYJŚCIE |
|
|
|
Statystyki regresji |
|
Wielokrotność R |
0,997624555 |
R kwadrat |
0,995254753 |
Dopasowany R kwadrat |
0,994576861 |
Błąd standardowy |
0,081772526 |
Obserwacje |
9 |
ANALIZA WARIANCJI |
|
|
|
|
|
|
df |
SS |
MS |
F |
Istotność F |
Regresja |
1 |
9,8172 |
9,817215 |
1468,1603 |
2,14606E-09 |
Resztkowy |
7 |
0,0468 |
0,0066867 |
|
|
Razem |
8 |
9,864 |
|
|
|
|
Współcz. |
Błąd standard. |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Przecięcie |
5,6219444 |
0,059406363 |
94,635392 |
3,876E-12 |
5,481470818 |
5,762418071 |
Zmienna X1 |
0,4045 |
0,010556788 |
38,31658 |
2,146E-09 |
0,379537182 |
0,429462818 |
Prognoza punktowa
Na rok 1999: y10P = 5,6215 + 0,4045 ⋅ 10 = 9,667 mln ,
Na rok 2000: y11P = 5,6215 + 0,4045 ⋅ 11 = 10,071 mln ,
Na rok 2001: y12P = 5,6215 + 0,4045 ⋅ 12 = 10,476 mln ,
Wartości ocen ex ante średnich błędów predykcji obliczonych prognoz:
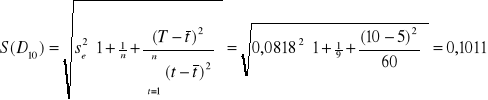
mln
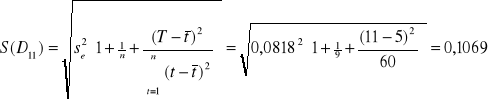
mln
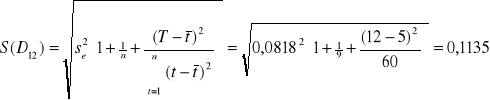
mln
Wartości ocen ex ante względnych błędów predykcji obliczonych prognoz:
![]()
![]()
![]()
Prognoza przedziałowa:
Wartość współczynnika u odczytujemy z tablic dwustronnych rozkładu t-Studenta dla n-2 = 7 stopni swobody i prawdopodobieństwie (1 - 0,95) = 0,05 . Z tablicy odczytujemy, że u = 2,3646 .
Możemy też odczytać z arkusza Excela:
=ROZKŁAD.T.ODW(0,05;7) = 2,36462
Tak więc prognoza przedziałowa na poziomie wiarygodności 0,95 na kolejne lata wynosi:
Na rok 1999: (9,667 - 2,3646 ⋅ 0,1011 ; 9,667 + 2,3646 ⋅ 0,1011) = ( 9,428 ; 9,906 )
Na rok 2000: (10,071 - 2,3646 ⋅ 0,1069 ; 10,071 + 2,3646 ⋅ 0,1069) = ( 9,819 ; 10,324 )
Na rok 2001: (10,476 - 2,3646 ⋅ 0,1135 ; 10,476 + 2,3646 ⋅ 0,1135) = ( 10,208 ; 10,744 )
Wykład 4
Predykcja na podstawie modeli liniowych
Często używanym modelem ekonometrycznym jest jednorównaniony model postaci: Yt = f( Xt1, Xt2, … , Xtk, t)
gdzie Yt - zmienna objaśniana (zależna)
Xt1, Xt2, … , Xtk - zmienne objaśniające (niezależne)
t - składnik losowy
Model ten może być modelem przyczynowo-skutkowym lub opisowym (symptomatycznym).
Zalety modelu:
Przedstawia w prosty sposób (jednym równaniem) zasadnicze związki w analizowanym zjawisku ekonomicznym.
Pozwala łatwo ocenić siłę wpływu poszczególnych zmiennych objaśniających.
Łatwa jest interpretacja parametrów równania.
Umożliwia łatwe budowanie prognoz krótko i średnio terminowych.
Umożliwia łatwą oceny ex ante średnich błędów predykcji.
Umożliwia łatwe uzyskiwania prognoz wariantowych.
Wady modelu:
Dopasowywanie modelu - często musimy modyfikować model, odrzucając jego kolejne wersje.
Dopasowanie postaci analitycznej.
Dobór zmiennych objaśniających.
Eliminowanie współliniowości zmiennych objaśniających.
Badanie stabilności parametrów modelu w czasie.
Konieczność prognozy wartości zmiennych objaśniających na okres na który wyznacza się prognozę zmiennej objaśnianej. Zmienne objaśniające muszą dawać się lepiej prognozować niż zmienna objaśniana.
Skupimy się na jednorównaniowym modelu liniowym lub sprowadzalnym do postaci liniowej. Model taki ma postać wielowymiarowej liniowej funkcji regresji:
Yt = 0·Xt0 + 1·Xt1 + … + k·Xtk + t ; t = 1, 2, …, n ;
gdzie Yt - zmienna objaśniana (zależna)
Xt0, Xt1, … , Xtk - zmienne objaśniające (niezależne) ; X0 = 1;
0, 1,…, k - nieznane parametry modelu
t - składnik losowy
Często wygodnie jest stosować zapis wektorowy: y = X + ;
gdzie:
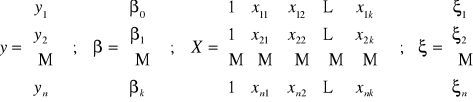
;
y - to wektor zaobserwowanych wartości zmiennej zależnej Yt ;
X - to macierz wartości zmiennych objaśniających
- wektor a priori wartości parametrów równania
- składników losowych równania
Przy klasycznych założeniach modelu regresji liniowej szacujemy parametry 0, 1, … , k metodą najmniejszych kwadratów. Wektor b = [b1, b2, … ,bk] estymata tych parametrów dany jest wzorem:
b = (XT X)-1 XT y
Założenia klasycznej metoda najmniejszych kwadratów:
zmienne objaśniające Xi (i=1, 2,… k) są nielosowe i nieskorelowane z i
rząd(X) = k+1 ≤ n
i ma rozkład N(0,σ2)
zapewniają nam uzyskanie estymatorów o dobrych własnościach: nieobciążonych, zgodnych, efektywnych. Niestety często klasyczne założenia nie są spełnione. Prowadzi do trudności w budowie modelu.
Jedną z trudności jest współliniowość (nadmierne skorelowanie) zmiennych objaśniających.
Wykrywanie i mierzenia stopnia współliniowości zmiennych niezależnych oraz eliminowanie zmiennych współliniowych.
Badamy macierz współczynników korelacji:
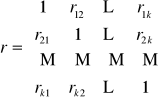
gdzie rij = cor(Xi , Xj ).
Macierz r jest macierzą symetryczną. Wyznacznik tej macierzy det(r) jest miernikiem współliniowości (skorelowania) zmiennych objaśniających. Zachodzi zawsze:
0 ≤ Det(r) ≤ 1 .
Det(r) bliskie 1 świadczy o małym stopniu skorelowania.
Det(r) bliskie 0 świadczy o dużym stopniu skorelowania.
Det(r) jest miarą stabilności modelu. Zwiększanie ilości zmiennych obniża stabilność modelu.
W excelu istnieje funkcja „Wyznacznik.Macierzy()”. Wyznacznik możemy liczyć tylko dla macierzy kwadratowych.
Przypomnienie
a) 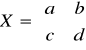
; det(X) = ad - bc ;
b) 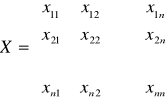
; det(X) = x11⋅det(X11) - x12⋅det(X12) + … + (-1)n+1⋅x1n⋅det(X1n) ;
gdzie Xij to macierz otrzymana z macierzy X przez wykreślenie i-tego wiersza oraz j-tej kolumny.
Przykład
a) 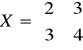
; det(X) = 2 ⋅ 4 - 3 ⋅ 3 = 8 - 9 = -1;
b) 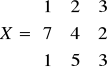
; 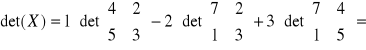
= ![]()
Jeśli det(r) jest zbyt małe, musimy modyfikować model. Możemy eliminować zmienne współliniowe.
Istnienie silnej korelacji między zmiennymi objaśniającymi poważnie wpływa na efektywność estymatorów parametrów modelu. Im większa korelacja tym mniejsza efektywność, tym większa wariancja, tym trudniej poprawnie oszacować parametry strukturalne modelu.
Liczymy test istotności t-Studenta ze statystyką z (n-k-1) stopniami swobody:
![]()
Jeśli t < t*γ,(n-k-1) , to uznajemy oszacowanie parametru za nieistotne. Jeśli t > t*γ,(n-k-1) , to uznajemy parametr za istotny.
Tutaj t*γ,(n-k-1) oznacza wartość krytyczna testu studenta na poziomie istotności γ i z (n-k-1) stopniami swobody, bi to estymata parametru i modelu, zaś D(bi) to ocena średniego błędu parametru i .
Przy wykonywaniu obliczeń przy pomocy „Regresji” z „Analizy danych” Excela dostajemy obliczoną wartość statystyki t dla każdej estymaty parametru (t Stat), a także „Wartość-p”. Wartość p porównujemy z poziomem istotności γ . Jeśli p < γ , to odrzucamy hipotezę o nieistotności parametru i.
Ustalenie zbioru zmiennych objaśniających modelu ekonometrycznego.
Ustalenie wstępnej listy zmiennych objaśniających.
Liczba zmiennych nie może być zbyt duża.
Dobór zmiennych powinien być dokonany na podstawi ich merytorycznej ważności wynikającej z praw ekonomii.
Zmienne powinny mieć wartość merytoryczną i ustalona interpretację.
Zmienne objaśniające powinny być mierzalne.
Zmienne objaśniające powinny mieć silne trendy.
Typując zmienne korzystamy z opinii ekspertów.
Wybieramy zmienne dla których są dostępne kompletne dane statystyczne.
Eliminujemy zmienne quasi-stałe. Badamy współczynnik zmienności Vi porównujemy z wielkością krytyczną V* (np. V* = 0,1). Jeśli Vi < 0,1 to uznajemy zmienną Xi za quasi-stałą i eliminujemy.
Badamy czy zmienna objaśniająca jest istotnie skorelowana ze zmienną objaśnianą (ri - współczynnik korelacji)
Badamy czy zachodzi warunek koincydencji. Czy znak ri współczynnika korelacji jest taki sam jak znak i.
stopień dopasowania modelu do danych empirycznych,
istotność wpływu zmiennych objaśniających na zmienną objaśnianą,
sprawdzenie czy spełnione są założenia dotyczące składnika losowego.
Wariancja resztowa:
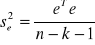
;Standardowe odchylenie składnika resztowego:
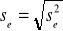
;Współczynnik zmienności resztowej:
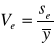
;Współczynnik zbieżności ϕ2 :
Współczynnik determinacji R2 : R2 = 1 - 2
wartość średnia
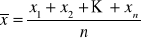
mediana xmed = xn+1 , gdy obserwacje X to x1, x2,… x2n+1; lub
mediana xmed = (xn + xn+1)/2, gdy obserwacje X to x1, x2,… x2n
mediana to wartość leżąca „w środku” między występującymi wartościami X
dominanata xdom - najęściej występująca wartość wśród obserwacji x1, x2,… xn.
wartości skrajne xmin = minimum(x1, x2,… xn) lub xmax = maksimum(x1, x2,… xn)
dolny kwartyl Q1 lub górny kwartyl Q3
Q1 - to „środkowa wartość” (mediana) obserwacji x1, x2,… xn na lewo od mediany xmed
Q3 - to „środkowa wartość” (mediana) obserwacji x1, x2,… xn na prawo od mediany xmed.wartość średnia minus jedno, dwa lub trzy odchylenia standardowe
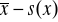
lub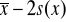
lub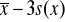
wartość średnia plus jedno, dwa lub trzy odchylenia standardowe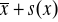
lub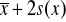
lub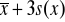
analizę zmienności w czasie badanego zjawiska;
analizę przyczyn zmienności w czasie badanego zjawiska.
przyrosty absolutne o stałej podstawie (jednopodstawowe)
od poziomu zjawiska w danym momencie lub okresie odejmujemy poziom zjawiska z momentu lub okresu przyjętego za podstawę:
(y1-y0), (y2-y0), … (yn-y0)
y0 - poziom zjawiska przyjęty za podstawę
y1, y2,… yn - poziom zjawiska w momentach lub okresach 1, 2, … n.
przyrosty absolutne o podstawie zmiennej (łańcuchowe)
od poziomu zjawiska w danym momencie lub okresie odejmujemy poziom zjawiska z momentu lub okresu bezpośrednio wcześniejszego:
(y2-y1), (y3-y2), … (yn-yn-1)
y1, y2,… yn - poziom zjawiska w momentach lub okresach 1, 2, … n.
przyrosty względne o podstawie stałej (jednopodstawowe):
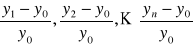
przyrosty względne o podstawie zmiennej (łańcuchowe):
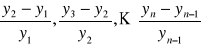
indeksy o podstawie stałej (jednopodstawowe):
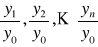
indeksy o podstawie zmiennej (łańcuchowe):
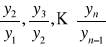
tendencję rozwojową (trend) - powolna systematyczna zmiana poziomu zjawiska, będąca następstwem przyczyn głównych;
wahania sezonowe (okresowe) - powtarzające się regularnie wahania;
wahania przypadkowe (losowe) - odstępstwa od regularnych wahań wywoływane przyczynami ubocznymi lub katastroficznymi.
mechaniczną - polegającą na wygładzaniu szeregu czasowego za pomocą średnich ruchomych
analityczną - polegającą na znalezieniu funkcji (równania) odzwierciedlającej zmienność analizowanego zjawiska; tę funkcję nazywamy funkcją trendu. W najprostszej postaci szukamy funkcji trendu wśród funkcji liniowych.
![]()
Prognozowanie na podstawie jednorównaniowego modelu liniowego y = X + ;
W wyniku estymacji parametrów dostajemy równanie: y = Xb + e ;
Gdzie b to wektor ocen parametrów, wektor e to wektor reszt e = y - b ;
Oszacowany model y = Xb + e podlega ocenie i weryfikacji merytorycznej i statystycznej. Ocena merytoryczna polega na sprawdzeniu czy jest on zgodny z teorią ekonomiczną.
Ocena statystyczna obejmuje:
Ocena dopasowania do danych empirycznych dokonywana jest na podstawie współczynników określonych już przy okazji modelu trendu liniowego. Współczynniki te można łatwo liczyć w arkuszu kalkulacyjnym. Liczenie ręczne jest uciążliwe. Wymienimy te współczynniki:
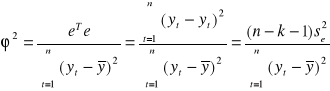
Współczynnik determinacji przyjmuje wartości z przedziału [0, 1], informuje on jaka część całkowitej zmienności zmiennej objaśnianej jest wyjaśniona przez model. Dopasowanie modelu do danych jest tym lepsze im większe jest R2.
Zachodzi równość: ϕ2 + R2 = 1 .
Dopasowanie modelu do danych empirycznych weryfikuje się poprzez weryfikację hipotezy o istotności współczynnika determinacji. Testuje się hipotezę zerową postaci H0 : [R2 = 0] przeciwko hipotezie alternatywnej H1 : [R2 ≠ 0].
Hipotezę testujemy przy pomocy statystyki F Fishera-Snedecora o m1 = k i m2 = (n - k - 1) stopniach swobody, gdzie k to ilość zmiennych objaśniających, n to ilość obserwacji. Hipotezę testujemy na zadanym poziomie istotności γ (np. γ = 0,05).
![]()
Jeśli wykonujemy obliczenia „ręcznie” to dla ustalonego poziomu istotności γ wyznaczamy z tablic wartość krytyczną F* dla m1 , m2 stopni swobody.
Jeśli mamy do dyspozycji arkusz kalkulacyjny Excel to możemy wyznaczyć wartość krytyczną F* przy pomocy funkcji
=ROZKŁAD.F.ODW(γ; m1; m2)
Jeśli F ≤ F* to nie ma podstaw do odrzucenia hipotezy H0 , czyli przyjmujemy, że współczynnik determinacji jest nieistotnie różny od zera. Jeśli F > F* to odrzucamy hipotezę H0 na rzecz hipotezy alternatywnej H1 , współczynnik determinacji jest istotnie różny od zera.
Prognoza punktowa
yPT = b0 + b1·xT1 + … + bk·xTk ;
gdzie xT1 , xT2 , … , xTk to ustalone wartości zmiennych objaśniających w prognozowanym okresie.
Lub w postaci wektorowej:
yPT = c b
gdzie c = [ 1, xT1 , … , xTk ] ; b = [ b0 , b1 , … , bk ] .
Wartość ex ante S(DT) średniego błędu predykcji dla tak wyznaczonej prognozy wyznaczamy:
![]()
Przykład 5.1 (Zeliaś)
W tablicy zebrano dane z ostatnich 11 kwartałów. Yt jednostkowy koszt produkcji (zł/szt), Xt1 wielkość produkcji (tys. szt.), Xt2 wskaźnik przestoju maszyn (%).
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
yt |
100,0 |
99,0 |
98,5 |
98,0 |
97,0 |
98,0 |
97,0 |
97,5 |
96,5 |
96,0 |
96,0 |
xt1 |
90 |
95 |
99 |
100 |
101 |
102 |
102 |
103 |
104 |
103 |
105 |
xt2 |
5,9 |
5,8 |
5,7 |
5,7 |
5,5 |
5,6 |
5,2 |
5,3 |
5,1 |
4,8 |
4,8 |
Na podstawie tych danych oszacujemy liniowy model przyczynowo-skutkowy.
Na poziomie wiarygodności 95% obliczymy prognozy punktowe na trzy kwartały w przód. Prognozy uznamy za dopuszczalne jeśli będą obciążone błędem nie większym niż 5%.
Uwaga
Do wyznaczenia prognozy wielkości Yt na 12, 13, 14 kwartał potrzebne są prognozy Xt1, Xt2 . Uznajemy, że są one łatwe do wyznaczenia.
Xt1 dane jest:
x^t1 = 91,2653 t0,0592
lnProg(xt1) = 4,5138 + 0,059 ln(t)
Xt2 dane jest:
x^t2 = 6,0764 - 0,1127 t
Na tej podstawie wyznaczamy prognozy zmiennych niezależnych.
Obliczenia w arkuszu kalkulacyjnym.
UWAGI O PROGNOZOWANIU
W prognozowaniu zazwyczaj rozróżniamy zmienne objaśniające (X) (egzogeniczne) oraz zmienne objaśniane (Y) (endogeniczne). Budowane modele mogą służyć do prognozy wielkości zmiennych zależnych na podstawie zaobserwowanych lub na podstawie „przewidywanych” wielkości zmiennych niezależnych. W drugim przypadku, musimy zdecydować jakie wielkości X wprowadzimy do modelu. Możemy postąpić na kilka sposobów.
Przypadek pierwszy - modele statyczne, brak zależności od czasu.
Za X wybrać wartość średnią ![]()
, medianę xmed, dominantę xdom:
Możemy również zdecydować się na prognozy wariantowe. Obliczyć wielkości zmiennych zależnych Y dla kilku wartości zmiennych niezależnych X. Zazwyczaj obliczamy wariant pesymistyczny (minimalny), średni (najbardziej prawdopodobny) i optymistyczny (maksymalny).
W wariancie średnim do modelu podstawiamy jako wartości X wartości średnie, mediany lub dominanty.
W wariancie pesymistycznym jako wartości X podstawiamy „najgorsze” (najmniejsze lub największe) wielkości z „punktu widzenia” zmiennej zależnej Y. Tymi „najmniejszymi” wartościami mogą być:
Przykład
Model był budowany na podstawie zaobserwowanych wartości X: 9, 12, 9, 12, 6, 12, 14, 9, 15, 12. Dla wygody uporządkujmy obserwacje X rosnąco: 6, 9, 9, 9, 12, 12, 12, 12, 14, 15.
xmin = 6; xmax = 15;
Q1 = 9; xmed = 12; Q3 = 12;
xdom = 12
![]()
; s(x) = 2,708
![]()
; ![]()
![]()
; ![]()
Często, aby ocenić dla jakich wartości X powinniśmy zbudować prognozy wariantowe, badamy postać rozkładu przyjmowanych przez X wartości.
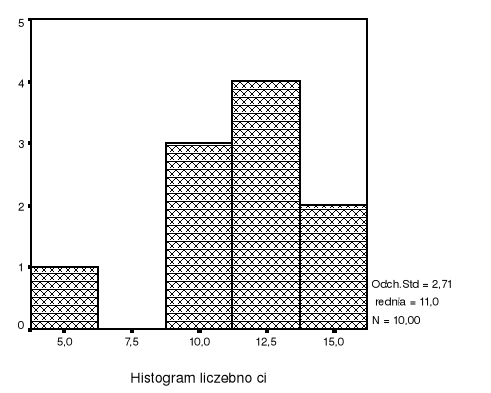
Histogram jest graficznym przedstawieniem rozkładu badanej cechy. Podstawy słupków histogramu są rozłącznymi przedziałami pokrywającymi cały zakres zmienności cechy. Ustalenie szerokości podstaw oraz początku pierwszej podstawy nie jest zdeterminowane. Wysokość słupka w histogramie liczebności odpowiada obserwacji X-ów mieszczących się w przedziale podstawy słupka. Obserwacja histogramu pozwala ocenić jak wygląda rozkład cechy: czy jest symetryczny, skośny, skoncentrowany na jakiś wartościach. Histogram może być wskazówką jakie wartości X powinny być brane pod uwagę przy budowaniu prognoz wariantowych.
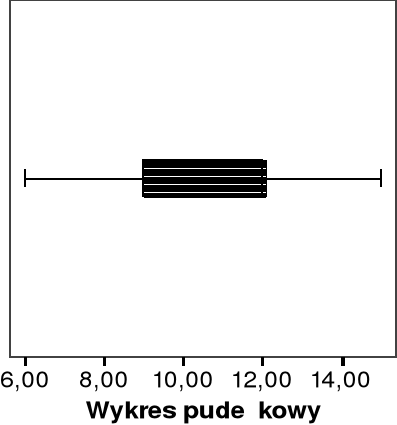
Wykres pudełkowy jest innym sposobem prezentacji danych pomocnym przy ocenie rozkładu cechy i podjęciu decyzji jakie wartości zmiennej niezależnej X powinny być wzięte pod uwagę przy budowaniu prognoz wariantowych.
Przypadek drugi - modele dynamiczne, uwzględniona zależność od czasu.
Częstym przy analizie zjawisk zmieniających się w czasie stosujemy szeregi czasowe. Rozróżniamy szeregi czasowe momentów, gdy obserwowane zjawisko ma charakter zasobu np.: wielkość stopy procentowej 24 maja 2003r, liczba mieszkańców Warszawy w dniu 1 stycznia 2003 roku, cena m2 powierzchni mieszkalnej w dniu 10 listopada 2002r, oraz szeregi czasowe okresów, gdy obserwowane zjawisko ma charakter strumienia np.: sprzedana powierzchnia mieszkaniowa w trzecim kwartale 2002r, liczba nowych mieszkańców Warszawy w kwietniu 2003r. Strumienie mają charakter addytywny. Dodając liczbę sprzedanej powierzchni mieszkaniowej z trzeciego i czwartego kwartału 2002r dostanę liczbę powierzchni mieszkaniowej sprzedanej w drugim półroczu 2002r.
Budując model dynamiczny lub analizując dynamikę zjawiska możemy mieć na celu:
Analiza zmienności zjawiska w czasie.
Proste miary zmienności - przyrosty absolutne:
Przyrosty absolutne informują o bezwzględnej zmianie, wyrażane są w tej samej jednostce co analizowane zjawisko.
Proste miary zmienności - przyrosty względne (tempa, stopy). Wyrażane są przez stosunek przyrostu bezwzględnego do odpowiedniej podstawy:
Przyrosty względne informują o względnej zmianie poziomu zjawiska w dwu kolejnych momentach lub okresach, wyrażanej zazwyczaj procentowo.
Proste miary zmienności - indeksy (wskaźniki dynamiki). Poziom zjawiska w danym momencie lub okresie odnosimy do poziomu lub momentu przyjętego za podstawę.
Indeksy wyrażają procentowe zmiany poziomu zjawiska. Indeks równy 1 oznacza, że poziom zjawiska się nie zmienił. Mniejszy od 1 oznacza spadek, większy wzrost.
W długofalowych zjawiskach stosujemy zazwyczaj wymieniony miary o podstawie stałej, w krótko lub średnio okresowych zjawiskach stosujemy zazwyczaj mierniki łańcuchowe.
Rok |
Wydatki |
Przyrosty absolutne o podstawie stałej |
Przyrosty absolutne o podstawie zmiennej |
Przyrosty względne o podstawie stałej |
Przyrosty względne o podstawie zmiennej |
Indeksy o podstawie stałej |
Indeksy o podstawie zmiennej |
1996 |
530 |
0 |
|
0% |
|
1,00 |
|
1997 |
560 |
30 |
30 |
6% |
6% |
1,06 |
1,06 |
1998 |
590 |
60 |
30 |
11% |
5% |
1,11 |
1,05 |
1999 |
570 |
40 |
-20 |
8% |
-3% |
1,08 |
0,97 |
2000 |
560 |
30 |
-10 |
6% |
-2% |
1,06 |
0,98 |
2001 |
580 |
50 |
20 |
9% |
4% |
1,09 |
1,04 |
2002 |
610 |
80 |
30 |
15% |
5% |
1,15 |
1,05 |
W analizie dynamiki często badamy średni (przeciętny) poziom zjawiska w czasie.
W przypadku zasobu przeciętny poziom wyrażamy średnią chronologiczną:
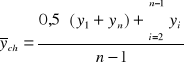
W przypadku strumienia przeciętny poziom wyrażamy średnią arytmetyczną:
![]()
Zarówno dla zasobów, jak i strumieni, gdy badamy średnie (przeciętne) tempo zmian zjawiska w czasie, często stosujemy średnią geometryczną:
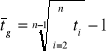
gdzie ti - tempo zmian w chwili lub okresie i.
Dla indeksów łańcuchowych średnia geometryczna sprowadza się do:
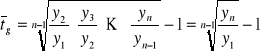
Cd obliczeń do przykładu B:
![]()
![]()
Indeksy indywidualne.
Indeksy indywidualne zwane też indeksami prostymi stosujemy w przypadku badania zjawisk jednorodnych.
Przykład C.
Wyznaczanie indywidualnych indeksów: cen, ilości i wartości. |
|||||||||
|
Ilość - q |
Cena zł/m2 - p |
Wartość - w |
Indyw. indeks ilości iq |
Indyw. indeks cen |
Indyw. indeks wartośći iw |
|||
Sprzedana |
2001 |
2002 |
2001 |
2002 |
2001 |
2002 |
|
|
|
pow. biurowa |
350 |
390 |
3 760 |
3910 |
1 316 000 |
1 524 900 |
1,114 |
1,040 |
1,159 |
pow. mieszkalna |
240 |
210 |
3 520 |
3240 |
844 800 |
680 400 |
0,875 |
0,920 |
0,805 |
pow. magazynowa |
320 |
460 |
1 250 |
1520 |
400 000 |
699 200 |
1,438 |
1,216 |
1,748 |
Indeksy agregatowe.
Indeksy agregatowe zwane też indeksami zespołowymi stosujemy w przypadku badania zjawisk niejednorodnych. W rozważaniach, zwłaszcza ekonomicznych, często posługujemy się agregatami jednostek np.: wielkością produkcji wyrażaną przez wartość sprzedaną, produktem krajowym brutto, wielkością usług świadczonych przez firmę usługową itp.
Przykłady:
Agregatowy indeks wartości. W skład zespołu wchodzi n jednostek (produktów, usług…). Wartość agregatu w chwili t określamy zsumowane wartości poszczególnych pozycji w chwili t:
Wt = qt(1)·pt(1) + qt(2)·pt(2) + … qt(m)·pt(m)
gdzie
qt(i) - ilość i-tego produktu w chwili t;
pt(2) - cena i-tego produktu w chwili t.
Agregatowy indeks wartości jest ilorazem odpowiednich agregatowych wartości:
Agregatowy indeks wartości o stałej podstawie:
![]()
Agregatowy indeks wartości o zmiennej podstawie:
![]()
Agregatowy indeks ilości. Ustalając jak wyglądały zmiany ilości dla całego agregatu musimy przyjąć stałość cen w badanym okresie. Najczęściej stosowane agregatowe indeksy ilości to indeksy Lapeyresa i Paaschego.
W indeksie Lapeyresa (oznaczenie IqL) stosujemy stałe ceny na poziomie okresu podstawowego:
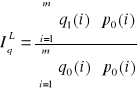
W indeksie Paaschego (oznaczenie IqP) stosujemy stałe ceny na poziomie okresu badanego:
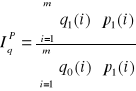
Podobnie określamy agregatowe indeksy cen:
W indeksie Lapeyresa (oznaczenie IpL) stosujemy stałą ilość na poziomie okresu podstawowego:
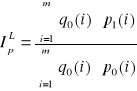
W indeksie Paaschego (oznaczenie IpP) stosujemy stałą ilość na poziomie okresu badanego:
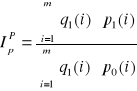
Przykład cd przykładu C:
Wyznaczanie indywidualnych indeksów: cen, ilości i wartości. |
|
||||||||
Sprzedana |
q0 |
q1 |
p0 |
p1 |
q0*p0 |
q1*p1 |
q1*p0 |
q0*p1 |
|
pow. biurowa |
350 |
390 |
3 760 |
3910 |
1 316 000 |
1 524 900 |
1 466 400 |
1 368 500 |
|
pow. mieszkalna |
240 |
210 |
3 520 |
3240 |
844 800 |
680 400 |
739 200 |
777 600 |
|
pow. magazynowa |
320 |
460 |
1 250 |
1520 |
400 000 |
699 200 |
575 000 |
486 400 |
|
|
|
|
|
|
|
|
|
|
|
(q1*p1 / q0*p0) |
|
IW = |
1,748 |
Agregatowy indeks wartości |
|
||||
(q1*p0 /q0*p0 ) |
|
IqL = |
1,438 |
Agregatowy indeks ilości Laspeyresa |
|||||
(q1*p1 /q0*p1 ) |
|
IqP = |
1,438 |
Agregatowy indeks ilości Paaschego |
|||||
(q0*p1 /q0*p0 ) |
|
IpL = |
1,216 |
Agregatowy indeks ceny Laspeyresa |
|||||
(q1*p1 /q1*p0 ) |
|
IpP = |
1,216 |
Agregatowy indeks ceny Paaschego |
|||||
Analiza przyczyn zmienności zjawiska w czasie.
Przedstawione dotychczas metody analizy indeksowej pozwoliły odpowiedzieć na pytanie jak dane zjawisko zmieniało się w czasie. Obecnie skupimy się nad analizą przyczyn zmienności w czasie. Zazwyczaj staramy się wyodrębnić trzy czynniki:
Wyodrębnienie każdego z powyższych czynników nosi nazwę dekompozycji szeregu czasowego. Dekompozycja może być wykonywana metodą:
Wykład 5
Prognozowanie zjawisk jakościowych
Dotychczas zajmowaliśmy się prognozowaniem zjawisk ilościowych. Teraz zajmiemy się zjawiskami, w których występują zmienne jakościowe. Zmienne jakościowe przyjmują skończoną lub przeliczalną ilość stanów. Skupimy się na najprostszym przypadku dwóch wartości i przypiszemy im wartości numeryczne: 0 i 1.
Jeśli tak określona zmienna jest zmienną objaśniającą to postępujemy jak w dotychczasowych modelach. Zero-jedynkową zmienną objaśniającą traktujemy jak zmienną ilościową. Nie możemy tak jednak postąpić, w przypadku zmiennej objaśnianej ze względu na to, że przyjmuje ona tylko określone wartości.
Zapoznamy się z dwoma typami metod ekonometrycznych modelowania i prognozowania zmiennych jakościowych.
Pierwszy skupia się na wyznaczaniu rozkładu prawdopodobieństw możliwych wyników zmiennej objaśnianej.
Druga skupia się na określaniu reguł dyskryminacyjnych przypisywania obiektów populacji do różnych kategorii.
Typ pierwszy: określanie rozkładu prawdopodobieństwa
Y zmienna objaśniana zero-jedynkowa.
P(Y=1) = p; P(Y=0) = q; p + q = 1.
Wiemy, że zachodzi zależność:
E(Y) = 1·p + 0·q = p
Będziemy budować model określający wartość oczekiwaną zmiennej Y:
F( 0 + 1·X1+ 2·X2+ … + k·Xk + ) = E(Y) = p
Gdzie zmienne X1, … Xk zmienne objaśniające; 0, 1,… k· parametry; skałdnik losowy. F funkacja rosnąca.
Oszacowanie prawdopodobieństwa p dostajemy z oszacowania postaci:
pi^ = F( b0 + b1·xi1+ b2·xi2+ … + bk·xik ); i = 1, 2, … n ;
gdzie xi1, … xik występujące wartości zmiennych objaśniających, b1, … bk oszacowania parametrów.
W zależności od postaci funkcji F wyróżnimy trzy modele: liniowy, probitowy, logitowy.
Model liniowy
p = 0 + 1·X1+ 2·X2+ … + k·Xk + ;
Wygodny w użyciu, łatwy di interpretacji, ale dający wadliwe oceny parametru p, nie należące do przedziału [0, 1].
Model probitowy
p = ( 0 + 1·X1+ 2·X2+ … + k·Xk + ) ;
gdzie jest dystrybuantą standardowego rozkładu normalnego N(0, 1).
Wartości -1(p) nazywa się normitami. Wartości
Pr = -1(p) + 5 = -1( P(Y = 1) ) + 5
nazywa się probitami.
Wygodny jest liniowy model probitowy:
Pr = 0 + 1·X1+ 2·X2+ … + k·Xk + ;
Postępujemy standardowo. Szacujemy parametry modelu, sprawdzamy stopień dopasowania do obserwacji empirycznych i jeśli jest zadowalający to możemy prognozować wartość probitu. Na podstawie oszacowanej wartości probitu określamy oszacowanie prawdopodobieństwa p:
p = ( Pr - 5 )
Model probitowy zakłada, że kombinacja liniowa zmiennych objaśniających ma rozkład normalny N(0,1).
Model logitowy
Zakładamy, że F jest dystrybuantą rozkładu logistycznego:
![]()
Wartości funkcji odwrotnej do F nazywamy logitami i oznaczamy przez L:
L = ln( p / q )
Oczywiście q = 1 - p .
Jeśli p = q , to L=0. Jeśli p > q , to L > 0. Jeśli p < q , to L < 0.
Oczywiście zachodzi:
p = F(L) = exp( L ) / (1 + exp( L ))
Wygodny jest liniowy model logitowy:
L = 0 + 1·X1+ 2·X2+ … + k·Xk + ;
Parametry modelu probitowego i logitowego szacujemy uogólnioną metodą najmniejszych kwadratów. Ze wzorów:
b = (XT V-1 X)-1 XT V-1 Pr
b = (XT V-1 X)-1 XT V-1 L
gdzie:
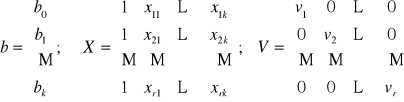
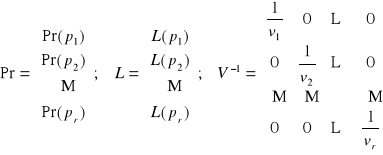
vi - to oszacowanie wariancji składników losowych. To oszacowanie jest różne w tych dwóch modelach.
W modelu probitowym stosujemy oszacowanie:
![]()
W modelu logitowym stosujemy oszacowanie:
![]()
gdzie:
pi jest częstością w i-tej grupie obserwacji, czyli pi = ( mi / ni ), ni - to ilość wszystkich obserwacji w i-tej grupie, zaś mi - to ilość obserwacji w których Y = 1.
Prognozowanie za pomocą modeli dyskryminacyjnych
Celem analizy dyskryminacyjnej jest stworzenie modelu umożliwiającego klasyfikowanie badanych obiektów do jednej z dwu kategorii. Analiza dyskryminacyjna składa się z dwóch etapów.
Etap pierwszy to dyskryminacja, „uczenie się”, mamy poprawnie sklasyfikowane obiekty, badamy ich charakterystyki i budujemy funkcję dyskryminacji.
Etap drugi to klasyfikacja przy pomocy zbudowanej funkcji dyskryminacji.
Oznaczenia przyjmujemy jak poprzednio: Y zero-jedynkowa, X1, …, Xk zmienne objaśniające.
Wykonujemy r obserwacji uczących, czyli mamy r punktów w k-wymiarowej przestrzeni. Te r punktów klasyfikujemy do dwóch zbiorów: {Y=1} i {Y=0}. Znajdujemy teraz hiperpłaszczyznę rozdzielająca te dwa zbiory (jeśli to jest możliwe).
Funkcja dyskryminacji liniowej ma postać: f(X) = 1X1 + … + kXk .
Wektor b ocen parametrów wyznaczamy z równania:
b = C-1 m
gdzie:
C = C(0) + C(1) ; m = m(1) - m(0)
C(i) - to macierz oszacowań kowariancji wektorów z i-tej grupy.
m(i) - to wektor oszacowań k wymiarowych średnich z i-tej grupy.
f0 - wartość decyzyjna, wartości większe klasyfikujemy do jednej grupy, mniejsze do drugiej.
f0 = ( fśr^(0) + fśr^(1) ) / 2
gdzie
fśr^(i) to średnia arytmetyczna z wartości teoretycznych funkcji dyskryminacji dla obserwacji należących do i-tej grupy.
PiS wykład 1-5.doc Prognozowanie i symulacje
P. Zaremba 37/37
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
1533
1533
1533
Webasto Programator Cyfrowy 1533 Instrukcja Obsługi
webasto 1533
więcej podobnych podstron