WYDZIAŁ ELEKTRONKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA METROLOGII I SYSTEMÓW ELEKTRONICZNYCH LABORATORIUM METROLOGII I TECHNIKI EKSPERYMENTU GRUPA 4A
Ćwiczenie nr 2 Pomiary oscyloskopowe	Imię i nazwisko	Dariusz Kos
		Data wykonania ćwiczenia	08.03.2005
		Data odbioru sprawozdania	15.03.2005
		Ocena zaliczenia
		Uwagi i podpis

Sprawozdanie

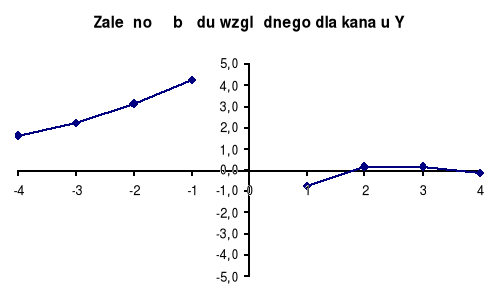
7.4.1. Wzorcowanie kanału Y oscyloskopu napięciem stałym

Celem tego zadania było wyznaczenie metodą najmniejszych kwadratów stałej napięciowej kanału Y poprzez odchylanie plamki stałym napięciem o określoną liczbę działek. Poniższa tabela zawiera wyniki poszczególnych pomiarów i obliczeń.

Tablica 7.1

y	cm	1	2	3	4	-4	-3	-2	-1
Uy	V	0,978	1,973	2,960	3,936	-4,002	-3,020	-2,032	-1,027
Dypom	V/cm	0,978	0,987	0,987	0,984	1,001	1,007	1,016	1,027
δD	%	-1,7	-0,8	-0,8	-1,1	0,6	1,2	2,1	3,2
Dyobl	V/cm	0,995

7.4.2. Pomiary współczynnika wypełnienia przebiegu prostokątnego

Celem tego zadania było wyznaczenie współczynnika wypełnienia przebiegu prostokątnego na podstawie obrazu jednego okresu tego sygnału. Wartość znamionowa okresu impulsu wynosiła 600μs, a wartości znamionowe czasów trwania impulsu - 120μs, 480μs. Po określeniu odpowiednich wymiarów impulsu na ekranie oscyloskopu (x_T, x_tw1, x_tw2) i uwzględnieniu współczynnika podstawy czasu (0,1 ms/cm) wyznaczyliśmy rzeczywisty okres impulsu (T) oraz rzeczywiste czasy trwania impulsu (t_w1, t_w2). Następnie za pomocą poniższego wzoru otrzymaliśmy współczynniki wypełnienia (k₁, k₂):

Tablica 7.2

xT	cm	6,1
xtw1	cm	1,2
xtw2	cm	4,8
T	μs	610
tw1	μs	120
tw2	μs	480
k1	%	19,7
k2	%	78,7

Uwagi:

Różnica między znamionową wartością okresu impulsu a rzeczywistą (w tym przypadku ΔT = 10μs) może wynikać z niestabilności generatora (np. wydłużenie czasu przełączenia między stanem niskim i wysokim).

7.4.3. Pomiary napięcia i czasu oscyloskopem

Celem tego zadania było wykonanie pomiarów napięć i czasu na układzie całkującym, a następnie wyznaczenie jego stałej czasowej. Do układu podawany był przebieg prostokątny o okresie 600μs i wypełnieniu 50%. Do obliczeń wykorzystaliśmy poniższy wzór:

Z powyższego wzoru wyznaczamy wartość stałej czasowej:

Parametry układu całkującego: R=1kΩ, C=208nF

Tablica 7.3

U(t1)	V	3,200
U(t2)	V	0,720
t	μs	304
RCteor	μs	208
RCpom	μs	204
δRC	%	-2,0

Uwagi:

Błędy przy wyznaczaniu stałej czasowej mogą wynikać z niestabilności sygnału z generatora (w poprzednim zadaniu pokazaliśmy, że znamionowa wartość okresu tego przebiegu różniła się od rzeczywistej).

7.4.4. Różnicowe pomiary napięć między dwoma punktami nieuziemionymi

W zadaniu tym należało wykorzystać sumacyjny tryb pracy oscyloskopu, gdyż bezpośrednie badanie dwóch punktów, z których żaden nie jest połączony z masą, spowodowałoby zmianę konfiguracji układu. Poniższa tabela zawiera wyniki pomiarów.

Tablica 7.4

U(t1)	V	3,120
U(t2)	V	0,760
t	μs	304
RCteor	μs	208
RCpom	μs	215
δRC	%	3,4

7.4.5. Automatyczne pomiary parametrów przebiegu okresowego

Celem tego zadania było wyznaczenie za pomocą automatycznego trybu pracy oscyloskopu następujących parametrów przebiegu prostokątnego:

V_pp - napięcie międzyszczytowe

V_rms - napięcie skuteczne

V_avg - napięcie średnie

f - częstotliwość

T - okres

t_w - czas trwania dodatnich impulsów

k - współczynnik wypełnienia

Tablica 7.5

Vpp	V	4,200
Vrms	V	1,840
Vavg	V	0,800
f (F)	Hz	1,667
T	μs	600
tw (W+)	μs	120
k (DC+)	%	20

Uwagi:

W tym zadaniu wyniki pomiarów zostały wyznaczone przez sam oscyloskop, dzięki czemu nie wprowadziliśmy błędu pomiarowego związanego z odczytem wartości z wykresu na ekranie oscyloskopu.

7.4.6. Obserwacja przebiegów w układach cyfrowych

Celem tego zadania była obserwacja przebiegów w liczniku binarnym SN7493 oraz na bramce AND 7408. Wyznaczyliśmy, ile okresów przebiegu wejściowego T_in przypada na jeden okres przebiegów na poszczególnych wyjściach licznika T_A, T_B, T_C, T_D:

T_A = 2 × T_in ,

T_B = 4 × T_in ,

T_C = 8 × T_in ,

T_D = 16 × T_in ,

Zmierzyliśmy również poziomy napięć na wyjściu A:

U_Hi = 3,920V.

U_Lo = 0,000V,

Przy badaniu bramki AND zaobserwowaliśmy, że jest ona otwarta, gdy na wejściu IN1 jest sygnał wysoki, a zamknięta, gdy na wejściu IN1 jest sygnał niski.

7.4.7. Pomiary parametrów impulsów w przebiegu okresowym

Celem tego zadania był pomiar za pomocą automatycznego trybu pracy oscyloskopu następujących parametrów impulsów:

t_r - czas narastania

t_f - czas opadania

t_w - czas trwania

T - okres

Tablica 7.6

tr	μs	32
tf	μs	16
tw (W+)	μs	296
T	μs	1200

7.4.8. Pomiary parametrów pojedynczego impulsu z wykorzystaniem pracy cyfrowej

W tym zadaniu do wykonania pomiarów niezbędny jest oscyloskop z funkcją pamięci, gdyż pojedyncze impulsy ze względu na krótki czas trwania są niemożliwe do zaobserwowania przy pomocy klasycznego oscyloskopu analogowego bez pamięci.

Po ustawieniu oscyloskopu w cyfrowy tryb pracy z pojedynczym wyzwalaniem, wygenerowaliśmy na jego wejście pojedynczy impuls i uzyskaliśmy następujące wyniki:

t_w = 280μs (czas trwania)

U_Hi = 3,720V (poziom napięcia dla stanu wysokiego)

7.4.9. Obserwacja charakterystyk diod półprzewodnikowych I = f (U) w obszarze przewodzenia

W zadaniu tym należało wytworzyć na ekranie oscyloskopu charakterystyki prądowonapięciowe poszczególnych diod, a następnie wyznaczyć wartości poniższych wielkości dla prądu przewodzenia

I = 25mA:

U - napięcie przewodzenia

- rezystancja statyczna w obszarze przewodzenia

- rezystancja dynamiczna w obszarze przewodzenia

Tablica 7.7

typ diody	U [V]	R []	ΔU [V]	ΔI [mA]	rd []
germanowa	0,31	12,4	0,10	52	19,23
krzemowa	0,71	28,4	0,12	38	31,67
LED	2,52	100,8	0,5	45	111,11

Uwagi:

W wynikach pomiarów występuje niewielki błąd, który spowodowany jest faktem, że w układzie pomiarowym w celu zamiany prądu na napięcie zastosowany został rezystor, który wprowadzał niewielkie zniekształcenie charakterystyk.

Dioda

germanowa

Dioda

krzemowa

Dioda

LED

4

Tryb: XY

CH1 (X)= 0,1 V/cm

CH2 (Y) = 10 mV/cm

Tryb: XY

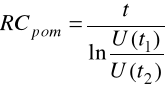
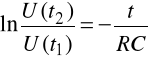
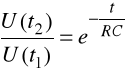
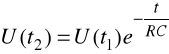
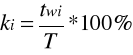
CH2 (Y) = 10 mV/cm

CH1 (X)= 0,1 V/cm V/cm

Tryb: XY

CH2 (Y) = 10 mV/cm

CH1 (X)= 0,5 V/cm

---