2

2

4

T

L

g

π

=

LABORATORIUM FIZYKI

Ć

wiczenie 2

„Drgania proste harmoniczne: wahadło rewersyjne i wahadło torsyjne.”

Wydział Mechatroniki
Alicja Zieli

ń

ska; grupa 25; zespół 1

1. Wst

ę

p.

Ć

wiczenie składało si

ę

z dwóch cz

ęś

ci. Pierwsza z nich miała na celu wyznaczenie

warto

ś

ci przyspieszenia ziemskiego za pomoc

ą

wahadła rewersyjnego na podstawie

okresów jego drga

ń

. Warto

ść

t

ą

wyznaczamy ze wzoru:

Druga cz

ęść

polegała na wyznaczeniu modułu sztywno

ś

ci za pomoc

ą

wahadła

torsyjnego na podstawie pomiaru okresu jest drga

ń

. Warto

ść

modułu wyznaczamy ze

wzoru:

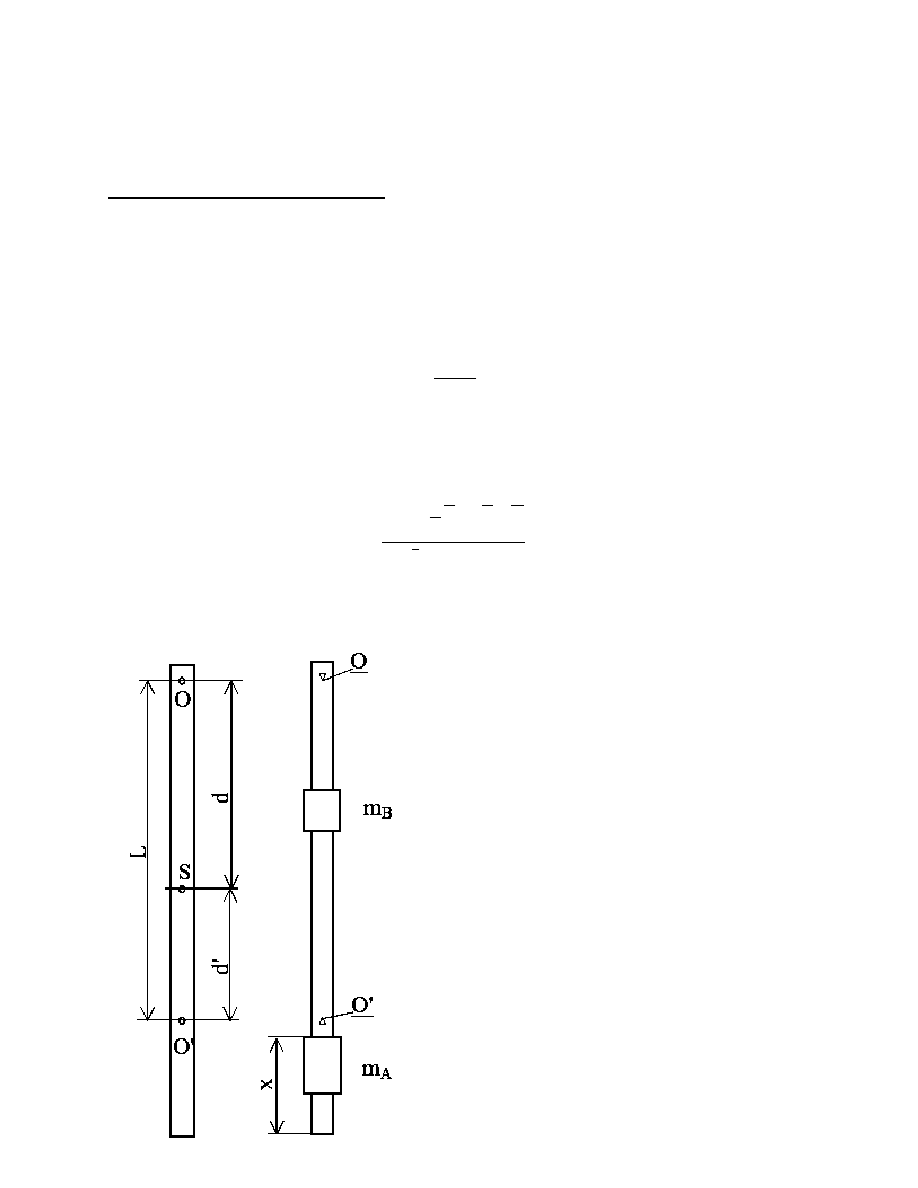
2. Układ pomiarowy.

Układ pomiarowy warto

ś

ci przyspieszenia

ziemskiego składał si

ę

z wahadła torsyjnego o

dwóch osiach. Odległo

ść

mi

ę

dzy osiami

wynosiła L. Pomi

ę

dzy osiami znajdował si

ę

ci

ęż

arek m

B

. W zało

ż

eniu

ć

wiczenia miał on

by

ć

ruchomy jednak

ż

e prowadz

ą

cy

ć

wiczenia

postanowili ułatwi

ć

wykonanie

ć

wiczenia i

ustawili ci

ęż

arek w odpowiednim poło

ż

eniu.

Ponad osi

ą

O’ znajdował si

ę

ruchomy ci

ęż

arek

m

A

.

(

)

2

1

2

2

4

2

2

2

1

8

T

T

r

m

d

R

L

n

G

−













+

=

π

Układ pomiarowy wyznaczania modułu
spr

ęż

ysto

ś

ci składał si

ę

z wahadła torsyjnego i n

ci

ęż

arków umieszczanych na sztyftach wahadła.

3. Wykonanie

ć

wiczenia.

I.

Wahadło rewersyjne.

Ci

ęż

arek m

B

, jak wspomniałam wcze

ś

niej, został ju

ż

ustawiony w odpowiedniej pozycji

przez prowadz

ą

cych tak

ż

e nie musieli

ś

my wykonywa

ć

tej cz

ęś

ci

ć

wiczenia z

ustawianiem tego

ż

ci

ęż

arka.

1. Ustawiamy ci

ęż

arek m

A

w poło

ż

eniu najbli

ż

szym osi O’.

2. Mierzymy czas 20 wahni

ęć

wokół osi O i wyznaczamy okres drga

ń

T

O

.

3. Odwracamy wahadło i mierzymy czas 20 wahni

ęć

wokół osi O’. Wyznaczamy okres

drga

ń

T

O’

.

4. Przesuwamy ci

ęż

arek m

A

o 2cm.

5. Powtarzamy czynno

ś

ci 2-4 do momentu, gdy ci

ęż

arek znajdzie si

ę

na ko

ń

cu

wahadła.

6. Sporz

ą

dzamy wykresy T

O

(x) i T

O’

(x). Znajdujemy punkt, w którym T

O

= T

O’

czyli

punkt przeci

ę

cia si

ę

wykresów: (x

0

,T).

7. Mierzymy odległo

ść

L mi

ę

dzy osiami. Otrzymane warto

ś

ci T i L podstawiamy do

wzoru podanego we wst

ę

pie, obliczamy warto

ść

przyspieszenia ziemskiego.

Wyznaczamy bł

ę

dy obliczonej warto

ś

ci. Porównujemy wynik z warto

ś

ciami

tablicowymi.

II.

Wahadło torsyjne

1. Mierzymy

ś

rednic

ę

(2r) i długo

ść

(L) badanego pr

ę

ta.

2. Wprawiamy w ruch wibrator z obci

ąż

eniem wst

ę

pnym, mierzymy czas t

1

dwudziestu

okresów drga

ń

.

3. Mierzymy

ś

rednice (2R) i wa

ż

ymy n dodatkowych ci

ęż

arków oraz odległo

ść

mi

ę

dzy

sztyftami (2d), na których umieszczamy owe ci

ęż

arki.

4. Ponownie wprawiamy wibrator w drgania, mierzmy czas t

2

dwudziestu okresów

drga

ń

.

5. Wyznaczamy warto

ś

ci T1 i T2, obliczamy warto

ś

ci

ś

rednie r, R, D, m.

6. Wyznaczamy wielko

ść

G ze wzoru podanego we wst

ę

pie. Obliczmy bł

ę

dy,

porównujemy wynik z warto

ś

ci

ą

tablicow

ą

.

2

2

2

2

2

2

9,97456

16

,

2

18

,

1

*

14

,

3

*

4

4

s

m

s

m

T

L

g

=

=

=

π

4. Wyniki i ich opracowanie.

I.

Wahadło rewersyjne.

L [cm] = 118

n =

20

x [cm]

0

2

4

6

8

10

12

14

16

t

0

[s]

38,32

39,37

40,12

40,81

41,21

42,12

42,72

43,32

44,48

T

0

[s]

1,916

1,9685

2,006

2,0405

2,0605

2,106

2,136

2,166

2,224

t

0

' [s]

41,84

42,06

42,1

42,44

42,57

42,72

42,97

43,21

43,38

T

0

' [s]

2,092

2,103

2,105

2,122

2,1285

2,136

2,1485

2,1605

2,169

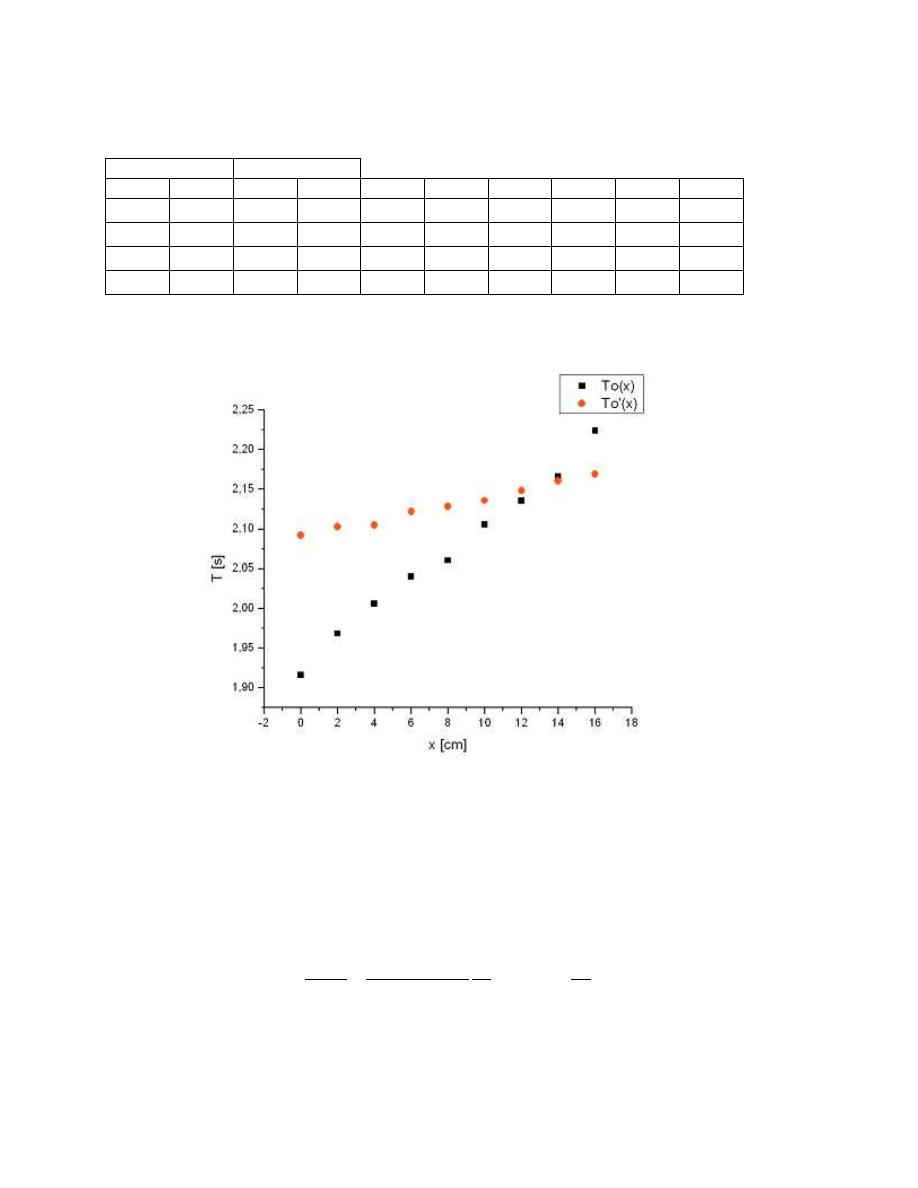
Tabela 1. Wyniki pomiarów okresu drga

ń

.

Wykres zale

ż

no

ś

ci okresu drga

ń

wahadła od poło

ż

enia ci

ęż

arka m

A

.

Punkt przeci

ę

cia si

ę

dwóch prostych b

ę

d

ą

cych przybli

ż

eniami funkcji To(x) i

To’(x) jest równy (13,39 ; 2,16). Warto

ść

odczytana przy pomocy funkcji Screen Reader

programu Origin.

Ze wzoru podanego we wst

ę

pie obliczamy warto

ść

przyspieszenia ziemskiego:

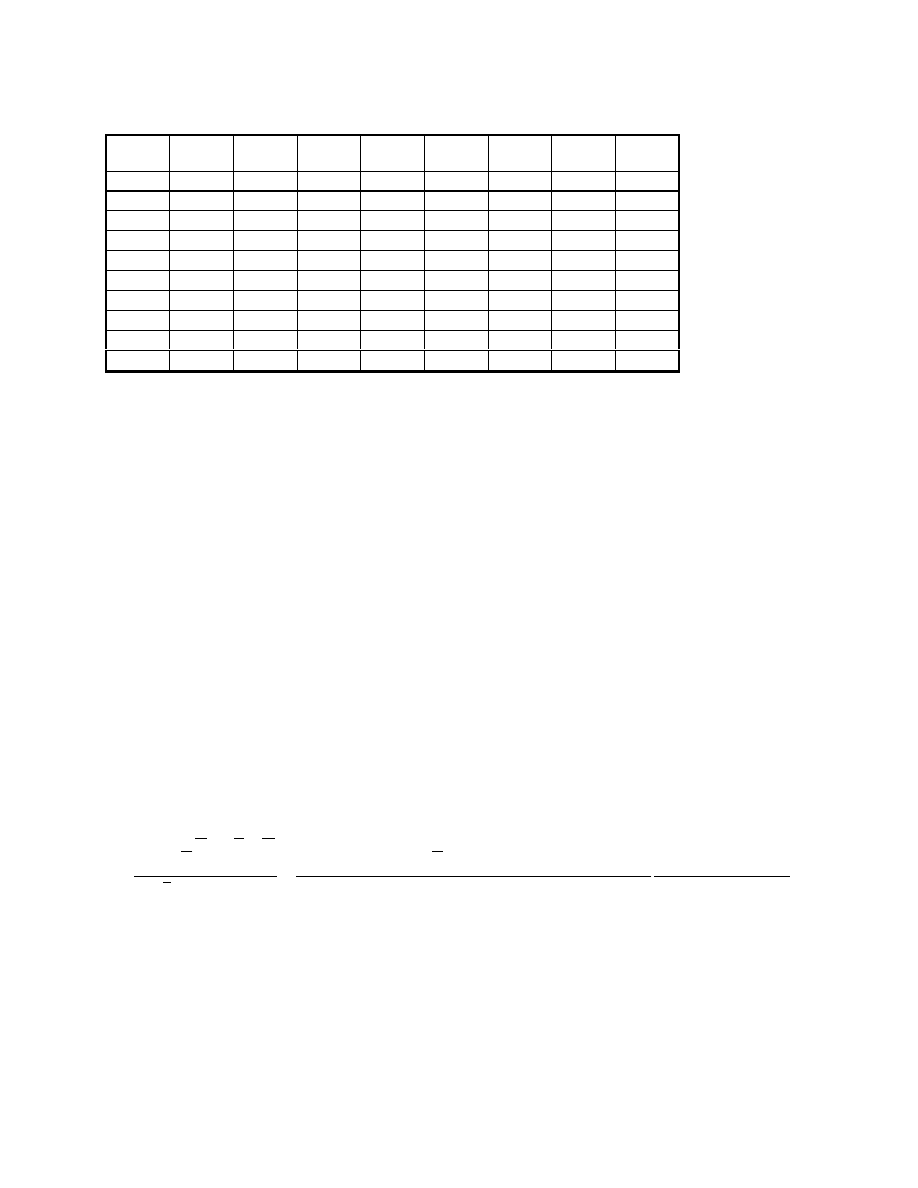
II.

Wahadło torsyjne.

2r [mm] L [cm]

2R
[mm]

m [g]

d [cm]

t1 [s]

t2 [s]

T1 [s]

T2[s]

3,59

88,5

24,94

21

8,75

21,19

0,4375

1,0595

3,59

88,4

24,95

192,5

21,2

8,75

21,21

0,4375

1,0605

3,59

88,4

24,98

21,1

8,84

21,19

0,442

1,0595

3,57

88,4

24,97

190,5

21,2

8,78

21,15

0,439

1,0575

3,6

88,5

24,96

8,75

21,19

0,4375

1,0595

3,59

24,94

183

3,58

24,98

3,58

24,99

184,2

3,59

3,6

Tablela 2. Wyniki pomiarów wahadła torsyjnego.

Wyznaczamy warto

ś

ci

ś

rednie:

Obliczamy warto

ść

modułu sztywno

ś

ci:

4

2113

,

0

125

,

21

188

,

0

55

,

187

0125

,

0

5

,

12

844

,

8

44

,

88

0018

,

0

8

,

1

0593

,

1

4387

,

0

T

2

1

=

≈

=

≈

=

=

≈

=

=

=

≈

=

=

n

m

cm

d

kg

g

m

m

mm

R

m

cm

L

m

mm

r

s

T

s

(

)

(

)

Pa

s

s

m

kg

m

m

m

T

T

r

m

d

R

L

n

G

11

2

2

4

2

2

2

2

4

2

2

2

1

2

2

4

2

2

10

*

68

,

7

)

(

*

*

)

(

*

4387

,

0

0593

,

1

0018

,

0

188

,

0

*

2113

,

0

0125

,

0

*

2

1

844

,

8

*

14

,

3

*

4

*

8

2

1

8

=

=

−

+

−













+

=

−













+

=

π

( )

(

)

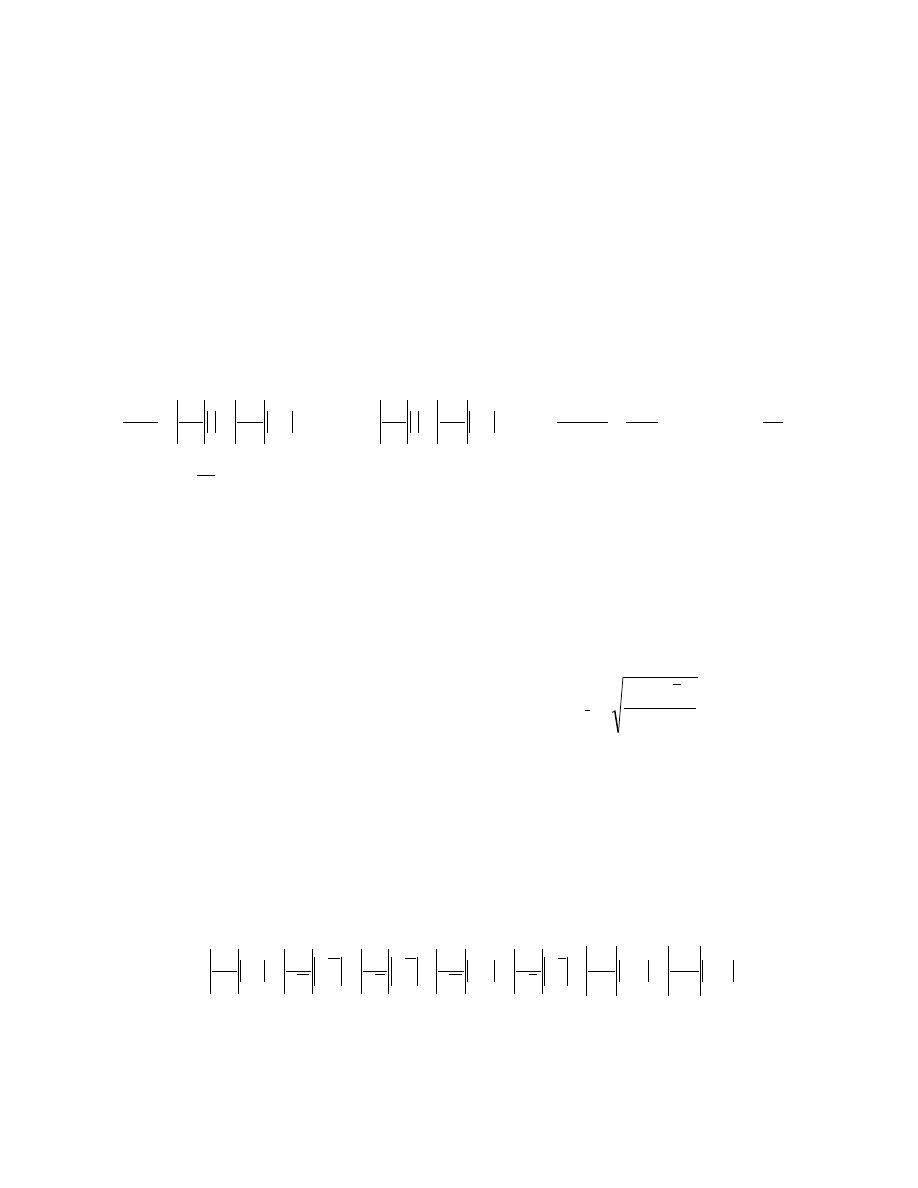
1

2

−

−

Σ

=

n

n

x

x

s

i

x

5. Rachunek bł

ę

dów.

I.

Wahadło rewersyjne.

Maksymalne bł

ę

dy bezwzgl

ę

dne wielko

ś

ci mierzonych bezpo

ś

rednio [w naszym

przypadku s

ą

to: długo

ść

zredukowana wahadła rewersyjnego (L) oraz okres drga

ń

tego

ż

wahadła (T)] mo

ż

na wyznaczy

ć

z odległo

ś

ci pomi

ę

dzy działkami przedmiotu.

Z tego wynika,

ż

e

∆

L = ± 0,5mm, poniewa

ż

odległo

ść

mi

ę

dzy działkami na

miarce wynosi 1mm; jeste

ś

my w stanie odczyta

ć

wynik z dokładno

ś

ci

ą

do połowy

działki.

Bł

ą

d pomiaru okresu drga

ń

mo

ż

emy przyj

ąć

,

ż

e wynosi

∆

T = ± 0,2s wynikaj

ą

cy z

niedokładno

ś

ci obserwatora (za pó

ź

no lub za szybko mógł zatrzymywa

ć

stoper).

Bezwzgl

ę

dny bł

ą

d maksymalny przyspieszenia ziemskiego g zale

ż

nego od L i T

obliczamy za pomoc

ą

metody pochodnej logarytmicznej:

g = 9,97 ± 1,85 m/s

2

II.

Wahadło torsyjne.

Bł

ę

dy warto

ś

ci zmierzonych bezpo

ś

rednio przyjmujemy jak przy wahadle rewersyjnym:

∆

L = ± 0,5 mm = ±0,0005 m;

∆

T

1

=

∆

T

2

= ± 0,2 s;

Ś

rednie bł

ę

dy warto

ś

ci

ś

rednich obliczamy ze wzoru:

∆

r = ± 0,57 m;

∆

R = ± 7,65 * 10

-6

m;

∆

m = ± 0,0023 kg;

∆

d = ± 0,00048 m;

(prosz

ę

wybaczy

ć

mi brak zapisu wszystkich oblicze

ń

po kolei ale z powodu

ś

wi

ę

ta Politechniki Warszawskiej i przesuni

ę

cia terminu

laboratoriów mieli

ś

my mniej czasu na przygotowanie sprawozdania)

Bezwzgl

ę

dny bł

ą

d maksymalny modułu sztywno

ś

ci obliczamy metod

ą

ró

ż

niczki

zupełnej ze wzoru:

G = 76,8 ± 1,5 GPa

2

2

s

m

1,85137

97456

,

9

*

2

*

16

,

2

2

,

0

18

,

1

0005

,

0

*

2

1

2

1

=

=













+

=













−

∆

+

∆

=

∆

⇒

−

∆

+

∆

=

∆

s

m

g

T

T

L

L

g

T

T

L

L

g

g

m

m

GPa

Pa

T

T

G

T

T

G

r

r

G

m

m

G

d

d

G

R

R

G

L

L

G

G

m

47

,

1

10

*

47

,

1

10

*

3

10

*

4

,

1

10

*

9

10

*

5

,

9

10

*

5

,

3

10

*

6

,

1

10

*

3

,

4

9

11

11

8

9

9

6

7

2

2

1

1

±

=

±

=

=

−

+

−

+

+

+

=

=

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

=

∆

−

6. Wnioski.

I.

Wahadło rewersyjne.

Z naszych pomiarów i oblicze

ń

uzyskali

ś

my warto

ść

przyspieszenia ziemskiego

g = 9,97 ± 1,85 m/s

2

. W porównaniu z wielko

ś

ci

ą

tablicow

ą

, wynosz

ą

c

ą

9,81 m/s

2

, jest

to bardzo dobry i dokładny wynik. Niepokoi

ć

mo

ż

e jedynie wielko

ść

bł

ę

du, która wynosi

około 18,5 procenta obliczonej przez nas warto

ś

ci g, jednak

ż

e ten zakres bł

ę

du

obejmuje wynik tablicowy.

Uwa

ż

am,

ż

e zastosowana metoda pomiarowa jest poprawna. Mogliby

ś

my

jedynie popracowa

ć

nad zwi

ę

kszeniem jej dokładno

ś

ci poprzez zastosowanie jakiego

ś

czujnika mierz

ą

cego czas wahni

ęć

, który byłby dokładniejszy od człowieka.

II.

Wahadło torsyjne.

Z naszych pomiarów i oblicze

ń

uzyskali

ś

my warto

ść

modułu sztywno

ś

ci G =

76,8 ± 1,5 GPa. W porównaniu z warto

ś

ci tablicow

ą

, wynosz

ą

c

ą

80 GPa, mo

ż

emy

stwierdzi

ć

, i

ż

jest to bardzo dokładny wynik. Niestety, warto

ść

tablicowa nie zawiera si

ę

w granicach bł

ę

du naszego pomiaru aczkolwiek jest bardzo blisko nich. Warto

ść

bł

ę

du,

jak

ą

uzyskali

ś

my jest bardzo mała, poniewa

ż

wynosi ona niecałe 2% warto

ś

ci

otrzymanej.

Uwa

ż

am,

ż

e zastosowana metoda pomiarowa jest poprawna. Mieli

ś

my w niej

wi

ę

cej czynników mog

ą

cych wywoływa

ć

bł

ę

dy ni

ż

przy wahadle rewersyjnym (wi

ę

cej

warto

ś

ci mierzonych bezpo

ś

rednio, od których zale

ż

ała warto

ść

mierzona po

ś

rednio) a

jednak otrzymali

ś

my dokładniejszy wynik. Jednak

ż

e nie był to wynik idealny, poniewa

ż

jak ju

ż

zwróciłam uwag

ę

warto

ść

tablicowa nie mie

ś

ciła si

ę

w granicach bł

ę

du.

Propozycj

ę

poprawienia dokładno

ś

ci mam tak

ą

sam

ą

jak przy wahadle rewersyjnym –

zwi

ę

kszy

ć

dokładno

ść

pomiaru okresu wahni

ęć

, poprzez zastosowanie jakiego

ś

czujnika, poniewa

ż

to wła

ś

nie bł

ę

dy pomiaru czasu były najwi

ę

ksze.