Mateusz Szumilas, wydział Mechatroniki, grupa 25, zespół 9
Ć
WICZENIE
32.
W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
d
METODĄ
STATYCZNĄ
1. W
STĘP
Ćwiczenie miało pozwolić na poznanie własności i zasady działania piezoelektryków poprzez
badanie zjawiska piezoelektrycznego prostego oraz odwrotnego. W powyższym celu dokonano
pomiarów modułu piezoelektrycznego d na drodze wykorzystania obciążenia mechanicznego i
rejestracji powstałej na powierzchni materiału różnicy potencjałów (zjawisko piez. proste) oraz
pomiaru dylatometrem wydłużenia próbki podłączonej do wysokiego napięcia (zjaw. piez. odwrotne).
Ćwiczenie zawierało także część dotyczącą pomiaru stałej balistycznej galwanometru, co umożliwiło
zapoznanie się z metodą skalowania tego przyrządu.
Stałą balistyczną b obliczamy z następującej proporcji:
q=b⋅a ⇒ b=
q
a
[
C
dz
]
gdzie: q – ładunek, który przepłynął przez galwanometr [C], a – wychylenie wskazówki
galwanometru [dz]
Moduł piezoelektryczny d
33
dla zjawiska prostego można wyznaczyć ze wzoru:
q=d
33
F ⇒d
33
=
q
F
[
C
N
]
gdzie: Δq – przyrost ładunku [C], ΔF – odpowiadający mu przyrost obciążenia [N]
Zaś w zjawisku odwrotnym do obliczenia d
33
oraz d
31
posłużyły poniższe równości:
x=d
33
x
0
z
0
U
3
d
31
=
d
33
gdzie: U
3 –
napięcie przyłożone do płytki piezoelektryka [V], Δx – zmiana rozmiarów poprzecznych
płytki [m], x
0
, z
0
– wymiary nominalne płytki [m], γ – współczynnik Poissona
2. U
KŁADY
POMIAROWE
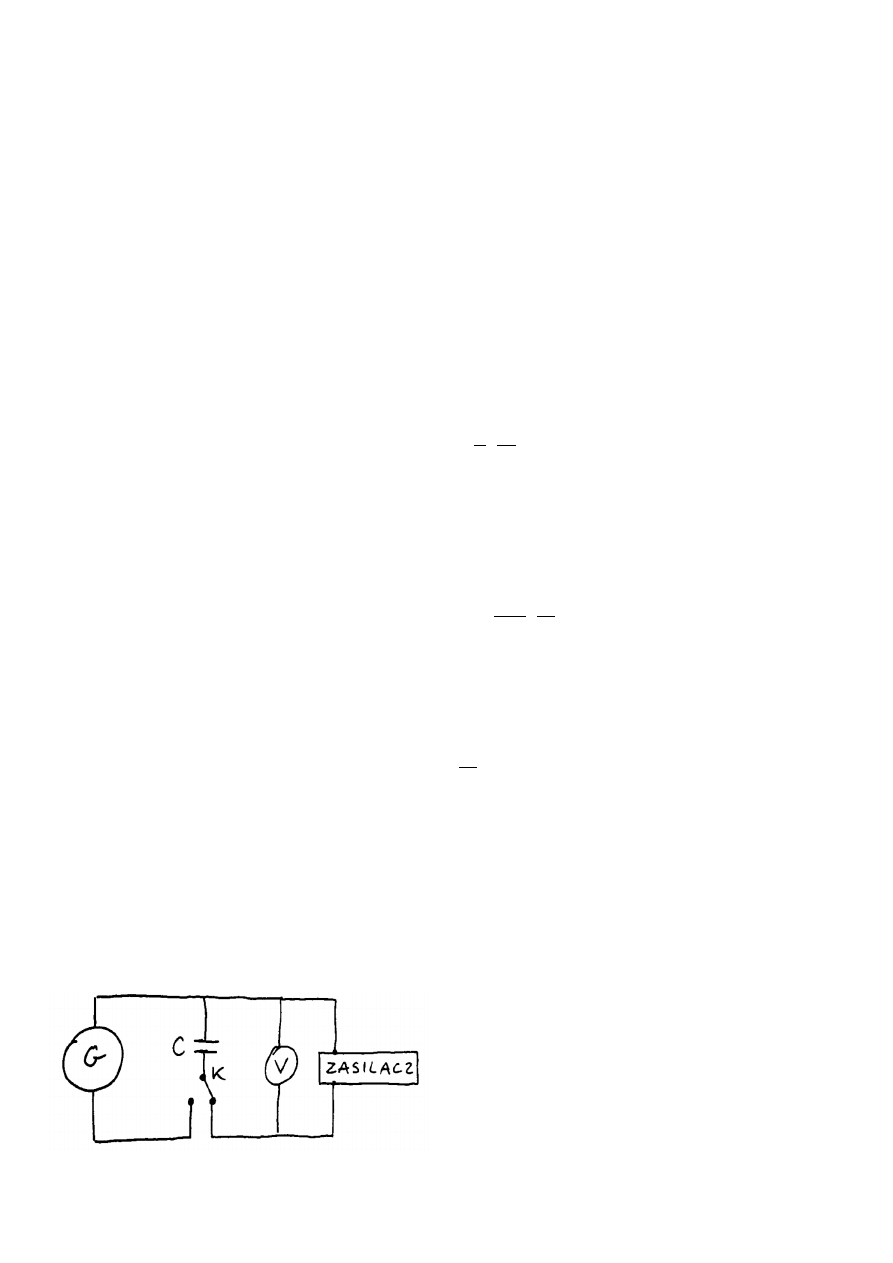
A. W
YZNACZANIE
STAŁEJ
BALISTYCZNEJ
Przepływ znanego ładunku przez galwanometr G
uzyskano rozładowując przezeń kondensator C o
określonej pojemności i zadawanym z zasilacza
(pracującego jako źródło napięciowe) napięciu
ładowania. Zmiana stanu pomiędzy „rozładowanie” i
„ładowanie” odbywała się poprzez zmianę położenia
klucza K. Pomiar napięcia ładowania odbywał się na
woltomierzu V włączonym równolegle w oczko
kondensator – zasilacz.
1
Rys. 1. Układ pomiarowy do podpunktu A
Parametry elementów układu:
- Galwanometr: klasa – 1,5; liczba działek – 140
- Kondensator: C = 5'000 pF
- Woltomierz: klasa – 1; liczba działek – 50; zakres – 10 V
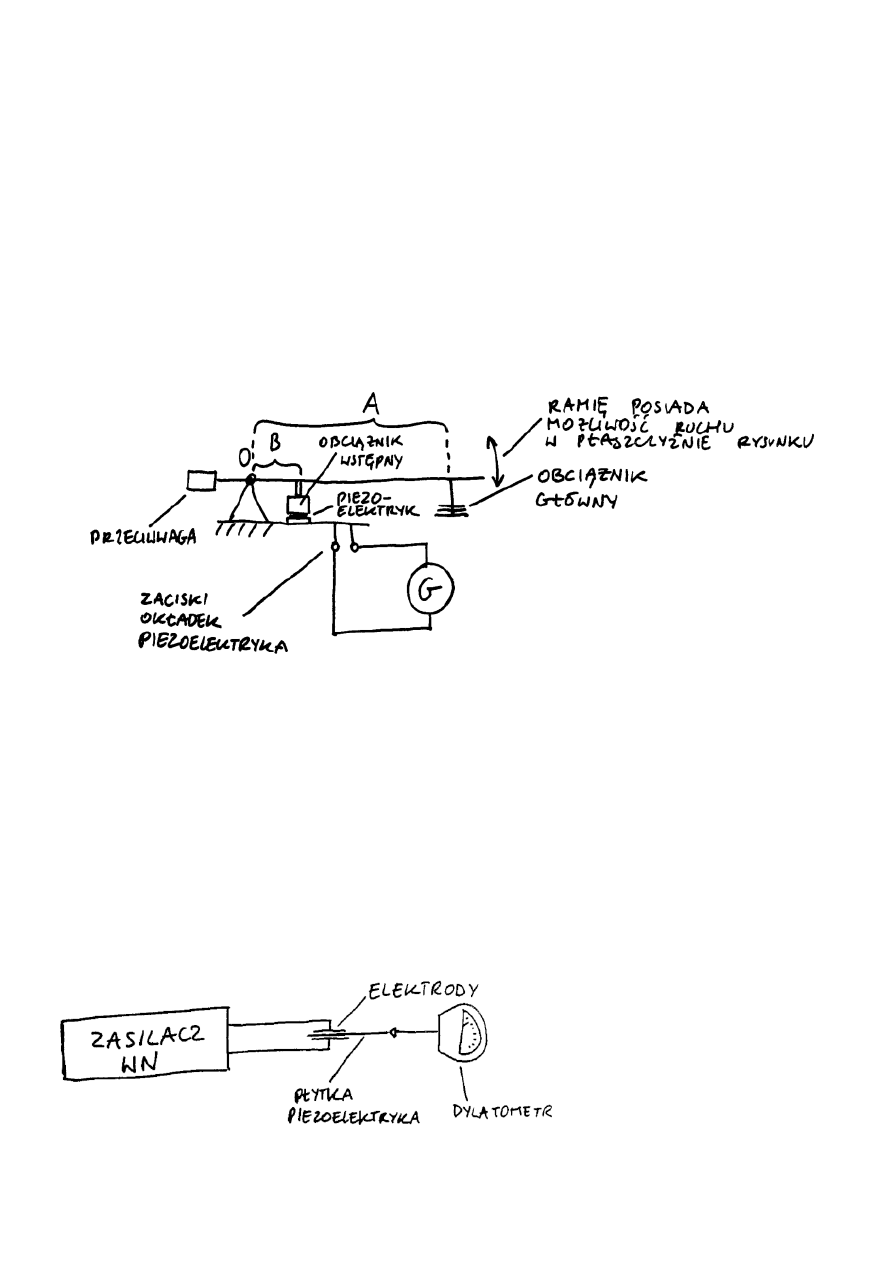
B. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
PROSTYM
Nacisk na element piezoelektryczny był uzyskiwany dzięki dźwigni posiadającej możliwość obrotu
wokół osi O. Modyfikowano obciążenie na ramieniu A, co zmieniało nacisk wywierany na
piezoelektryk przez dociskacz umocowany na ramieniu B. Ponieważ w stanie początkowym
dźwignia była wyważona, to zmienne obciążenie piezoelektryka pochodziło tylko od obciążnika
głównego. Ilość powstałego w wyniku zmiennego obciążenia ładunku polaryzacyjnego mierzono za
pomocą galwanometru wyskalowanego w części A ćwiczenia.
Parametry elementów układu:
- Galwanometr: klasa – 1,5; liczba działek – 140
- Dźwignia: długości ramion A i B – 1,10 i 0,10 m; obciążenie wstępne 4,22kg
pomiar długości ramion dźwigni: miarka o działce 1mm – stąd błąd systematyczny 0,5mm;
błąd ten wydaje się być jednak zaniżony, bowiem niemożliwe było utrzymanie przymiaru w
linii prostej i przyłożonego do dźwigni – dlatego błąd określam na 5mm dla ramienia A i
1mm dla ramienia B
- Obciążniki: masa - 0,500 ± 0,001 kg
C. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
ODWROTNYM
W układzie C wydłużenie próbki
materiału
piezoelektrycznego
uzyskiwano przez przyłączenie do
jej elektrod wysokiego napięcia
pochodzącego z nastawnego
zasilacza. Pomiar wydłużenia
elementu
odbywał
się
dylatometrem. Dylatometr oraz
piezoelektryk wraz z elektrodami
zamocowane były w ustalającym
ich wzajemne położenie korpusie.
2
Rys. 2. Układ pomiarowy do podpunktu B
Rys. 3. Układ pomiarowy do podpunktu C
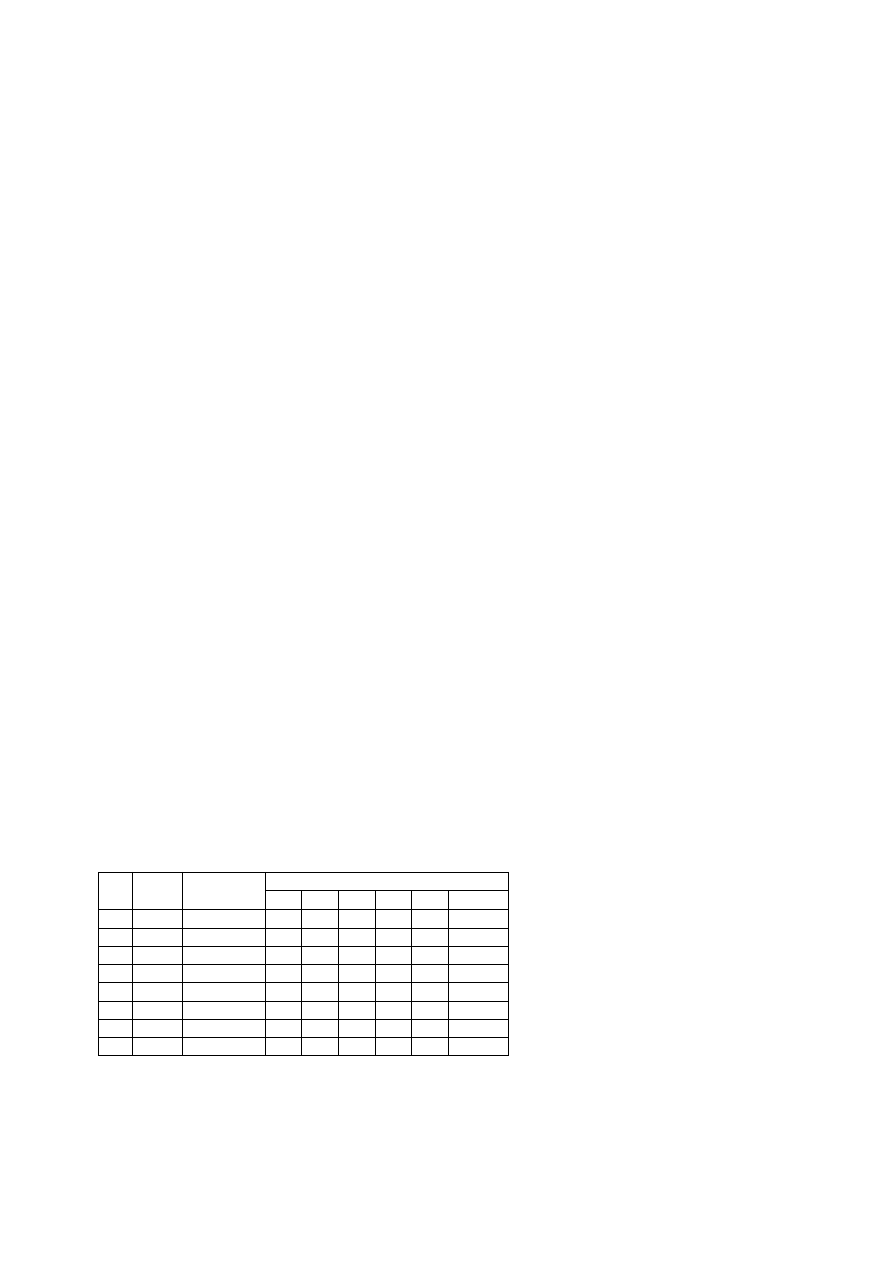
Parametry układu:
- Dylatometr: zakres – 60μm; l. działek – 60
- Zasilacz: działka – 0,01kV; zakres: 0 – 3,5kV
- Próbka piezoelektryka: wsp. Poissona γ=0,33; wymiary nominalne płytki: x
0
=110mm, z
0
=1,5mm
3. W
YKONANIE
ĆWICZENIA
A. W
YZNACZANIE
STAŁEJ
BALISTYCZNEJ
Po włączeniu układu do sieci i wyzerowaniu (po zdjęciu zwory) galawanometru wykonywano
następujący cykl pomiarowy:
1. Ustalenie napięcia na zasilaczu i odczyt jego wartości z woltomierza. Klucz zamyka gałąź
kondensator – zasilacz.
2. Pięciokrotne rozładowanie kondensatora poprzez chwilowe zamknięcie kluczem gałęzi
kondensator – galwanometr, któremu towarzyszyła obserwacja wskazań galwanometru.
Napięcia zadawane przez zasilacz zawierały się w przedziale 3÷6V i zmieniały ze skokiem 1V. Po
osiągnięciu wartości maksymalnej (6V) zmieniono polaryzację galwanometru i wykonywano te same
cykle pomiarowe, tym razem obserwując wychyły plamki w przeciwną stronę.
B. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
PROSTYM
Po wyzerowaniu galwanometru (po zdjęciu zwory) i sprawdzeniu wyważenia dźwigni wykonywano
cykliczne następujące czynności, aż do osiągnięcia obciążenia na obciążniku głównym równego 3kg:
1. Zwiększenie obciążenia na o jeden obciążnik pięćsetgramowy.
2. Opuszczenie dźwigni i obserwacja wskazania galwanometru.
3. Podniesienie dźwigni i obserwacja wskazania galwanometru.
C. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
ODWROTNYM
Po wyzerowaniu dylatometru wykonywano cykliczne poniższe czynności, aż do osiągnięcia
maksymalnego dopuszczalnego napięcia na zasilaczu 2,5kV.
1. Zwiększenie napięcia na zasilaczu o 0,5kV.
2. Odczyt wskazania dylatometru.
Następnie cykle zmieniły się i napięcie było zmniejszane do 0kV.
1. Zmniejszenie napięcia na zasilaczu o 0,5kV.
2. Odczyt wskazania dylatometru.
4. W
YNIKI
I
ICH
OPRACOWANIE
,
RACHUNEK
BŁĘDÓW
A. P
OMIAR
STAŁEJ
BALISTYCZNEJ
Tabela 1. Dane do obliczenia stałej balistycznej galwanometru.
Ładunek Q, który przepłynął przez galwanometr określono z następującego wzoru: Q=CU, ponieważ
C kondensatora była znana i wynosiła 5000pF.
3
lp
U [V]
Q [C]
a [działki * 10]
I
II
III
IV
V
średnia
1
3,0
1,50E-08 1,6
1,5 1,6 1,5
1,6
1,56
2
4,0
2,00E-08 2,1
2,1 2,1 2,1
2,0
2,08
3
5,0
2,50E-08 2,6
2,6 2,6 2,7
2,7
2,64
4
6,0
3,00E-08 3,2
3,1 3,1 3,2
3,2
3,16
5
-6,0
-3,00E-08 -3,1 -3,1 -3,2 -3,0 -3,1
-3,1
6
-5,0
-2,50E-08 -2,6 -2,6 -2,5 -2,6 -2,5
-2,56
7
-4,0
-2,00E-08 -2,1 -2,0 -2,0 -2,0 -2,0
-2,02
8
-3,0
-1,50E-08 -1,6 -1,5 -1,5 -1,5 -1,5
-1,52
Najlepszym przybliżeniem wartości wychylenia plamki galwanometru przy ustalonym ładunku na
kondensatorze jest średnia arytmetyczna z każdej serii 5 odczytów:
a
śr
=
1
5
∑
a
i
i tak przykładowo dla pomiaru 2: a
śr2
=
2,12,12,12,12,0
5
=
2,08[10⋅dz ]
odchylenie standardowe pojedynczego pomiaru:
s
d2
=
4 2,1−2,08
2
2,0−2,08
2
5−1
≈
4,472⋅10
−
2
[
10⋅dz ]
Błąd systematyczny pomiaru galwanometru określimy znając jego klasę 1,5 oraz zakres 140
(wyrażony w działkach):
a
s
=
1,5
100
⋅
140=2,1 [dz ]=0,21 [10⋅dz ]
Z teorii wiemy, że wzór na stałą balistyczną ma następującą postać:
b=
q
a
⇒
b=
CU
a
z powyższego dla pomiaru 2:
b=
5⋅10
−
9
[
F ]⋅4,0[V ]
2,08[10⋅dz ]
=
2,0⋅10
−
8
[
C ]
2,08[10⋅dz ]
≈
9,615⋅10
−
9
[
C
10⋅dz
]
Bład stystematyczny pomiaru napięcia wynosi:
U
s
=
0,1
1
100
⋅
10=0,2 [V ]
jest to suma błędu pochodzącego od odczytu (działka 0,2 V) oraz od klasy przyrządu (klasa 1,
zakres 10V).
Stąd błąd systematyczny stałej balistycznej:
b
s
=
∣
∂
b
∂
U
∣
U
s
∣
∂
b
∂
a
∣
a
s
=
C
a
śr2
U
s
CU
a
śr2
2
a
s
=
5⋅10
−
9
2,08
0,2
2,0⋅10
−
8
2,08
2
0,21≈1,452⋅10
−
9
[
C
10⋅dz
]
Błąd przypadkowy pojedynczego pomiaru, po uwzględnieniu współczynnika t-studenta dla poziomu
ufności 0,99 i liczby stopni swobody k=4 [t(0,99;4)=4,60]:
b
p1
=
s
b
⋅
t=
s
d2
∣
∂
b
∂
a
∣
2
t 0,99 ; 4=s
d2
CU
a
śr2
2
t 0,99 ;4=4,472⋅10
−
2
2⋅10
−
8
2,08
2
⋅
4,6≈9,510⋅10
−
10
[
C
10⋅dz
]
Ponieważ błąd przypadkowy jest porównywalny z systematycznym, oba należy uwzględnić w
obliczeniach.
Dla poziomu ufności bliskiemu 1:
b
1
=
b
p1
b
s
=
b
p1
5
b
s
≈
4,253⋅10
−
10
1,452⋅10
−
9
=
1,877⋅10
−
9
[
C
10⋅dz
]
≈
2⋅10
−
10
[
C
dz
]
Natomiast przy przenoszeniu wariancji (poziom ufności 0,682):
b
p2
=
1
5
s
d2
∣
∂
b
∂
a
∣
2
t 0,682 ;4=
1
5
s
d2
CU
a
śr2
2
t 0,682 ; 4=
=
2⋅10
−
2
2⋅10
−
8
2,08
2
⋅
1,15≈1,063⋅10
−
10
[
C
10⋅dz
]
b
2
=
b
p2
2
b
s
2
3
≈
1,1300⋅10
−
20
7,0277⋅10
−
19
≈
8,4500⋅10
−
10
[
C
10⋅dz
]
=
9⋅10
−
11
[
C
dz
]
b=10±2⋅10
−
10
[
C
dz
]
- wynik na poziomie ufności
≃
1
b=96±9⋅10
−
11
[
C
dz
]
- wynik na poziomie ufności ≃0,682
4
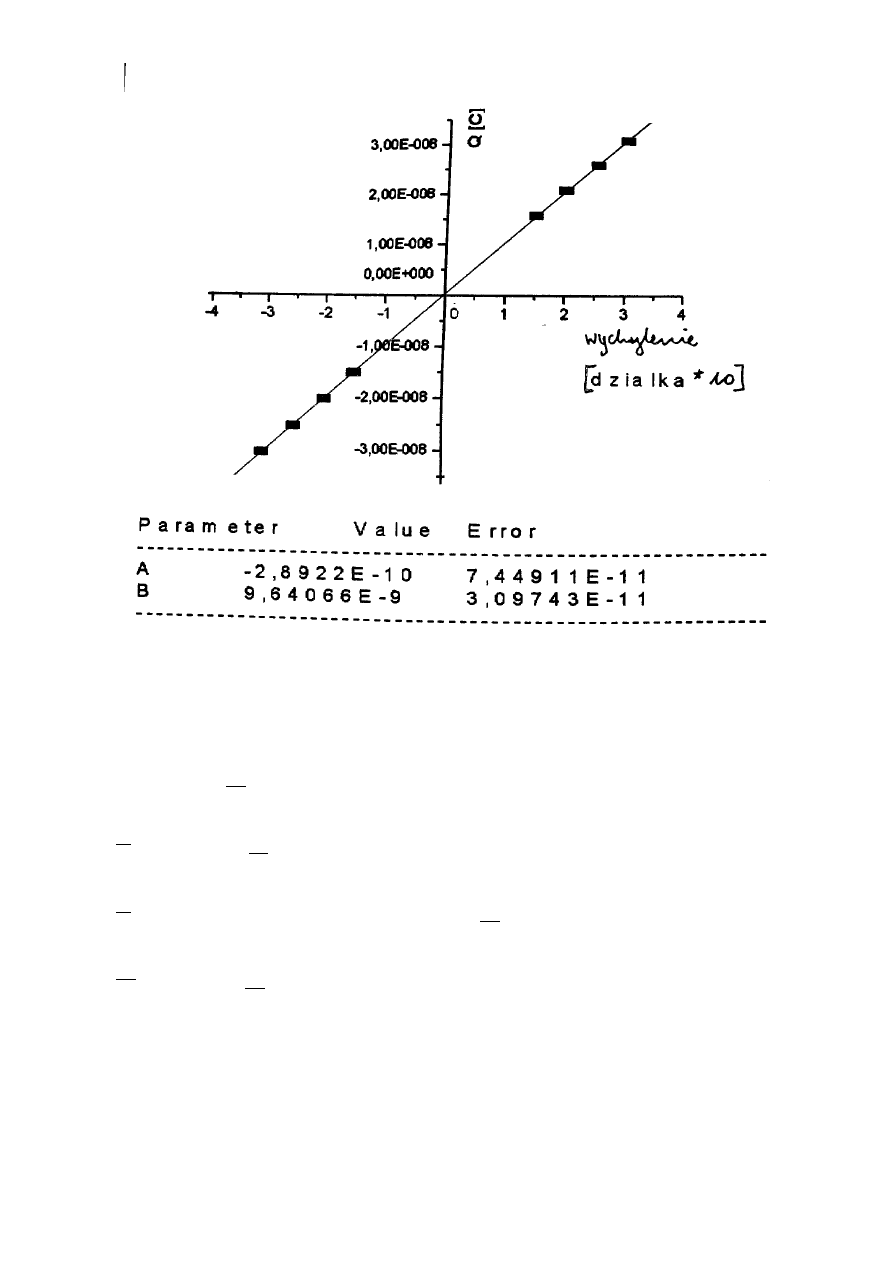
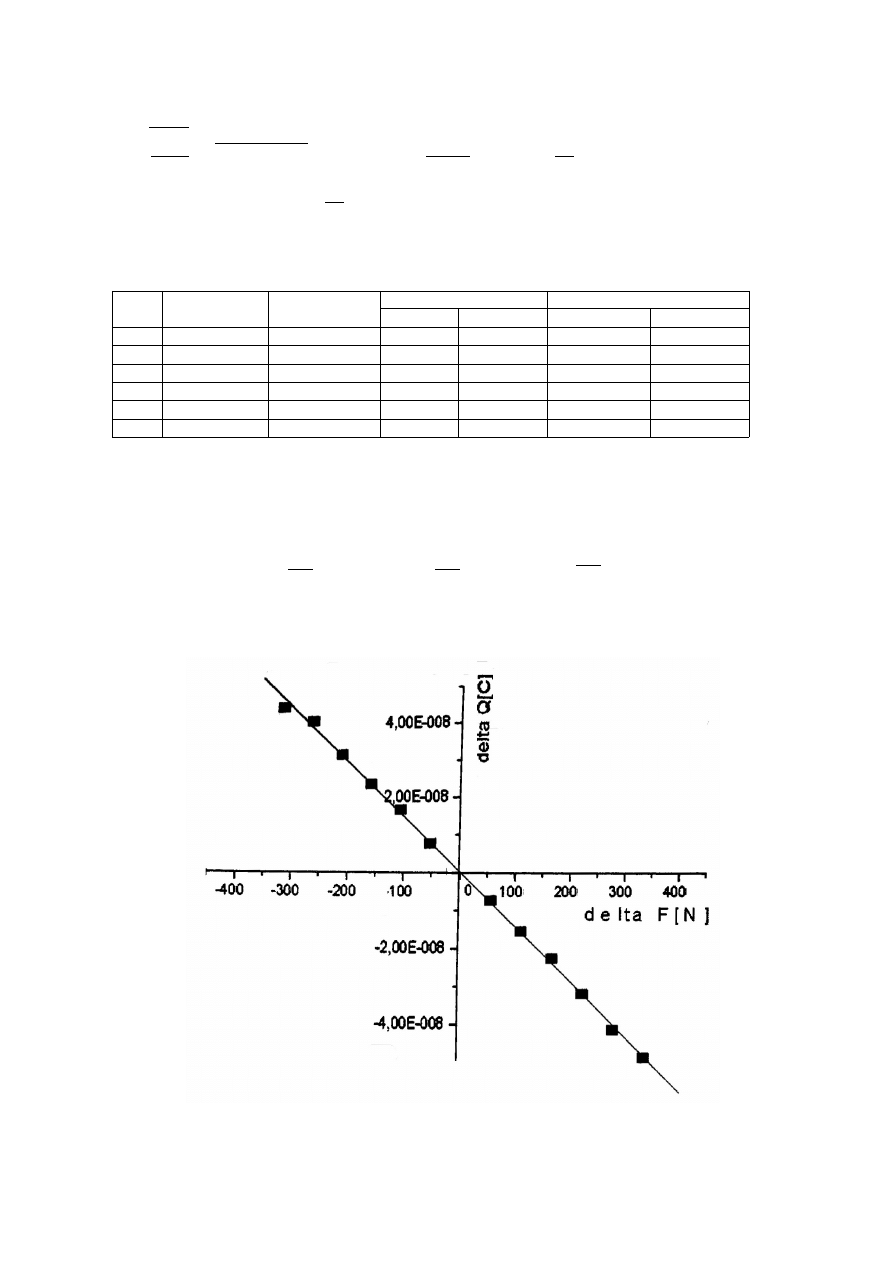
Wykres 1. Wykres z programu Origin przedstawiający aproksymację liniową zależności ładunku
przepływającego przez galwanometr od odczytanego wychylenia plamki.
Program Origin aproksymując wyniki linią prostą, obliczył stałą balistyczną (współczynnik
nachylenia prostej) równą:
b=9,6407⋅10
−
10
[
C
dz
]
zaś jej błąd przypadkowy:
b
p
=
3,0974⋅10
−
12
[
C
dz
]
co po uwzględnieniu współczynnika t-studenta dla 6 stopni swobody i
≃
0,682
b
p
⋅
t 0,682 ;6=3,0974⋅10
−
12
⋅
1,10=3,4071⋅10
−
12
[
C
dz
]
Jak widać błąd przypadkowy wynikły z zastosowania tej metody jest o wiele mniejszy niż
b
p1
=
4,253⋅10
−
10
[
C
dz
]
co ma swoje źródło w jej specyfice oraz w wykorzystaniu większej liczby
danych pomiarowych.
5
Jednak przyjmując wynik pochodzący z programu Origin należy rozważyć, czy brać pod uwagę błąd
systematyczny. Jako że jest on znacznie większy od błędu przypadkowego, okazuje się, że to właśnie
ten drugi możemy pominąć, w związku z czym dla poziomu ufności 0,682 mamy:
b=
b
s
2
3
≈
7,0277⋅10
−
19
≈
8,3831⋅10
−
10
[
C
10⋅dz
]
=
9⋅10
−
11
[
C
dz
]
i ostatecznie: b=96±9⋅10
−
11
[
C
dz
]
na poziomie ufności ≃0,682
B. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
PROSTYM
Tabela 2. Dane do obliczenia modułu piezoelektrycznego w zjawisku p. prostym.
Ładunek Q, który przepłynął przez galwanometr, określono z następującego wzoru: Q=ba, gdzie a -
wychylenie [dz], zaś b – stała balistyczna obliczona w pierwszej części ćwiczenia [C/dz]. Nacisk
obliczono korzystając z równania statyki uwzględniającego zerowanie się momentów dźwigni:
l
obc
F
obc
=
l
nac
F
nac
⇒
F
nac
=
l
obc
l
nac
F
obc
⇒
F
nac
=
mg
l
obc
l
nac
wiedząc, że
l
obc
l
nac
=
11
gdzie: m – obciążenie [kg]; l
obc
, l
nac
- długości ramienia obciążanego i naciskającego [m];
g - przyspieszenie ziemskie [m/s
2
]
Wykres 2. Zależność między zmianą obciążenia piezoelektryka a wywołanym nią przepływem
ładunku przez galwanometr dołączony do elektrod ww.
6
lp
obciążenie [kg] siła nacisku [N]
wychylenie [działka*10]
ładunek [C]
docisk
zdjęcie
docisk
zdjęcie
1
0,5
53,9
-0,8
0,7 -7,68000E-09 6,72000E-09
2
1
107,8
-1,6
1,6 -1,53600E-08 1,53600E-08
3
1,5
161,7
-2,3
2,3 -2,20800E-08 2,20800E-08
4
2
215,6
-3,2
3,1 -3,07200E-08 2,97600E-08
5
2,5
269,5
-4,1
4,0 -3,93600E-08 3,84000E-08
6
3
323,4
-4,8
4,4 -4,60800E-08 4,22400E-08
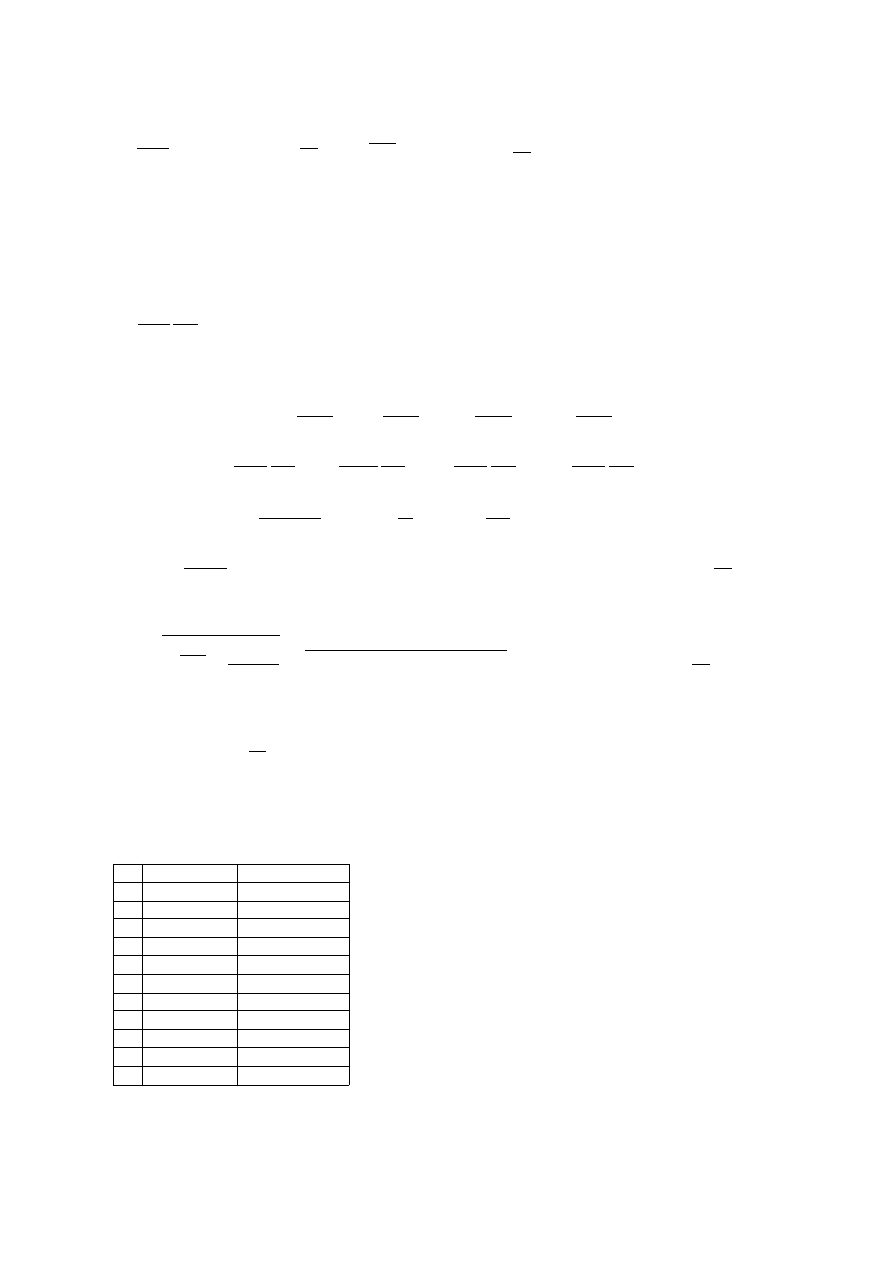
Dla danych z Tablicy 2 program Excel obliczył współczynnik nachylenia prostej regresji
odpowiadający szukanemu modułowi d
33
, a także jego błąd przypadkowy Δd
33 p
:
d
33
=
q
F
=−
1,3955⋅10
−
10
[
C
N
]
d
33p
=
1,4445⋅10
−
12
[
C
N
]
ponieważ liczba pomiarów przewyższa 10, nie ma potrzeby wymnażania błędu przypadkowego przez
współczynnik t-studenta.
Wartość d
33
należy skorygować zapisując moduł jako dodatni, ponieważ kierunek przepływu ładunku,
a tym samym znak przyrostu Δq, zależy tylko od sposobu zestawienia układu pomiarowego.
Aby obliczyć błąd systematyczny przekształcono wzór na moduł piezoelektryczny tak, aby był on
jawną funkcją mierzonych wartości:
d
33
=
q
m⋅g
l
nac
l
obc
stąd można policzyć, obierając przykładowy punkt o obciążeniu 2kg, w chwili docisku
(ładunek: -3,072e-8):
d
33s
=
∣
∂
d
33
∂
q
∣
q
∣
∂
d
33
∂
m
∣
m
∣
∂
d
33
∂
l
obc
∣
l
obc
∣
∂
d
33
∂
l
nac
∣
l
nac
=
=
1
m⋅g
l
nac
l
obc
q
q
m
2
⋅
g
l
nac
l
obc
m
q
m⋅g
l
nac
l
obc
2
l
obc
q
m⋅g
1
l
obc
l
nac
=
=
1
m⋅g⋅l
obc
l
nac
q
q
m
l
nac
m
q
l
obc
l
nac
l
obc
q l
nac
=
=
1
21,56
9⋅10
−
12
1,536⋅10
−
12
1,3964⋅10
−
11
3,072⋅10
−
11
=
2,5612⋅10
−
12
[
C
N
]
ponieważ błąd systematyczny jest podobnego rzędu co przypadkowy, wypadkowy błąd obliczam z
metody przenoszenia wariancji:
d
33
=
d
33p
2
d
33s
2
3
≈
2,0866⋅10
−
24
6,5597⋅10
−
24
≈
2,9406⋅10
−
12
=
3⋅10
−
12
[
C
N
]
Ostateczny zapis wyniku:
d
33
=
140±3 10
−
12
[
C
N
]
C. W
YZNACZANIE
MODUŁU
PIEZOELEKTRYCZNEGO
W
ZJAWISKU
P
.
ODWROTNYM
Tabela 3. Dane do obliczenia modułu piezoelektrycznego w zjawisku p. odwrotnym.
7
lp
napięcie [kV] wydłużenie [um]
1
0
0
2
0,5
-3
3
1
-6,5
4
1,5
-10,2
5
2
-14,5
6
2,5
-20
7
2
-17
8
1,5
-15
9
1
-10,5
10
0,5
-6
11
0
-1
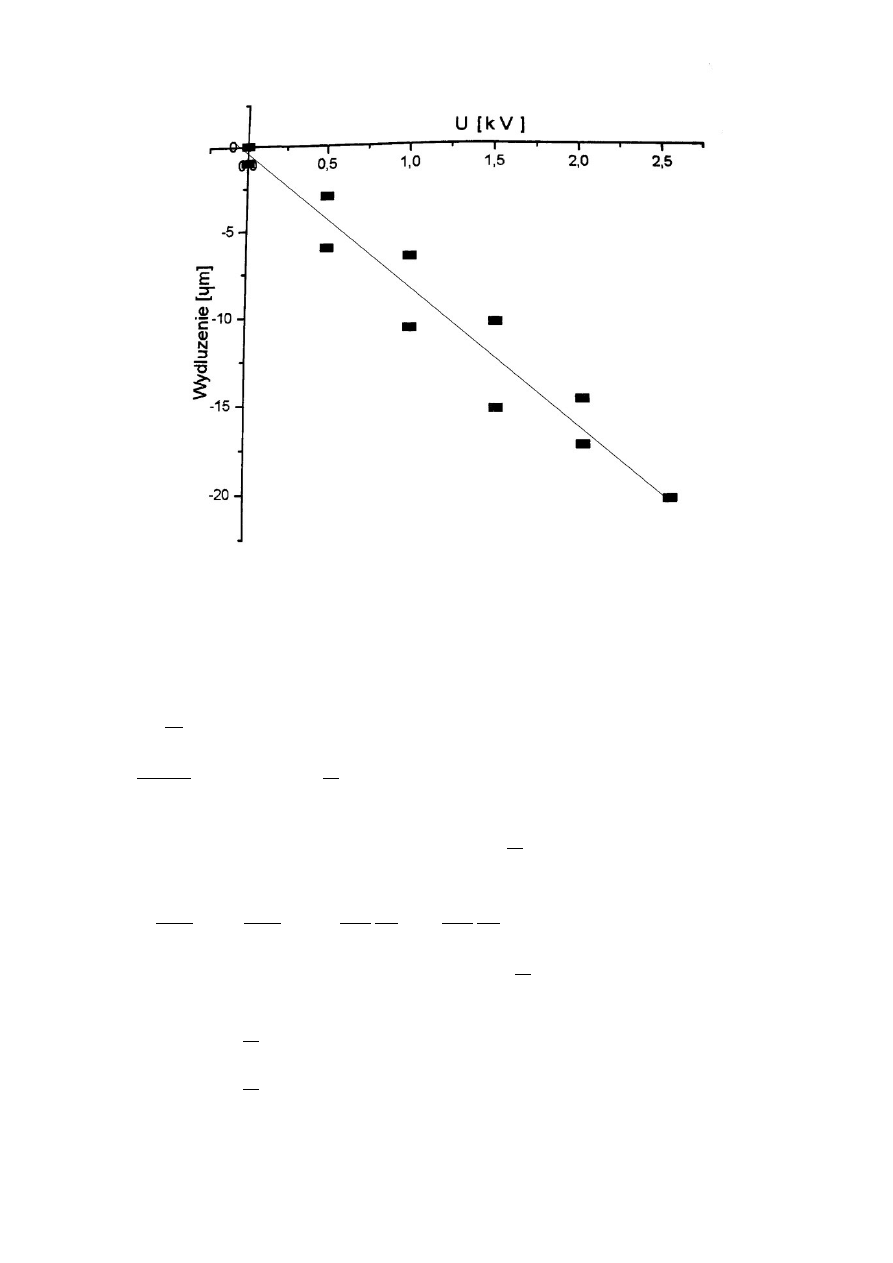
Wykres 3. Zależność między wydłużeniem poprzecznym Δx piezoelektryka a zmianą napięcia do
niego przyłożonego. Widoczna jest histereza materiału i pewna pozostałość odkształcenia. Odcinek
oznacza wielką półoś quasi elipsy.
Moduł d
33
obliczam w punkcie (2500,-20) korzystając ze wzoru:
x=d
33
x
0
z
0
U
3
d
33
=
z
0
x
x
0
U
3
≈−
3,2058⋅10
−
10
[
m
V
]
Moduł d
31
natomiast:
d
31
=
d
33
⇒
d
31
=−
0,33∗3,2058⋅10
−
10
≈−
1,0579⋅10
−
10
[
m
V
]
Błąd systematyczny (dylatometr: 0,5μm; woltomierz: 10V – błędy odczytu):
d
33
=
∣
∂
d
33
∂
x
∣
x
∣
∂
d
33
∂
U
3
∣
U
3
=
z
0
x
0
1
U
3
x
z
0
x
0
x
U
3
2
U
3
≈
≈
8,2645⋅10
−
12
1,3223⋅10
−
12
=
9,5868⋅10
−
12
=
1⋅10
−
11
[
m
V
]
Ostateczny zapis (znak modułu pominięty jako pochodzący tylko od zestawienia układu):
d
33
=
32±1⋅10
−
11
[
m
V
]
d
31
=
11±1⋅10
−
11
[
m
V
]
dla poziomu ufności ≃1
8
5. W
NIOSKI
Piezoelektryki charakteryzują się w badanym zakresie dobrą liniową zależnością wytwarzanego
ładunku od nałożonego obciążenia. Wyraźnie zaobserwować można także histerezę i pozostałości
odkształceniowe w próbkach podczas badania zjawiska piezoelektrycznego odwrotnego. Wszystkie
pomiary charakteryzowały się zadowalającymi dokładnościami, tzn. ich błędy względne nie
przekraczały 10%. Można stwierdzić, że urządzenia pomiarowe są dobrane optymalnie do charakteru
pomiarów – błędy systematyczne i przypadkowe pozostają zbliżone do siebie.
9