Przebieg laboratorium

1. Zestawienie obwodu i ustawienie rezystancji R₁ tak aby zrównoważenie mostka następowało przy położeniu suwaka w zakresie 200-300 działek na skali helipotu.

2. Wykonanie około 250 pomiarów oporu R_x.

Tabela wyników:

Wskazania helipotu	Liczba powtórzeń
247	2
248	18
249	50
250	82
251	68
252	30
253	10

3. Obliczanie wartości średniej położenia suwaka helipotu dwoma sposobami:

a). = 250,25 dz.

b). = 250,25 dz.

4. Obliczanie odchylenia standardowego σ pojedynczego pomiaru:

= 1,25 dz.

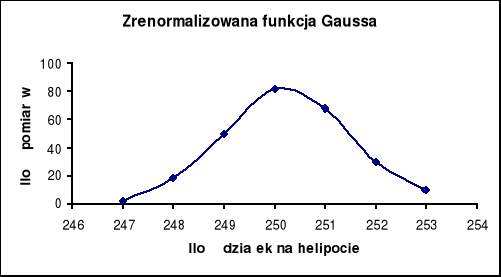
5. Zrenormalizowanie funkcji Gaussa podstawiając za stałą C we wzorze

pole powierzchni histogramu (liczbę pomiarów).

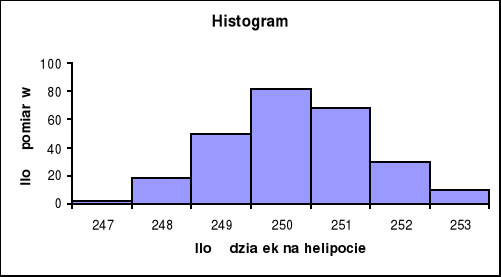
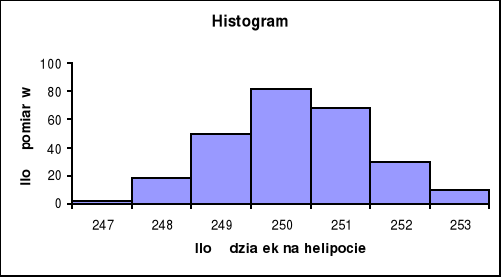
6. Narysowanie histogramu w postaci kolumn oraz zrenormalizowanej funkcji Gaussa:

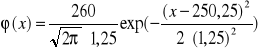
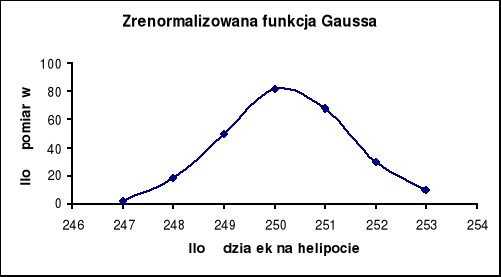
7. Obliczenie wartości procentowej wyników pomiarów w przedziałach:

(-σ  σ)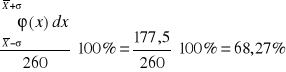

(-2σ ; 2σ)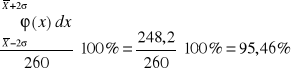

(-3σ ; 3σ)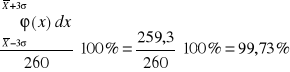

Po odczytaniu z wykresu otrzymujemy dla:

(-σ ; σ)
= 76,2%

(-2σ ; 2σ)
= 95,38%

(-3σ ; 3σ)
= 100%

Powyższe wartości są bardzo bliskie wynikom teoretycznym co oznacza, że ćwiczenie oraz obliczenia były przeprowadzone poprawnie.

9. Obliczenie wartości oporu R_x

R_x =
= 183,6 Ω

Błąd bezwzględny średni:

R_x = = 1,22 Ω, gdzie n_x = σ

Błąd bezwzględny maksymalny:

R_x = = 3,67 Ω, gdzie n_x = 3σ.

Błąd względny procentowy:

średni δR_x = = 0,49 %

maksymalny δR_x == 1,47 %

Wnioski:

Duży wpływ na błędy pomiarowe miała dokładność helipotu, między innymi brak idealnej liniowości przesuwu suwaka helipotu. Błąd wnoszony przez dekadę wzorcową jest tutaj mało istotny w porównaniu z innymi błędami. Natomiast ważną zaletą pomiaru rezystancji mostkiem Wheatstone'a jest brak wpływu wahań napięcia zasilającego na wynik pomiaru.

Pole pod znormalizowaną krzywą Gaussa wyraża prawdopodobieństwo tego, że zmienna losowa przejmie wartości zawarte w tym polu. Zrenormalizowana funkcja Gaussa wyraża nam już nie czyste prawdopodobieństwo lecz liczbę pomiarów przyjmujących wartości oczekiwane.

---