EAIiE	Imię i nazwisko: 1. Krzysztof Jasek 2. Piotr Jóźwik			Rok: I	Grupa: III	Zespół: 12
Pracownia Fizyczna	Temat: Współczynnik lepkości							Nr ćwiczenia: 13
Data wykonania: 23.02.2001	Data oddania: 2.03.2001	Zwrot do poprawy:	Data oddania:	Data zaliczenia:	Ocena:

Cel ćwiczenia:

Zapoznanie się z własnościami cieczy lepkiej, wyznaczanie współczynnika lepkości metodą spadania kulki (metodą Stokesa).

Wprowadzenie:

Przy przepływie wszystkich cieczy rzeczywistych ujawniają się siły tarcia występujące w całej objętości - tzw. tarcie wewnętrzne lub lepkość.

Rozważmy układ dwóch płaskich płytek o powierzchni S oddalonych od siebie o d wraz z wypełniającą dokładnie objętość cieczą zawartą między nimi. W przypadku, gdy jedna z płytek porusza się z niewielką prędkością v, siła F potrzebna do podtrzymania ruchu jest proporcjonalna do powierzchni S i prędkości v a odwrotnie proporcjonalna do odległości d:

gdzie stałą η nazywamy współczynnikiem lepkości.

Zjawisko lepkości występuje we wszystkich cieczach i gazach, wykazując zależność od temperatury (wraz ze wzrostem temperatury: - dla cieczy zmniejsza się znacznie, - dla gazów rośnie proporcjonalnie). Lepkość jest odpowiedzialna za występowanie oporów ruchu. Na ciało poruszające się w płynie z prędkością v działa siła oporu ruchu, która zależy od prędkości, gęstości płynu, wielkości l poruszającego się ciała wyrażonej przez jego wymiar liniowy w kierunku prostopadłym do wektora prędkości oraz właśnie współczynnika lepkości. Z wymienionymi wielkościami wiąże się tzw. liczba Reynoldsa:

Od wartości tej liczby zależy charakter ruchu płynu (laminarny lub turbulentny). Jeżeli liczba Reynoldsa jest dużo mniejsza od jedności (Re<<1), siłę oporu ruchu działającą na poruszającą się w cieczy kulkę wyraża wzór:

gdzie:

v - prędkość kulki

r - promień kulki

Wzór ten jest słuszny gdy zakładamy nieograniczoną objętość cieczy. Jeżeli ruch odbywa się wzdłuż osi cylindra z cieczą o promieniu R to wzór na siłę F ma postać:

Na spadającą w cieczy kulkę działają trzy siły:

F = mg - siła ciężkości

F_w = m_wg = ρVg - siła wyporu Archimedesa, gdzie:

ρ - gęstość cieczy

V - objętość kulki

F_o = Kv - siła oporu ruchu (siła Stokesa), gdzie:

Równanie ruchu kulki ma więc postać:

czyli:

Rozwiązując równanie różniczkowe dla chwili początkowej t₀=0 i prędkości v₀ otrzymujemy:

gdzie nazywamy stałą czasową.

Ponieważ drugi wyraz po prawej stronie wzoru maleje eksponencjalnie z czasem, więc po czasie rzędu 3 stanie się zaniedbywalnie mały a kulka poruszać się będzie z prędkością graniczną:

stąd otrzymujemy:

Doświadczenie polegać więc będzie na pomiarze wszystkich wielkości występujących po prawej stronie powyższego równania.

Aparatura:

Pionowy cylinder wypełniony gliceryną ma średnicę D=2R. Na cylindrze umieszcza się poziome paski w odległości l jeden od drugiego. Górny pasek jest co najmniej 3τv poniżej powierzchni gliceryny - tak by kulka od górnego paska poruszała się już ze stała prędkością, którą zmierzymy wyznaczając czas poruszania się kulki pomiędzy paskami. Masy m kulek zostaną wyznaczone za pomocą wagi elektronicznej, a ich średnica d określona przy pomocy śruby mikrometrycznej.

Obliczenia:

T=19°C - temperatura otoczenia podczas wykonywania ćwiczenia

l=800 mm - długość drogi przebytej przez kulki w glicerynie

D=34 mm - średnica wewnętrzna cylindra

ρ=1,28 g/cm³ - gęstość gliceryny

Pomiar czasu t spadania po drodze l wykonaliśmy stoperem po trzy razy dla każdej z dziesięciu kulek. Wyniki pomiarów zostały zebrane w tabeli. Do obliczenia prędkości poszczególnych kulek posłużyliśmy się średnią czasu spadania t_śr. Prędkość v_gr wyznaczamy ze wzoru na prędkość w ruchu jednostajnym prostoliniowym. Przyjmujemy, że kulki po przebyciu pewnej, nie branej przez nas pod uwagę drogi w glicerynie, poruszają się dalej takim właśnie ruchem.

Lepkość gliceryny  obliczyliśmy znając już wszystkie potrzebne wielkości, zmierzone lub wyznaczone.

tabela wyników:

	m	d	t1 t2 t3	tśr	vgr		
LP	[mg]	[mm]	[s]	[s]	[m/s]	[Pa*s]
			6,60
1	262	4,01	6,62	6,59	0,121	0,365	0,005
			6,56
			6,63
2	256	3,96	6,62	6,61	0,121	0,364	0,005
			6,58
			6,53
3	254	3,96	6,54	6,55	0,122	0,357	0,005
			6,59
			6,50
4	261	4,00	6,55	6,53	0,123	0,361	0,005
			6,54
			6,69
5	263	4,01	6,71	6,72	0,119	0,373	0,005
			6,75
			6,97
6	255	3,97	6,96	6,95	0,115	0,379	0,005
			6,93
			7,03
7	252	3,96	6,99	6,98	0,115	0,377	0,006
			6,91
			10,16
8	131	3,19	10,16	10,12	0,079	0,368	0,009
			10,03
			6,84
9	265	4,01	6,81	6,81	0,117	0,382	0,005
			6,78
			6,91
10	255	3,97	6,81	6,84	0,117	0,373	0,005
			6,81
						0,370	0,005

Szacowanie błędów:

Δm=±2 mg - błąd pomiaru masy kulek.

Δd=±0,01 mm - błąd pomiaru średnicy kulek.

Δl=±1mm - błąd pomiaru długości drogi spadania kulek.

Pomiary wykonywane przez nas przy tym ćwiczeniu obarczone były błędami zarówno przypadkowymi jak i systematycznymi. Błędy systematyczne to błędy pomiaru masy, średnicy kulek oraz długości drogi jednostajnego spadania kulek. Błędem przypadkowym został obarczony pomiar czasu spadania kulki. Wynika on z czasu reakcji prowadzącego pomiary na bodźce wzrokowe.

Przy obliczaniu błędu pomiaru lepkości gliceryny, korzystamy z prawa przenoszenia błędów. Zgodnie z zaleceniami pomijamy czynnik poprawkowy postaci (1+2,4⋅r/R). Eliminujemy także ze wzoru, zmienną V (objętość kulki), przez podstawienie odpowiedniej zależności:

; ;

;

Błąd pomiaru prędkości spadania kulki w glicerynie obliczamy z prawa przenoszenia błędów:

.

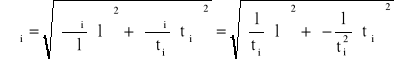
Jest on spowodowany zarówno błędem systematycznym (pomiar długości drogi), jak i błędem przypadkowym (pomiar czasu ruchu kulek). Całkowity błąd pomiaru czasu możemy wyznaczyć obliczając odchylenie standardowe średniej pomiarów, korzystając z zależności:

.

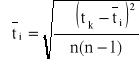
W naszym przypadku n=3 (ilość pomiarów dla każdej kulki),więc średnia czasu spadania pojedynczej kulki wynosi:

.

Znając­ Δν_i możemy obliczyć przyczynki do błędu pomiaru lepkości.

przyczynek błędu wynikający z pomiaru masy kulek

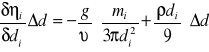
przyczynek spowodowany pomiarem średnicy

przyczynek wynikający z pomiaru prędkości

Następnie obliczamy błędy pomiaru lepkości gliceryny z prawa przenoszenia błędów:

, czyli:

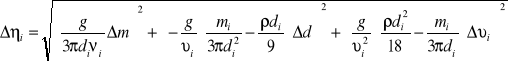
Wyniki obliczeń lepkości i jej odchyłek dla poszczególnych kulek zostały umieszczone w tabeli.

Wnioski:

W wyniku przeprowadzonego doświadczenia uzyskaliśmy wartość lepkości badanej cieczy przy temperaturze 19⁰C równą 0,370 Pa*s obarczoną błędem =0,005.

W związku z bardzo silną zmianą lepkości gliceryny przy nawet bardzo niewielkiej domieszce wody, i nieznanej zawartości wody w badanej glicerynie pominięto obliczenie błędu tablicowego, gdyż nie byłby on adekwatny do rzeczywistości. Na podstawie otrzymanego wyniku można jednak oszacować zawartość wody w glicerynie na ok. 7-10%, przy tej wartości bowiem tabelaryczna lepkość gliceryny jest najbliższa otrzymanemu wynikowi. Ponadto przyczynek do błędu wnosił czas ruchu kulki wewnątrz cylindra. Gdy kulka nie poruszała się centralnie wewnątrz cylindra, jej czas opadania był krótszy. Niewielki wpływ na błąd miała dokładność pomiaru masy i promienia (przyrządy były bardzo dokładne: waga elektroniczna i śruba mikrometryczna).

---