Sprawozdanie z ćwiczeń
w laboratorium wytrzymałości materiałów

Badanie odporności na pękanie w płaskim stanie odkształcenia

1. Wiadomości wstępne .

W obliczeniach przyjmuje się, że konstrukcja jest wystarczająco wytrzymała, jeśli naprężenie w niej wyst jest mniejsze od dopuszczalnego.Według hipotezy Griffitha szczelina o długości 2l w sprężyście i równomiernie rozciąganej płytce o nieskończenie wielkich wymiarach i o jednostkowej grubości powoduje obciążenie obszaru wokół szczeliny . Przy jednostkowej energii odkształcenia sprężystego , odciążenie obszaru płyty o polu S powoduje zmniejszenie się energii odkształcenia sprężystego . Wzrasta natomiast jednostkowa energia powierzchniowa konieczna do utworzenia nowej swobodnej powierzchni. Energia ta wynosi : 4l . Suma obu energii jest całkowitą energią rozwoju pęknięcia .

Po osiągnięciu maksimum tej energii dalszy rozwój pęknięcia określa energia potencjalna odkształcenia sprężystego płyty .

Rozwój pęknięcia następuje wówczas , gdy wartość osiąga wartość krytyczną .

Powyższe oznaczenie nosi nazwę współczynnika intensywności naprężeń .

Współczynnik K osiągający wartość krytyczną w chwili nieustannego , samoistnego wzrostu pęknięć oznacza się
i nazywa wytrzymałością na pęknięcie lub odpornością na rozwój pęknięcia i jest charakterystyczną wielkością materiałową . Powszechnie używa się zapisu
, co oznacza odporność na pękanie w płaskim stanie odkształcenia w najczęściej spotykanym przypadku obciążenia , do którego odnosi się wskaźnik I .

2. Cel ćwiczenia

Celem ćwiczenia jest :

a) zaznajomienie się z normą PN-87/H-04335

b) Zapoznanie się z metodą badania odporności materiału na pękanie w zakresie sprężystym

c) Wyznaczenie krytycznego współczynnika intensywności naprężenia

3. Przeprowadzenie próby K_Ic

Przygotowną próbkę do badań zakłada się do maszyny wytrzymałościowej. Obciążenie próbki może odbywać się przy stałej prędkości: narastanie obciążenia, rowarcia brzegów szczeliny lub zmiany intensywności naprężenia, w zależności od sposobu sterowania maszyną. Prróbkę należy tak obciążać, aby prędkości wzrostu intensywności natężenia mieści ła się w przedziale (0.55-2.75)[Mpa m^0.5 s^-0.5].

Podczas obciążenia rejestruje się zmianę siły w funkcji przemieszczenia brzegów szczeliny. Początkowe nachylenie liniowej części wykresu powinno być tak dobrane, aby można było dokładnie określić siłę krytyczną P_Q. Aby określić K_Ic należy wstępnie wyznaczyć warunkową wielkość na podstawie danych otrzymanych z krzywej rozciągania. Krzywa ta w układzie siła-rozwarcie brzegów szczeliny umośliwia wyznaczenie siły krytycznej P_Q. Należy w tym celu narysować sieczną OP₅ o nachyleniu (P/V)₅ =0.95( P/V)₀ , gdzie (P/V)₀ jest tangęsem kąta nachylenia prostej OA do początkowj prostoliniowej części wykresu. Jeżeli krzywa rozciągania nie posiada ekstremum, to wartość siły odpowiadająca temu punktowi jest równa P_Q Jeżeli przed punktem przecięcia się krzywych występuje max to za siłe krytyczną P_Q przyjmuje się P_max . po wyznaczeniu siły P_Q mależy obliczyć stosunek P_max /P_Q

Jeżeli stosunek ten jest większy od 1,10 to próbę unieważnia się. Jeżeli natomiast jest mniejszy, to obliczeniową wartość odporności na pękanie K_Q wyznacza się z wzoru

(1.1)

w którym :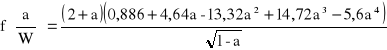
(1.2)

gdzie :
(1.3)

6. Tabela pomiarowa i obliczenia

L.p	U [mm]	F[daN]	F-50
1	0	55	5
2	0	60	10
3	0	65	15
4	0,01	85	35
5	0,02	100	50
6	0,03	110	60
7	0,04	120	70
8	0,05	135	85
9	0,06	145	95
10	0,07	155	105
11	0,08	160	110
12	0,09	170	120
13	0,1	180	130
14	0,11	190	140
15	0,12	195	145
16	0,13	205	155
17	0,14	210	160
18	0,15	220	170
19	0,16	225	175
20	0,17	230	180
21	0,18	240	190
22	0,19	245	195
23	0,2	255	205
24	0,21	260	210
25	0,22	265	215
26	0,23	280	230
27	0,24	285	235
28	0,25	295	245
29	0,26	300	250
30	0,27	310	260
31	0,28	315	265
32	0,29	320	270
33	0,3	325	275
34	0,31	330	280
35	0,32	340	290
36	0,33	350	300
37	0,34	360	310
38	0,35	370	320
39	0,36	375	325
40	0,37	380	330
41	0,38	385	335
42	0,39	390	340
43	0,4	395	345
44	0,41	400	350
45	0,42	400	350
46	0,43	400	350
47	0,44	400	350
48	0,45	400	350
49	0,46	405	355
50	0,47	405	355
51	0,48	405	355
52	0,49	405	355
53	0,53	385	335
54	0,54	395	345
55	0,55	400	350
56	0,56	400	350
57	0,57	400	350
58	0,58	395	345
59	0,59	385	335
60	0,6	375	325
61	0,61	360	310
62	0,62	360	310
63	0,63	340	290
64	0,64	330	280
65	0,66	310	260
66	0,67	310	260
67	0,68	300	250
68	0,7	280	230
69	0,71	275	225
70	0,72	270	220
71	0,73	260	210
72	0,74	255	205
73	0,75	245	195
74	0,76	240	190
75	0,77	240	190

Materiał próbki ZL250

Skala B na maszynie wytrzymałościowej KM-50-1

Długość pęknięcia zmęczeniowego as=0 mm

Próba przeprowadzona na bazie współczynnika intensywności naprężeń
- próba siłowa

W = 50,45 mm

B = 15,1mm

a = 29,9 mm

Obliczanie wzoru prostej stycznej do początkowego fragmentu wykresu zależności P i f

Korzystając z metody najmniejszych kwadratów otrzymujemy układ równań :

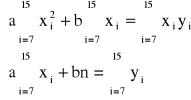
(2.1)

L.p	x	y	xy	x^2
1	0,08	110	8,8	0,0064
2	0,09	120	10,8	0,0081
3	0,1	130	13	0,01
4	0,11	140	15,4	0,0121
5	0,12	145	17,4	0,0144
6	0,13	155	20,15	0,0169
7	0,14	160	22,4	0,0196
8	0,15	170	25,5	0,0225
9	0,16	175	28	0,0256
10	0,17	180	30,6	0,0289
11	0,18	190	34,2	0,0324
12	0,19	195	37,05	0,0361
13	0,2	205	41	0,04
14	0,21	210	44,1	0,0441
15	0,22	215	47,3	0,0484
16	0,23	230	52,9	0,0529
17	0,24	235	56,4	0,0576
18	0,25	245	61,25	0,0625
19	0,26	250	65	0,0676
20	0,27	260	70,2	0,0729
21	0,28	265	74,2	0,0784
22	0,29	270	78,3	0,0841
23	0,3	275	82,5	0,09
24	0,31	280	86,8	0,0961
25	0,32	290	92,8	0,1024
26	0,33	300	99	0,1089
27	0,34	310	105,4	0,1156
suma	5,67	5710	1320,45	1,3545

Korzystając z powyższej tabeli i rozwiązując układ równań 2.1 otrzymujemy :

a = 740,84249 [daN]

b = 55,904558 [daN]

Wobec tego równanie stycznej I :

y = a*x + b

y = 740,84249*x + 55,904558

Równanie prostej II o współczynniku przy x o wartości 95% współcz. a stycznej I :

y = 0,95*a*x + b

y = 703,8004*x +55,904558

Siła odczytana z wykresu :

= 345 daN

Korzystając ze wzorów 1.1 , 1.2 , 1.3 otrzymujemy :

= 5,486

= 126416,6

Przyjmujemy

Warunek jest spełniony.

7. Wnioski.

Próba
pozwala na określenie odporności na rozwój pękania dla danego materiału. Badany materiał żeliwo ZL250, ze względu na swą kruchość uległ zniszczeniu. Na wykresie przyrostu wydłużenia w zależności od siły wyrażnie występowało maksimum. W czasie przeprowadzenia próby wystąpił poślizg szczęk dla kilkunastu pierwszych pomiarów, dlatego do obliczenia stycznych w zakresie liniowym nie zostały uwzględnione. O cechach materiału świadczy złom , który jest kruchy doraźny, nie występuje deformacja materiału. Ze względu na liczne źródła karbów wewnętrznych żeliwo nie stosuje się na konstrukcje narażone na pękanie.

3

---