Przedmiot - Fizyka (30 godzin wykładu + 30 godzin ćwiczeń)

Wykładowca: dr hab. Jacek Wierzchowski (p. 103).

Czym jest fizyka?

Fizyka jest nauką przyrodniczą, posługującą się metodą doświadczalną.

Jej celem jest wykrycie fundamentalnych praw o charakterze ilościowym, rządzących zachowaniem materii, oraz poznanie elementarnych składników materii.

Fizyka jest podstawową nauką dla szeregu innych nauk przyrodniczych (“nauk szczegółowych”), w tym chemii. Redukcjonizm (teoriopoznawczy) to pogląd, według którego prawa innych nauk przyrodniczych dają się wyprowadzić z praw fizyki lub przynajmniej nie mogą być z nimi sprzeczne.

Fizyka formułuje prawa i teorie (lub modele*) fizyczne, które pozwalają na ilościowe przewidywania przebiegu zjawisk. Przewidywania te są sprawdzane na drodze doświadczalnej, tj. poprzez obserwację lub doświadczenie, których istotnym elementem są zawsze pomiary wielkości fizycznych.

*modele fizyczne zjawisk są mniej ścisłe od teorii i zawierają zwykle szereg uproszczeń. Stosuje się je do zagadnień b. skomplikowanych (np. reakcji chemicznych czy zjawisk biologicznych).

Obserwacja → SPADANIE CIAŁ

▼

Uogólnienie obserwacji → Spadanie, rzut poziomy, rzut poziomy na kulistej Ziemi

→ ruch orbitalny planet (Kepler)

▼

Prawo fizyczne → Prawo powszechnego ciążenia (Newton)

▼

Teoria fizyczna → Mechanika klasyczna (Newton, Lagrange, Euler i in.)Fizyka a matematyka.

Wg. Galileusza, “Księga przyrody napisana jest w języku matematyki”, zatem głównym narzędziem fizyki jest matematyka. Wiele praw i teorii fizycznych sformułowanych jest w języku równań różniczkowych (i/lub całkowych), które można rozwiązywać analitycznie lub numerycznie. W większości wypadków rozwiązania te mają charakter przybliżony*, ale w wielu wypadkach pozwalają przewidywać nieznane wcześniej fakty (np. odkrycie dalekich planet, fal radiowych, antyelektronu itd.)

Należy jednak pamiętać, że ostatecznym sprawdzianem słuszności teorii fizycznej jest doświadczenie!

*Równania różniczkowe i całkowe różnią się m. in. tym od zwykłych równań, że ich rozwiązania nie są liczbami, lecz funkcjami (lub rodzinami funkcji).

Czy prawa fizyki są ścisłe?

Niektóre ze znanych teorii fizycznych wydają się nam zupełnie ścisłe (tzn. nie stwierdzono doświadczalnie rozbieżności miedzy teorią a eksperymentem. Taką teorią jest np. ogólna teoria względności i elektrodynamika kwantowa. To się może jednak w przyszłości zmienić, kiedy poznamy nowe fakty doświadczalne. Jednak już dzisiaj większość praw fizyki ma charakter przybliżony - są one słuszne w ograniczonym zakresie.

--------

Działy fizyki:

Fizyka klasyczna: Fizyka “współczesna” (XX w.):

Mechanika klasyczna (XVII-XIX w.) Fizyka i astrofizyka relatywistyczna

Termodynamika (XVII-XIX w.) Mechanika i elektrodynamika kwantowa

Elektrodynamika (XIX w.) Fizyka cząstek elementarnych, fizyka jądrowa

Optyka klasyczna (XVII-XIX w.) Optyka kwantowa i spektroskopia

Chemia kwantowa

Fizyka ciała stałego itd.

Nauki pokrewne fizyce:

Astrofizyka, Astronomia, Geofizyka, Fizykochemia (“Chemical Physics” lub „Physical Chemistry”), Biofizyka, Fizyka medyczna i in.

Metody fizyczne stosowane są dziś niemal w każdej dyscyplinie naukowej, zarówno w naukach podstawowych jak i technicznych.

W szczególności, chemia jest już dzisiaj niemalże działem fizyki, gdyż teorie fizyczne (=teorię kwantów) stosuje się do przewidywania własności (rozmiarów, kształtów, energii itd.) cząsteczek chemicznych.. Również analiza chemiczna nie byłaby możliwa bez takich metod fizycznych jak spektrometria masowa czy spektroskopia.

Ogromny postęp w naukach biologicznych zawdzięczamy także stosowaniu metod fizycznych i fizykochemicznych, np.:

- dyfrakcja promieni Roentgena (struktura DNA, struktura białek)

- spektroskopia rezonansu magnetycznego (NMR, EPR) .

- spektroskopia klasyczna i laserowa (działanie światła na organizmy)

- mikroskopia optyczna i elektronowa, mikroskopia sił atomowych,

- metody izotopowe, autoradiografia

- chromatografia, elektroforeza (rozdział i analiza skomplikowanych mieszanin)

- metody hydrodynamiczne (wirowanie, wiskozymetria)

oraz wiele innych.

Podobnie jest w naukach medycznych.

W naukach technicznych udział fizyki jest oczywisty.

W nauce o żywności wykorzystujemy metody analizy chemicznej i fizycznej, a także metody typowe dla nauk biologicznych.

Program wykładu

1. Wiadomości wprowadzające. Elementy rachunku wektorowego i analizy matematycznej. Pomiary fizyczne i teoria opracowania wyników.

2. Opis ruchu. Zasady dynamiki i siły rzeczywiste. Zasady zachowania wielkości dynamicznych.

3. Mechanika bryły sztywnej

4. Reologia (mechanika cieczy i gazów).

5. Drgania i fale.

6. Elementy fizyki cząsteczkowej i termodynamiki

7. Elementy elektrodynamiki.

8. Promieniowanie elektromagnetyczne i jego oddziaływanie z materią.

9. Elementy teorii kwantów i jej zastosowania: spektroskopia, teoria półprzewodników.

10. Elementy fizyki jądrowej: promieniowanie jonizujące, energetyka jądrowa.

Literatura:

1. David Halliday, Robert Resnick, Jearl Walker, Podstawy fizyki, t. 1-5, WN PWN.

2. David Halliday, Robert Resnick, Fizyka t. 1-2. (dla politechnik).

3. M. Skorko, Fizyka.

4. S. Przestalski, Fizyka z elementami bio- i agrofizyki (dla uczelni rolniczych)

5. Hewitt, Fizyka wokół nas (poziom elementarny)

6. Podręczniki z zakresu szkoły średniej!

7. A.K. Wróbewski, Historia Fizyki

Literatura do ćwiczeń: R. Drabent i in., Ćwiczenia laboratoryjne z fizyki, Olsztyn, 2003.

Trochę matematyki

Funkcje elementarne:

Funkcje potęgowe, wielomianowe i ułamkowe:

należy pamiętać, że:

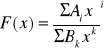
Funkcje trygonometryczne:

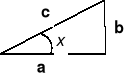
Funkcje wykładnicze i logarytmy:

; e = 2.718....

logarytm jest funkcją odwrotną do funkcji wykładniczej:

Przykłady: 10⁵ = 100000; 10^-3 = 0.001; 10⁰ = 1

log(100000) = 5 log(1) = 0 log(0.001) = -3

Funkcje: wykładnicza i logarytmiczna

Wektory w przestrzeni 3-wymiarowej

Wektory są tworami matematycznymi. Doświadczenie pokazuje jednak, że wiele wielkości fizycznych zachowuje się jak wektory

Sposób przedstawiania wektorów: najczęściej wektory przedstawiamy w kartezjańskim układzie współrzędnych prostokątnych:

graficznie:

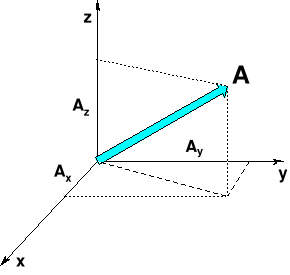
lub analitycznie: A = (A_x, A_y, A_z)

lub: A = i_xA_x + i_yA_y + i_zA_z

lub: A = iA_x + jA_y + kA_z

gdzie i,j,k (i_x,i_y,i_z) są wektorami jednostkowymi (wersorami) o kierunkach osi x, y i z.

długość wektora definiuje się jako: ║A║ =

Dodawanie wektorów definiujemy wg. prawa równoległoboku lub analitycznie:

A + B = (A_x, A_y, A_z) + (B_x, B_y, B_z) = (A_x + B_x, A_y + B_y, A_z + B_z)

Mnożenie wektora przez liczbę (skalar):

x^.A = x^.(A_x, A_y, A_z) = (x^.A_x, x^.A_y, x^.A_z)

W rachunku na wektorach zachodzą związki:

A + B = B + A

x^.(A + B) = x^.A + x^.B

(jeśli x - liczba)

A + (B + C) = (A + B) + C

Tzw. mnożenie wektorów:

Definiujemy następujące operacje na wektorach, w skrócie nazywane „mnożeniem wektorów”. Należy podkreślić, że nie są to zwykłe „działania” na wektorach, ponieważ nie spełniają niektórych twierdzeń typowych dla działań na liczbach.

Iloczyn skalarny wektorów

(wynik tej operacji jest skalarem, czyli liczbą, zatem nie jest to „działanie” na wektorach, nie da się również określić działania odwrotnego, tj. dzielenia)

definicja 1: A∙B = A_x∙B_x + A_y∙B_y + A_z∙B_z

definicja 2 (równoważna): A∙B = ║A║∙║B║∙cos(A,B)

Najważniejsze własności iloczynu skalarnego:

A∙B = B∙A; A∙(B+C) = A∙B + A∙C

A·A = ║A║² = A_x² + A_y² + A_z²

Iloczyn skalarny dwóch wektorów prostopadłych jest zerem!

Bo cos(90^o) = 0

Iloczyn wektorowy 2 wektorów

(wynik jest wektorem, ale nie można określić działania odwrotnego, czyli dzielenia)

definicja 1: A×B = (A_y∙B_z - A_z∙B_y , A_z∙B_x - A_x∙B_z , A_x∙B_y - A_y∙B_x)

definicja 2 (równoważna): ║A×B║ = ║A║∙║B║∙sin(A,B)

kierunek wektora A×B jest prostopadły do A i B; zaś jego zwrot określony jest regułą śruby prawoskrętnej

(z tej definicji wynika brak przemienności)

Najważniejsze własności iloczynu wektorowego:

A×B = -B×A

A× (B+C) = A×B + A×C

A×(B×C) = B(A∙C) - C(A·B)

Iloczyn wektorowy dwóch wektorów równoległych jest zerem

Zastosowanie: np. w ruchu obrotowym

V = R×ω

W opisie pola magnetycznego itd.

Rachunek różniczkowy i całkowy w fizyce

Uwaga historyczna: Rozwój historyczny fizyki klasycznej i analizy matematycznej przebiegał równolegle, gdyż okazało się, że najprostszym sposobem wyrażania ilościowych praw fizyki i korzystania z nich jest zastosowanie rachunku różniczkowego i całkowego oraz analizy wektorowej. Analiza matematyczna (rachunek wektorowy oraz różniczkowy i całkowy) została rozwinięta w XVII-XVIII w. głównie na użytek fizyki (mechaniki klasycznej). Jej twórcami byli często fizycy, jak Newton, Laplace, a także znani filozofowie jak Pascal, Kartezjusz, Euler, Leibniz, d'Alembert i in.

Przypomnienie: pochodna funkcji F(x) w punkcie x₀ jest zdefiniowana jako:

albo

i oznaczana: F'(x) lub

Przykłady: prędkość jest pochodną po czasie z funkcji położenia ciała;

przyspieszenie jest pochodną prędkości po czasie

Uwaga: Dla funkcji wielu zmiennych używamy pojęcia pochodnych cząstkowych, np.
. Pochodne te obliczamy zupełnie tak samo, jak pochodne „zupełne”.

Główne twierdzenia umożliwiające różniczkowanie (czyli obliczanie pochodnych) danej funkcji to:

(aF(x) + bG(x)) = a
+b
(a,b - stałe)

(F(x)·G(x)) = G(x)
+F(x)

(F(G(x)) =
^.

TO JEST ŁATWE

Oczywiście, jeśli się wie, jak obliczyć pochodne funkcji elementarnych. A można to zrobić tak:

Różniczkowanie funkcji wektorowej o argumencie skalarnym A(t) określone jest analogicznie jak różniczkowanie trzech funkcji skalarnych, tj.

A(t) = (
,
,
)

Można łatwo pokazać, że jeśli a,b - stałe liczby, to:

(aA(t) + bB(t)) = a
+ b

= A·
+ B·

= A×
+ B×

Całkę oznaczoną z funkcji F(x) definiujemy jako pole pod krzywą między wybranymi punktami a i b, zwanymi granicami całkowania, które obliczamy jako:

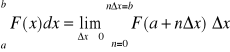
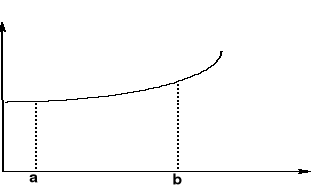
Całka oznaczona jest liczbą; natomiast całka nieoznaczona jest funkcją, w której stała b została zastąpiona przez zmienną x.

Twierdzenie podstawowe rachunku różniczkowego i całkowego

Całkowanie jest operacja odwrotną do różniczkowania, tzn. jeśli funkcja F(x) może być wyrażona jako pochodna innej funkcji G(x), tzn.

F(x)=

to funkcja G wyraża się jako całka z funkcji F:

G(x)-G(a) =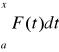
(całka oznaczona) lub

G(x) = ∫F(x)dx + const (całka nieoznaczona)

Powyższe twierdzenie umożliwia obliczanie całek z wielu funkcji F, np. poprzez zgadnięcie odpowiedniej funkcji G. Istnieją jednak funkcje „niecałkowalne”, tzn. takie, dla których funkcja G nie da się zapisać jako kombinacja funkcji elementarnych (wielomian, ułamek, logarytm, funkcje wykładnicze i trygonometryczne).

POMIARY FIZYCZNE

Pomiary wielkości fizycznych są elementem każdego doświadczenia. Pomiary polegają na porównywaniu mierzonej wielkości fizycznej z odpowiednimi wzorcami (jednostkami). Każdy pomiar jest obarczony błędem pomiarowym (zwanym też niepewnością pomiaru).

Dla wybranych wielkości fizycznych ustalono wzorce fizyczne (jednostki podstawowe). Jednostki innych wielkości (jednostki pochodne) określa się jako kombinacje jednostek podstawowych, posługując się znanymi zależnościami fizycznymi, np. dla prędkości jednostką jest najczęściej m/s. Istnieje wiele układów jednostek podstawowych i pochodnych; obecnie układem najczęściej używanym jest układ SI, którego jednostkami podstawowymi są:

metr m długość

sekunda s czas

kilogram kg masa

amper A natężenie prądu

kelwin K temperatura bezwzględna

kandela cd światłość

Dla innych wielkości fizycznych określa się jednostki pochodne, np. jednostką energii dżul (1 J = 1 kg∙m²/s²). Określenie jednostek wielkości pochodnych jest zwykle zgodne z definicjami (wzorami definicyjnymi) tychże wielkości.

Układ SI dopuszcza także jednostki wielokrotne i podwielokrotne; które oznacza się przedrostkami, np.

kilo- (10³); mega- (10⁶); giga- (10⁹);

mili- (10^-3); mikro- (10^-6); nano- (10^-9); piko-(10^-12) itd

Wzorce podstawowych wielkości mechanicznych

Istnieje tendencja, by wzorce wielkości fizycznych były oparte o naturalne procesy, np. oscylacje atomowe. Wzorce takie (np. zegar cezowy) są uniwersalne i łatwo dostępne. Nie zawsze jednak jest to możliwe, i niekiedy z powodów technicznych wygodniej jest używać wzorce umowne, jak np. wzorzec kilograma.

metr - 1650763,73 - krotność długości fali emitowanego przez atom ⁸⁶Kr przy przejściu elektronowym 2p₁₀ - 5d₅

rozmiar Wszechświata - 10²⁴ m rozmiar protonu - 10^-15 m

sekunda - 9192631,770 okresów drgań przejścia nadsubtelnego w atomie ¹³³Cs (zegar cezowy)

wiek Wszechświata - 5∙10¹⁷ s najkrótszy impuls światła - 10^-15 s

kilogram - masa równa masie wzorca kilograma, przechowywanego w Międzynarodowym biurze Wzorców.

masa Galaktyki - 2∙10²⁴ kg; masa elektronu - 9,1∙10^-31 kg

wzorzec ampera będzie objaśniony w dalszych częściach wykładu

Analiza niepewności pomiarów

Najczęściej używane pojęcia i wzory z zakresu rachunku niepewności pomiarów (czyli tzw. „rachunku błędów”):

Uwaga: pojęcia „niepewność pomiaru” i „błąd pomiaru” używane są wymiennie.

Błąd przypadkowy - błąd, który przy powtarzaniu pomiarów prowadzi do rozrzutu statystycznego wyników wokół wartości prawdziwej, którą można obliczyć jako średnią

Błąd systematyczny - błąd, który przy powtarzaniu pomiarów nie prowadzi do rozrzutu statystycznego wyników, ale w sposób systematyczny deformuje wartość średnią wyników

Błąd gruby - wielkość X zmierzona pomyłkowo w wyniku błędnie wykonanego eksperymentu (nie uwzględniamy w analizie)

Poziom ufności błędu (oceny niepewności) - mówimy, że wielkość X zmierzona jest z niepewnością (błędem) ΔX na poziomie ufności P (P ≤ 1), jeśli z prawdopodobieństwem P wiadomo, że prawdziwa wielkość wielkości X zawarta jest w przedziale [X ± ΔX].

Błąd standardowy - błąd (niepewność) obliczony na poziomie ufności 68.3% (tzw. poziomie standardowym). Jest to poziom odpowiadający odchyleniu standardowemu (σ) w rozkładzie normalnym błędów.

Błąd bezwzględny - błąd (niepewność) pomiaru wyrażony w jednostkach wielkości mierzonej (ΔX).

Błąd względny - stosunek błędu (niepewności) bezwzględnego do wielkości mierzonej (ΔX/X). Niekiedy wyrażany jest on w procentach.

Jeżeli wyniki eksperymentu wykazują rozrzut (błędy przypadkowe), to do oceny błędu stosujemy analizę statystyczną. Najczęściej zakłada się, że rozrzut wyników jest zgodny z rozkładem normalnym (rozkładem Gaussa) wokół wartości średniej, którą uznajemy umownie za „prawdziwą” wartość mierzonego parametru x:

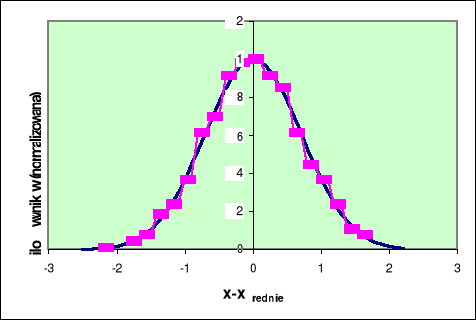
Uwaga: wartość prawdziwa może pokrywać się ze średnią (x_średnie) - błąd przypadkowy

lub może być różna od x_średnie (jeśli dochodzi błąd systematyczny)

Jeżeli rozrzut n wyników pomiarów tej samej wielkości jest przypadkowy, nie występują błędy systematyczne, a wszystkie pomiary są wykonane w identycznych warunkach i niezależnie od siebie, to za wynik najbardziej prawdopodobny uznajemy średnią arytmetyczną uzyskanych wyników:

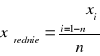
natomiast niepewność wyniku (wartości średniej) na poziomie standardowym (68.3%) określa wzór:

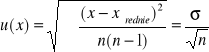
Uwaga: wielkość

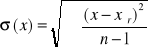
jest dyspersją rozrzutu i nie zależy od liczby powtórzeń (n).

Uwaga: Rozkład normalny stosuje się ściśle tylko przy wielkiej liczbie powtórzeńRozkład prostokątny wyników pomiarowych (uzyskiwany, jeśli wynik pomiaru powtarza się, a przyrząd ma określoną dokładność ΔX):

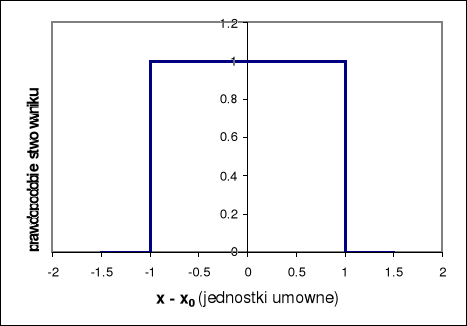
na powyższym rysunku przyjęto ΔX = 1.

W tym wypadku bezpośrednio (np. z instrukcji przyrządu pomiarowego lub klasy przyrządu, ew. z najmniejszej podziałki skali) znamy niepewność pomiaru na poziomie ufności 100%, czyli tzw. błąd maksymalny pomiaru ΔX. Aby przejść na standardowy poziom ufności (68.3%), stosujemy wzór:

Analiza dokładności pomiarów złożonych

Zwykle pomiary fizyczne są pomiarami złożonymi, tzn. ostateczny wynik doświadczenia otrzymujemy po obliczeniu wielkości mierzonej z tzw. wzoru roboczego, mającego postać:

gdzie f - zależność funkcyjna, wielkości X,Y,Z są bezpośrednio zmierzone z określonymi dokładnościami ΔX, ΔY, ΔZ, natomiast a, b, c - parametrami wziętymi z tablic lub teorii (niepewność określenia tych wielkości jest do zaniedbania w danych warunkach).

Twierdzenie: Jeżeli błędy (niepewności) ΔX, ΔY, ΔZ są określone na poziomie standardowym, oraz są od siebie niezależne, to niepewność wielkości obliczonej A wyraża się wzorem (zwanym niekiedy „wzorem na różniczkę zupełną”):

Wielkości
,
itd. są pochodnymi cząstkowymi funkcji f względem wielkości X.

Przykład:

Obliczamy gęstość kulki ρ, na podstawie zmierzonej średnicy d oraz masy m. Stosujemy wzór roboczy:

obliczając pochodne cząstkowe względem masy oraz średnicy, i stosując wzór na „różniczkę zupełną” dostajemy wynik:

Zauważmy, że wynik powyższy daje się przepisać w formie uproszczonej:

ponieważ

oraz

Uwaga: wzór uproszczony daje się stosować tylko w niektórych przypadkach!!!Zaokrąglanie wyników pomiarów i obliczeń

Wyniki pomiarów, po przeprowadzonych obliczeniach, należy zaokrąglić. Prawidłowe zaokrąglenie wyników musi uwzględniać niepewność (błąd) pomiaru.

Najczęściej w wyniku obliczeń na komputerze lub kalkulatorze otrzymujemy wynik w postaci niezaokrąglonej, np.

x = 2175,5640219

aby prawidłowo zaokrąglić ten wynik, należy znać wielkość błędu (niepewności). Należy przy tym pamiętać, że wartość błędu jest zawsze tylko szacunkowa i wobec tego nie ma sensu podawać jej ze zbyt dużą dokładnością. Jeżeli z obliczeń otrzymujemy wartość błędu:

Δx = 5,4673201

to zaokrąglamy ją podając co najwyżej 2 cyfry znaczące:

Δx ≈5,5

jeżeli pierwsza cyfra znacząca wynosi 5 lub więcej, to można zaokrąglić błąd do 1 cyfry:

Δx ≈ 6

natomiast samą wartość mierzoną zaokrąglamy zgodnie z zaokrągleniem błędu i zapisujemy:

x = 2175,6 ± 5,5

lub:

x = 2176 ± 6

Czasami stosuje się również inny, równoważny zapis:

x = 2176(6)

Inne przykłady zaokrągleń:

Wielkość niezaokrąglona: błąd: prawidłowy zapis:

0,004567982 0,000012594 0,004568 ± 0,000013 lub

0,004568(13)

168945273,34 535,02 168945270 ± 540 lub

1,6894527(54)·10⁸

Kinematyka punktu materialnego

Pojęcia podstawowe:

Ruch - to zmiana położenia (lub kształtu) ciał fizycznych w czasie. Kinematyka jest nauką o ruchu ciał i jego opisie matematycznym. Ruch jest względny, tzn. jego opis zależy od wybranego układu odniesienia.

Ciała fizyczne są obiektami złożonymi i ich opis ruchu jest na ogół skomplikowany. Jednak w wielu wypadkach ciała te możemy w przybliżeniu traktować jako punkty materialne.
Punkt materialny to taki (hipotetyczny) obiekt fizyczny, którego ruch daje się opisać w sposób pełny przez podanie funkcji wektorowej czasu, r(t), zwanej funkcją położenia lub wektorem wodzącym punktu materialnego. Wektor ten najczęściej wyraża się w układzie współrzędnych prostokątnych (kartezjańskich), w tym wypadku są to trzy funkcje skalarne: (x(t),y(t),z(t)). Punkt materialny nie ma zatem żadnych „ruchów wewnętrznych”.

Np. cząstki elementarne (elektron, proton, neutron) można niekiedy traktować jak punkty materialne.

Torem ruchu nazywamy krzywą opisaną parametrycznie przez wektor położenia r(t).

Możliwy (i niekiedy celowy) jest także opis ruchu we współrzędnych krzywoliniowych, np. kulistych (r,,) lub walcowych (ρ,,z).

Ruch opisuje się również przy użyciu pojęć prędkości i przyspieszenia.

Prędkość (rzeczywista, czyli chwilowa) jest zdefiniowana jako wektor:

v(t) =
r(t) = (
,
,
)

Uwaga: wektor prędkości jest zawsze styczny do toru ruchu.

Przyspieszenie (rzeczywiste, czyli chwilowe) definiuje się jako pochodną prędkości, lub drugą pochodną położenia:

a(t) =
v(t) = (
,
,
) = (
,
,
)

Jak widać, mając daną funkcję wektorową r(t) = (x(t),y(t),z(t)), możemy zawsze w sposób jednoznaczny policzyć wektory v(t) i a(t), wykonując odpowiednie różniczkowania.

Widać też, że we współrzędnych prostokątnych poszczególne współrzędne ruchu - x,y,z - są różniczkowane niezależnie, tzn. x-owe składowe wektorów v i a zależą tylko od x-owej składowej wektora r(t). Fakt ten nazywany jest zasadą niezależności ruchów. Jest on potwierdzony doświadczalnie.

Mając daną funkcję wektorową v(t) lub a(t) możemy obliczać położenie ciał jako funkcję czasu, czyli funkcję r(t), stosując twierdzenie podstawowe rachunku różniczkowego i całkowego:

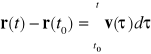
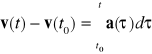
(gdzie całkowanie poszczególnych składowych wektorów jest znów niezależne)

Możemy również próbować rozwiązywać ten problem metodą „zgadnięcia”.

Należy jednak pamiętać, że procedura całkowania nie jest całkowicie jednoznaczna - wymaga ona podania tzw. warunków początkowych ruchu, tj. wartości liczbowych wektorów r(t₀) i/lub v(t₀). Wynika to stad, że pochodna stałej jest zerem. Najczęściej przyjmujemy t₀ =0, i oznaczamy r(0) = r₀ v(0) = v₀

Prędkość i przyspieszenie średnie. Ogólny wzór na prędkość średnią w czasie t₁ do t₂ jest następujący:

v_śr(t₁,t₂)- =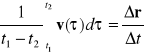
a średnie przyspieszenie: a_śr(t₁,t₂)- =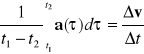

Przykłady

Najprostszym ruchem (oprócz spoczynku) jest ruch jednostajny po prostej.

Jest to ruch jednowymiarowy, gdyż zawsze można wybrać taki układ współrzędnych, że jedna z jego osi (np. oś x) pokryje się z kierunkiem ruchu. Wówczas:

v = (v,0,0)

r(t) = (x(t),0,0) = (vt + B,0,0)

stała B jest dowolna; jest oczywiste, że B = x(0).

Ruchem jednostajnie przyspieszonym prostoliniowym nazywa się ruch po prostej, gdzie a = const = (a,0,0). Można policzyć (lub odgadnąć) funkcje v(t) i x(t):

v(t) = at + C, gdzie C = v(0) jest stała dowolną,

x(t) = at²/2 + v(0)t + B, gdzie B = x(0)

jak widać, w tym ruchu występują już dwie stałe dowolne, v(0) i x(0), które musimy określić, podając warunki początkowe ruchu.

Złożenie ruchu jednostajnie przyspieszonego wzdłuż osi x z ruchem jednostajnym wzdłuż osi y (lub z) daje “rzut ukośny”, który jest przykładem ruchu dwuwymiarowego:

a = (a,0,0)

v = (v_x,v_y,0) = (at + v_x(0), v_y(0), 0)

r = (x,y,z) = (at²/2 + v_x(0)t + x(0), v_y(0)t + y(0), 0)

Torem tego ruchu jest parabola. Jak widać, jednoznaczne określenie tego ruchu wymaga podania czterech warunków początkowych: v_x(0), v_y(0), x(0), i y(0). Jeśli wartość początkowa v_y(0) = 0 to mamy “rzut poziomy”.

Ruch po okręgu

Równania tego ruchu można sformułować we współrzędnych x,y (jest to ruch dwuwymiarowy):

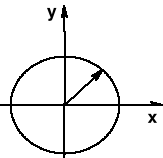
r(t) = (x(t),y(t),0) = (Rcos(t), Rsin(t), 0)

gdzie  jest kątem (mierzonym w radianach) między wektorem wodzącym punktu a osią y. Jak widać, |r| = R = const. Jeśli rozważamy ruch jednostajny po okręgu, to

(t) = t + ₀

gdzie  (częstość kołowa lub prędkość kątowa) jest stałą związaną z okresem obiegu, łatwo pokazać, ze:  = 2/T, gdzie T - okres obiegu. Wymiarem stałej  są radiany na sekundę (lub 1/s).

Prędkość w ruchu po okręgu liczymy, różniczkując r(t):

v(t) =
{R[cos(t), sin(t)]} = R[-sin(t)], cos(t)]·

Wielkość
nazywamy chwilową prędkością kątową i wyrażamy w radianach na sekundę. Dla ruchu jednostajnego po okręgu
=   constans

Wartość prędkości w ruchu po okręgu obliczamy ze wzoru:

|v| =
= R
, a w ruchu jednostajnym Rω= constans

Prędkość v(t) jest w ruchu po okręgu zawsze prostopadła do r (bo musi być styczna do toru), co pokazujemy obliczając iloczyn skalarny:

r·v =
R²(sincoscossin = 0

Jest to, jak widać, prawdziwe nawet wtedy, gdy ruch po okręgu nie jest jednostajny.

Przyspieszenie w ruchu po okręgu liczymy, różniczkując v(t).

W przypadku ruchu jednostajnego po okręgu dostajemy:

a(t) =
{R[-sin(t + ₀), cos(t + ₀)]}= - ^R[cos(t + ₀), sin(t + ₀)] = - ^r(t)

zatem przyspieszenie w ruchu jednostajnym po okręgu ma kierunek taki sam, jak promień, lecz odmienny zwrot (jest to przyspieszenie dośrodkowe). Jego wartość wynosi ^R.

Jeśli jednak ruch po okręgu nie jest jednostajny, to na ogół kierunki wektorów a(t) i r(t) nie będą zgodne, gdyż:

a(t) =
{R
[-sin(t),cos(t)]} = - (
)^R[cos(t), sin(t)] + R
[-sin(t),cos(t)]

pierwszy składnik powyższej sumy ma kierunek przeciwny do kierunku r, i wyraża przyspieszenie dośrodkowe, gdyż
można uważać za chwilową prędkość kątową (t), ale drugi składnik ma kierunek zgodny z wektorem prędkości, a więc jest styczny do toru. Wielkość
jest równa chwilowemu przyspieszeniu kątowemu (), zatem sumarycznie:

a(t) = -(t)^r(t) + Ri_t(t),

gdzie i_t(t) jest wektorem jednostkowym (wersorem) stycznym do ruchu.

Jest to ogólny wzór na przyspieszenie w ruchu po okręgu. Jak się okazuje, ma on również zastosowanie do każdego ruchu krzywoliniowego, z tym, że w tym ostatnim wypadku R jest chwilowym promieniem krzywizny ruchu.

Opis ruchu w różnych układach odniesienia. Niezmienniczość praw fizyki

Ruch można opisywać w różnych układach odniesienia (czyli jest względny). Procedura matematyczna, pozwalająca na przechodzenie z jednego układu odniesienia do innego, nazywana jest transformacją układu odniesienia. Najprostsza transformacją jest transformacja Galileusza, która mówi miedzy innymi, że prędkość układu odniesienia dodaje się wektorowo do prędkości ciała w starym układzie:

v' = v - V_układu

Zauważmy, że jeżeli prędkość układu jest stała, to przyspieszenie ciała jest identyczne w układzie „ruchomym” i „nieruchomym”. Jest to zatem wielkość niezmiennicza względem transformacji Galileusza.

Wg. postulatu niezmienniczości Galileusza

wszystkie podstawowe prawa fizyczne (teorie) powinny być formułowane tak, by nie zależały od układu odniesienia.

(tzn. zawierały tylko wielkości niezmiennicze względem tzw. transformacji Galileusza).

Warunek niezmienniczości praw fizyki oznacza, że żaden układ odniesienia nie może być wyróżniony (dokładniej: żaden inercjalny układ odniesienia, zob. następny wykład). Mechanika klasyczna spełnia ten warunek.

Okazało się, że postulat Galileusza nie może być zrealizowany ściśle, w szczególności ze względu na zjawiska elektromagnetyczne. W końcu XIX w. Lorentz zaproponował inną, bardziej skomplikowaną matematycznie i pojęciowo procedurę transformacji, tj. przechodzenia od jednego układu odniesienia do innego. Wmyśl tej transformacji, prędkości układu odniesienia nie dodają się liniowo do prędkości ciała. Obecnie uważamy, że wszystkie prawa fizyki powinny być niezmiennicze względem transformacji Lorentza, a nie Galileusza. Postulat ten wprowadził Einstein w 1905 roku.

Dynamika punktu materialnego

Dynamika jest to nauka o ruchu z uwzględnieniem jego przyczyn. Pojęcia podstawowe dynamiki to masa, siła i pęd. Ważnym pojęciem jest także

Pojęcie układu inercjalnego: pojęcie to określa pierwsza zasada dynamiki Newtona, która mówi, że istnieje taki układ odniesienia, w którym ciało nie oddziaływujące z innymi ciałami pozostaje w spoczynku lub porusza się ruchem jednostajnym. Z prawa transformacji Galileusza wynika, że każdy układ poruszający się ruchem jednostajnym względem układu inercjalnego jest także układem inercjalnym.

W praktyce nie można w przyrodzie znaleźć układów idealnie inercjalnych, ale wiele układów w dobrym przybliżeniu spełnia warunek inercjalności.

Pojęcie masy definiujemy w sposób operacyjny, tzn. podając sposób pomiaru. Wyobraźmy sobie urządzenie, służące do nadawania ruchu ciałom, tzn. urządzenie przyspieszające (np. wykorzystujące sprężystość). Urządzenie to nada różnym ciałom różne przyspieszenia. Jak wykazuje doświadczenie, stosunek wartości tych przyspieszeń, |a₁|/|a₂|, nie zależy od rodzaju użytego urządzenia, a tylko od ciała przyspieszanego. Tę własność ciał, która „przeciwstawia się” przyspieszeniu nazywamy masą bezwładną i oznaczamy symbolem m, mamy zatem na mocy definicji |a₁|/|a₂| = m₂/m₁.

Z powyższej analizy wynika także, że iloczyny m₁|a₁|= m₂|a₂| charakteryzują działanie urządzeń przyspieszających, są natomiast niezależne od cech ciała przyspieszanego. Uogólnieniem tej obserwacji jest druga zasada dynamiki Newtona:

F = ma

która jednocześnie definiuje pojęcie wektora siły (F) jako miary oddziaływania.

Z doświadczenia wynika, że przy równoczesnym działaniu kilku sił na jedno ciało, jego przyspieszenie jest sumą wektorową przyspieszeń, pochodzących od poszczególnych oddziaływań. Fakt ten znany jest jako zasada superpozycji sił lub zasada niezależności sił. Fakt ten umożliwia stosowanie zasad rachunku wektorowego do analizy złożonych oddziaływań.

Podstawowe zagadnienie dynamiki punktu materialnego.

Sumaryczna siła, działająca na punkt materialny o masie m, może być funkcją jego położenia, prędkości, a także czasu:

F = F(r,v,t)

Jednak zarówno r jak i v są funkcjami czasu (mogą być także funkcjami parametrów ruchu innych ciał, ale fakt ten na razie pomijamy). Biorąc pod uwagę, że:

v(t) =
r(t) oraz a(t) =
r(t),

możemy napisać:

F = ma = m
r(t) = F(r(t),
r(t),t)

Jest to równanie różniczkowe drugiego rzędu pozwalające rozwiązać tzw. podstawowe zagadnienie dynamiki punktu materialnego, tzn. obliczyć ruch przy znanej zależności F(r,v,t). Jest to na ogół zagadnienie skomplikowane i tylko w nielicznych wypadkach daje się ono rozwiązać w sposób analityczny (tzn. przez podanie wzoru). Częściej rozwiązujemy je w sposób numeryczny, tzn. przez podanie wyników liczbowych (np. obliczanie orbit sztucznych satelitów, komet itd.). Podejście numeryczne sprowadza równania różniczkowe do przybliżonych równań algebraicznych.

Inne sformułowania równań ruchu.

Równania ruchu można również wyrazić, wprowadzając pojęcie pędu, p=mv. Wówczas:

F = ma = m
v =
(mv) =
p(t)

W powyższym równaniu założono, że m=const. Jeżeli jednak masa obiektu jest zmienna (np. kropla wody spadająca we mgle), to okazuje się, że równanie F = ma przestaje obowiązywać, a prawdziwe staje się równanie:

F =
p(t)

Możliwe jest również sformułowanie praw dynamiki poprzez tzw. zasady wariacyjne (prowadzą one do równań całkowych, które są równoważne równaniom Newtona).

Trzecia zasada dynamiki Newtona

Oddziaływania zawsze zachodzą między ciałami materialnymi. Jeżeli ciało A działa na ciało B siłą F_AB, to ciało B działa także na ciało A siłą F_BA. Trzecia zasada dynamiki (zwana zasadą akcji i reakcji) mówi, że

F_AB = -F_BA

Czyli są to siły równe co do wartości, lecz przeciwnie skierowane. Zasada ta pozwala na sformułowanie tzw. zagadnienia dynamiki N ciał, tzn. podania równań ruchu dla N ciał oddziaływujących ze sobą siłami zależnymi od położenia (a niekiedy i prędkości) każdej z cząstek.

Przykładem takiego zagadnienia jest ruch planet i mniejszych obiektów w układzie słonecznym.

Oddziaływania fundamentalne.

Chociaż w przyrodzie znanych jest wiele rodzajów sił, to istnieją dowody na to, że wszystkie one są wynikiem istnienia kilku (trzech lub czterech) oddziaływań (sił) fundamentalnych. W świecie makroskopowym istotne są dwa oddziaływania: grawitacyjne, występujące miedzy wszystkimi ciałami, mającymi masę m. Miedzy takimi ciałami działa siła Newtona:

F₁₂ = -r₁₂
, lub (zapis równoważny) F₁₂ = -i₁₂
,

gdzie r₁₂ = r₁- r₂; G jest stałą grawitacji, równą 6.6720^.10^-11 m²/kg²,

Siła grawitacyjna odpowiada m.in. za ruchy orbitalne planet, księżyców, gwiazd itd., a także np. za istnienie czarnych dziur.

Drugą siła o największym znaczeniu jest oddziaływanie elektromagnetyczne, opisywane zwykle przez dwa wektory pól, E i B, których wartości zależą od rozkładu ładunków elektrycznych i prądów w przestrzeni, zaś siła, działająca na ładunek elektryczny e w punkcie r dana jest wzorem:

F(r) = e[E(r) + v×B(r)]

W mikroświecie działają ponadto siły jądrowe, które dzielą się na silne, odpowiedzialne za stabilność jąder atomowych, ich wzbudzenia oraz rozpady radioaktywne typu  (a także świecenie Słońca i gwiazd), oraz słabe, które odpowiadają za rozpad  oraz za oddziaływania lekkich cząstek zwanych neutrinami (powstają one m. in. podczas rozpadów ).

Można określić uniwersalną (bezwymiarową) miarę siły oddziaływań elementarnych, i uszeregować oddziaływania od najsłabszego do najsilniejszego:

grawitacyjne < słabe jądrowe < elektromagnetyczne < silne jądrowe

Większość sił spotykanych w przyrodzie ma pochodzenie elektromagnetyczne.

Należą do nich:

-siły elektrostatyczne i magnetyczne

-siły oporu (tarcie, lepkość), siły sprężystości,

-siły międzymolekularne, siły adhezji i wszelkie siły utrzymujące spoistość ciał stałych, a także

-siły chemiczne, wiążące atomy w cząsteczki,

-siły biomechaniczne (np. siła skurczu mięśnia) itd.

Ruch związany i siły reakcji.

Jeżeli ruch punktu materialnego jest ograniczony do pewnej powierzchni lub krzywej poprzez działanie czynników zewnętrznych, to ruch taki nazywamy ruchem związanym, a krzywe lub powierzchnie, po których ruch się odbywa nazywamy więzami ruchu. (Przykłady: wahadło matematyczne, ruch po równi pochyłej itd). Występują wówczas siły, które zmuszają punkt do pozostania na zadanej powierzchni lub krzywej. Są to tzw. siły reakcji. Można udowodnić, że

o ile więzy są nieruchome, to siły reakcji są zawsze prostopadłe do więzów (i w związku z tym nie wykonują pracy, zob. niżej). Np. siła nacisku na równię pochyłą, siła reakcji wahadła itp.

Wahadło odchylone o kąt α przedstawia poniższy rysunek

Dynamika ciał w nieinercjalnych układach odniesienia - siły pozorne

Jeżeli nasz układ odniesienia jest układem nieinercjalnym, tzn. porusza się względem jakiegoś układu inercjalnego z pewnym przyspieszeniem liniowym A oraz z prędkością kątową (na ogół zmienną) (t), to pierwsza i druga zasada Newtona nie obowiązują. Mamy wówczas:

F = ma - F_poz

gdzie F_poz nazywamy siłą pozorną. Jest to tzw. siła nienewtonowska, dla której nie obowiązuje trzecia zasada dynamiki. Wartość i kierunek działania sił pozornych zależą nie tylko od parametrów ruchu naszego układu względem układu inercjalnego (tj. przyspieszenia A oraz prędkości obrotów ), ale i od położenia (r'(t)) i prędkości (v'(t)) badanego punktu materialnego w układzie nieinercjalnym.

Uwaga: wektor prędkości kątowej  ma wartość d/dt ( - chwilowy kąt obrotu układu ruchomego względem nieruchomego), kierunek osi obrotu i zwrot zgodny z regułą śruby prawoskrętnej. Kąt liczony jest zawsze w radianach.

W wypadku Ziemi jest to kierunek zgodny z osią obrotów, czyli prosta łączącą dwa bieguny geograficzne S→N. Prędkość kątowa Ziemi wynosi 2π radianów na dobę, czyli

Jak się okazuje, siłę pozorną wynikającą z nieinercjalności układu można obliczyć w sposób następujący (zob. Wróbewski, Zakrzewski, Wstęp do fizyki, t. 1., str.278 i dalsze):

F_poz = F_B - m
×r'(t) + F_C + F_Odśr

Gdzie:

F_B = -mA - to siła bezwładności (przykład: siła działająca na pasażera w hamującym autobusie);

F_C = -2m ×v'(t) - siła Coriolisa (zwana też siłą bezwładności Coriolisa); siła ta działa, jeśli ciało porusza się względem układu ruchomego (działania tej siły doświadcza np. człowiek poruszający się w zakręcającym autobusie). Ta siła jest również odpowiedzialna za tor wahań wahadła Foucault, za odchylenie kierunku wiatrów wokół cyklonu itd.

F_Odśr = m² r'_v(t) - to siła odśrodkowa; r'_v(t) jest rzutem wektora r' na płaszczyznę prostopadłą do (chwilowej) osi obrotu (tzn. wartość wektora r' jest równa odległości ciała od osi obrotu). Można ją wyrazić równoważnym wzorem F_Odśr = m×(×r'(t)). Ta siła wykorzystana jest np. w wirówkach.

Wyrażenie m
×r'(t) nie ma swojej nazwy, występuje ono tylko wówczas, gdy prędkość obrotów układu ruchomego zmienia się.

36

---