PRZEKSZTAŁCENIA GEOMETRYCZNE

Przekształceniem geometrycznym nazywamy każdą funkcję,

której argumentami i wartościami są punkty płaszczyzny.

Jeśli w przekształceniu geometrycznym punktowi P odpowiada punkt P', to punkt P' nazywamy obrazem punktu P w tym przekształceniu.

Figurę F' otrzymaną w wyniku przekształcenia figury F nazywamy obrazem figury F.

Przekształcenia geometryczne dzielimy na takie, które zachowują kształt i wielkość oraz takie, które nie zachowują tych wielkości.

Przekształcenie, które zachowuje odległość punktów nazywamy izometrią.

Do przekształceń izometrycznych należą :

• Symetria osiowa

• Symetria środkowa

• Przesunięcie o wektor

• obrót

SYMETRIA OSIOWA NA PŁASZCZYŹNIE

Symetrią osiową względem prostej k nazywamy takie przekształcenie płaszczyzny na płaszczyznę, w którym obrazem dowolnego punktu A jest taki punkt A`, że spełnione są następujące warunki:

• punkty A i A` leżą na prostej prostopadłej do prostej k i po obu stronach prostej k

• odległości punktów A i A` od prostej k są równe.

Symetrię osiową względem prostej k oznaczamy

Przykłady:

1. Punkt F jest symetryczny do punktu A względem prostej a

2. Punkt F nie jest symetryczny do punktu A względem prostej a

3. Przykłady trójkątów symetrycznych:

• Trójkąt LMN jest symetryczny do trójkąta ABC względem prostej d leżącej poza trójkątem ABC

• Trójkąt LNC jest symetryczny do trójkąta ABC względem prostej d mającej jeden punkt wspólny z trójkątem ABC

• Trójkąt LMN jest symetryczny do trójkąta ABC względem prostej d przecinającej dwa boki trójkąta ABC

• Trójkąt NBC jest symetryczny do trójkąta ABC względem prostej d leżącej wzdłuż boku trójkąta ABC

4. Czworokąt QRST nie jest symetryczny do czworokąta ABCD

Ćwiczenie 1

Rozwiąż zadanie 3, 4, 7 str. 123 z podręcznika.

SYMETRIA ŚRODKOWA NA PŁASZCZYŹNIE

Symetrią środkową względem punktu S nazywamy takie przekształcenie płaszczyzny na płaszczyznę, w którym obrazem punktu A jest punkt A` taki, że punkt S jest środkiem odcinka AA`.

Symetrię środkową względem punktu S oznaczamy

Przykłady:

1. Punkt B jest symetryczny do punktu A względem punktu C

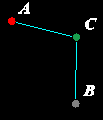
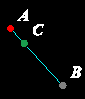
2. Punkt B nie jest symetryczny do punktu A względem punktu C

2. Przykłady trójkątów symetrycznych względem punktu

• Trójkąt GEF jest symetryczny do trójkąta ABC względem punktu D leżącego poza trójkątem ABC

• Trójkąt EDG jest symetryczny do trójkąta ADC względem punktu D będącego wierzchołkiem trójkąta ADC

• Trójkąt EFG jest symetryczny do trójkąta ABC względem punktu D leżącego na boku trójkąta ABC

• Trójkąt EFG jest symetryczny do trójkąta względem punktu D leżącego wewnątrz trójkąta ABC

Ćwiczenie 2

Rozwiąż zadanie 12, 13 str. 124 oraz 14, 18 str. 125 z podręcznika.

TRANSLACJA NA PŁASZCZYŹNIE

Translacją (przesunięciem równoległym) o wektor
nazywamy takie przekształcenie płaszczyzny na płaszczyznę, w którym obrazem punktu A jest taki punkt A`, że wektor AA` jest równy wektorowi
.

Przesunięcie równoległe punktu A o wektor
oznaczamy

Przykłady:

• Punkt B jest obrazem punktu A w translacji o wektor
  

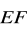
• Punkt B i punkt M nie jest obrazem punktu A w translacji o wektor
  

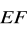
• Trójkąt LMN jest obrazem trójkąta CDE w translacji o wektor
  

Ćwiczenie 3

Rozwiąż zadanie 1, 2 str. 129 z podręcznika.

OBRÓT NA PŁASZCZYŹNIE

Obrotem wokół punktu S o kąt α nazywamy takie przekształcenie płaszczyzny na płaszczyznę, w którym obrazem punktu A jest punkt A` taki, że:

• odcinki SA i SA` są równej długości

• miara kąta ASA` jest równa mierze kąta α.

Obrót wokół punktu S o kąt α oznaczamy

Opisując obrót musimy określić nie tylko, o ile stopni dokonujemy obrotu, ale i kierunek obrotu.

Kąt ujemny kąt dodatni

Punkt K jest obrazem punktu A w obrocie wokół punktu B o kąt ECD

Punkt F nie jest obrazem punktu B w obrocie wokół punktu A o kąt DCE

Przykłady obrotów trójkątów:

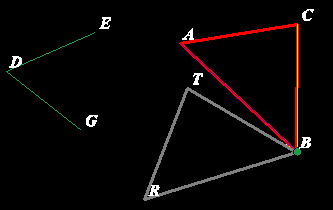
• Trójkąt RST jest obrazem trójkąta ABC w obrocie wokół punktu H leżącego poza trójkątem ABC, o kąt GDE (kąt dodatni)

• Trójkąt RBT jest obrazem trójkąta ABC wokół wierzchołka B o kąt GDE (kąt dodatni),

Trójkąt ABC jest obrazem trójkąta RBT wokół wierzchołka B o kąt EDG (kąt ujemny)

• Trójkąt RST jest obrazem trójkąta ABC wokół punktu H leżącego wewnątrz trójkąta ABC, o kąt GDE (kąt dodatni)

Przykład

Narysuj dowolny kwadrat, a następnie narysuj jego obraz w obrocie wokół jednego z wierzchołków o kąt -90⁰.

D C=A' D'

A B=B' C'

Ćwiczenie 4

Rozwiąż zadanie 5, 6, 7, 8 str. 130 z podręcznika.

SZCZEGÓLNE PRZYPADKI

PRZEKSZTAŁCEŃ GEOMETRYCZNYCH NA PŁASZCZYŹNIE

1. Obrót o kąt 180° wokół punktu O jest symetrią środkową względem punktu O.

2. Translacja o wektor zerowy jest przekształceniem tożsamościowym.

3. Jeżeli istnieje taka prosta, że symetria osiowa względem tej prostej przekształca figurę na nią samą, to figura jest symetryczna osiowo.

4. Jeżeli istnieje punkt taki, że symetria środkowa względem tego punktu przekształca figurę na nią samą, to figura jest symetryczna osiowo.

5. Jeżeli istnieje obrót o kąt mniejszy, od 360°, który przekształca figurę na nią samą, to figura jest symetryczna obrotowo

---