1. Sprawdzenie współczynnika przenikania ciepła Uk (z rysunkami rozkładu temperatur).

Dane:

Ti=25°C

• pomieszczenie wewnętrzne- łazienka

Te= -16°C

• budynek zlokalizowany jest w Mielnie (I strefa klimatyczna)

od lewej

1. tynk cementowo - wapienny- d1=0,015 m, λ=0,82

2. cegła klinkierówka- d2=0,12 m, λ=1,05

3. styropian- d3=0,06 m, λ=0,045

4. cegła dziurawka- d4=0,25 m, λ=0,62

5. tynk cementowo - wapienny- d5=0,015 m, λ=0,82

• Całkowity współczynnik przenikania ciepła

gdzie:

Uo- współczynnik przenikania ciepła

ΔUo- człon korekcyjny współczynnika przenikania ciepła

ΔU- dodatek do współczynnika wyrażający wpływ mostków cieplnych

1. Współczynnik przenikania ciepła Uo

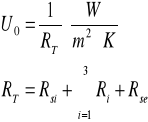
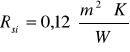
- opór przejmowania ciepła na wewnętrznej powierzchni

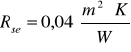
- opór przejmowania ciepła na zewnętrznej powierzchni

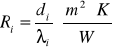
- opór cieplny jednorodnej warstwy materiału

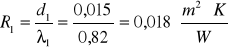
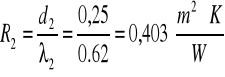
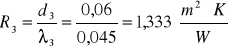
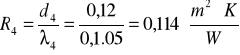
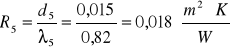
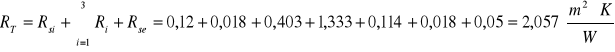
2. poprawki w odniesieniu do współczynnika przenikania ciepła ΔUo

ΔUo=ΔUg+ΔUf

gdzie:

ΔUg- poprawka z uwagi na nieszczelności,

ΔUo- poprawka z uwagi na łączniki mechaniczne.

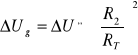
Mamy:

ΔU''=0,01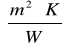
- 1 poziom poprawki

R3=1,333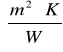
- opór cieplny warstwy zawierającej nieszczelności

RT=2,057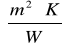
-całkowity opór komponentu

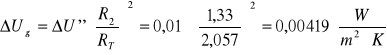
Mamy:

α=6
- współczynnik

- współczynnik przewodzenia ciepła łącznika

- liczba łączników na

- pole powierzchni przekroju łącznika (kotew ∅6)

C. Dodatek wyrażający wpływ mostków cieplnych

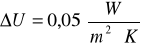
• Całkowity współczynnik przenikania ciepła

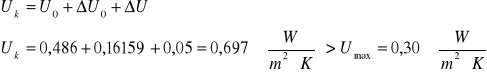
4. Rozkład temperatury na przegrodzie

gdzie:

- temperatura wewnętrznej powierzchni przegrody

- opór przejmowania ciepła na wewnętrznej powierzchni kolejnej przegrody

Mamy:

,

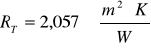
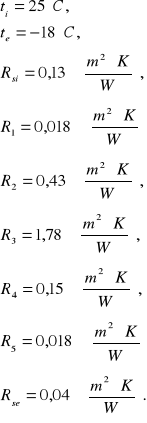
Stąd:

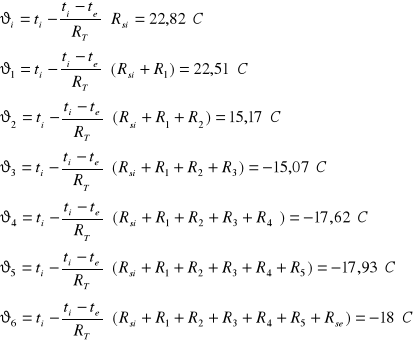
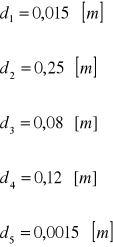
2. Sprawdzenie możliwości roszenia na powierzchni wewnętrznej przegrody

Dane:

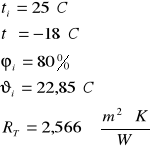
• Temperatura na powierzchni ściany od strony pomieszczenia:

- ciśnienie cząsteczkowe pary wodnej nasyconej przy temperaturze

Ciśnienie cząsteczkowe pary wodnej w pomieszczeniu

Dla wyznaczonego ciśnienia odczytano temperaturę punktu rosy:

• Sprawdzenie możliwości roszenia na powierzchni wewnętrznej przegrody

Ponieważ zachodzi warunek
, na powierzchni przegrody od strony pomieszczenia nie wystąpi kondensacja pary wodnej.

3. Sprawdzenie możliwości kondensacji pary wodnej wewnątrz przegrody (metoda Fokina)

Dane:

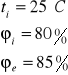
1. Sprawdzenie możliwości kondensacji pary wodnej w przegrodzie dla
   

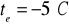
1. Wartość ciśnienia nasyconej pary wodnej
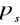
   dla temperatur obliczeniowych

Ciśnienie rzeczywiste w pomieszczeniu

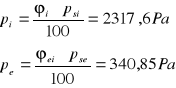
2. Opory dyfuzyjne
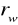
   poszczególnych warstw oraz opór dyfuzyjny całej przegrody

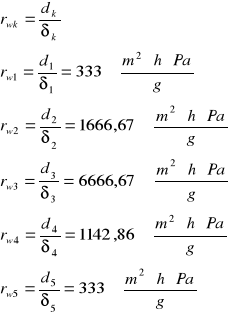
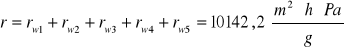
WNIOSEK:

Z wykresu ciśnienia pary wodnej nasyconej ps wynika, że w przegrodzie nastąpi kondensacja pary wodnej.

3. Opór cieplny „R” oraz dyfuzyjny rk części przegrody pomiędzy powierzchnią przegrody od strony pomieszczenia i PMK

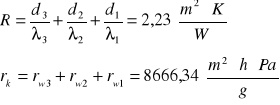
Ciśnienie pk:

Stąd przy temperaturze te=-5°C w przegrodzie wystąpi kondensacja pary wodnej.

3.5. Wyznaczenie temperatury początku kondensacji

• Obliczeniowa wartość temperatury powietrza na zewnątrz
  

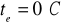
warstwa	ti [^0C]	te [^0C]	RT [m^2*K/W]	Ri [m^2*K/W]	i [^0C]	psi [Pa]
	25	0	2,566	0	25	3169
i	25	0	2,566	0,13	23,7334	2932
1	25	0	2,566	0,148	23,5581	2915
2	25	0	2,566	0,578	19,3687	2254
3	25	0	2,566	2,358	2,0265	705
4	25	0	2,566	2,508	0,56508	640
5	25	0	2,566	2,526	0,38971	630
e	25	0	2,566	2,566	0	611

Ciśnienie rzeczywiste:

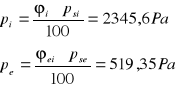
Ciśnienie
:

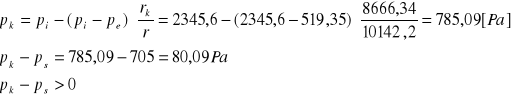
Stąd przy temperaturze te=0°C w przegrodzie wystąpi kondensacja pary wodnej.

• Obliczeniowa wartość temperatury powietrza na zewnątrz
  

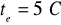
warstwa	ti [^0C]	te [^0C]	RT [m^2*K/W]	Ri [m^2*K/W]	i [^0C]	psi [Pa]
	25	5	2,566	0	25	3169
i	25	5	2,566	0,13	23,9867	2968
1	25	5	2,566	0,148	23,8465	2950
2	25	5	2,566	0,578	20,4949	2413
3	25	5	2,566	2,358	6,6212	978
4	25	5	2,566	2,508	5,45207	896
5	25	5	2,566	2,526	5,31177	890
e	25	5	2,566	2,566	5	872

Ciśnienie rzeczywiste:

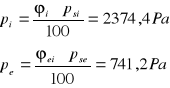
Ciśnienie
:

Stąd przy temperaturze te=5°C w przegrodzie nie wystąpi kondensacja pary wodnej.

Temperatura, przy której rozpoczyna się kondensacja wynosi

Obliczając wartość temperatury powietrza zewnętrznego
przy której w przegrodzie zaczyna się kondensacja otrzymamy temperaturę:

Do dalszych obliczeń przyjęto temperaturę początku kondensacji
. Dla tej temperatury odczytano średnią temperaturę powietrza okresu kondensacji

(I strefa klimatyczna) oraz liczbę dób w ciągu roku „z” o temperaturze
. I tak:

z=139 dni, zatem długość okresu kondensacji:

Średnia temperatura powietrza dla okresu z=139,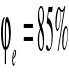
,

warstwa	ti [^0C]	te'' [^0C]	RT [m^2*K/W]	Ri [m^2*K/W]	i [^0C]	psi [Pa]
	25	-0,9	2,566	0	25	3169
i	25	-0,9	2,566	0,13	23,6878	2931
1	25	-0,9	2,566	0,148	23,5062	2897
2	25	-0,9	2,566	0,578	19,1659	2227
3	25	-0,9	2,566	2,358	1,19945	667
4	25	-0,9	2,566	2,508	-0,3146	595
5	25	-0,9	2,566	2,526	-0,4963	587
e	25	-0,9	2,566	2,566	-0,9	567

Ciśnienie rzeczywiste:

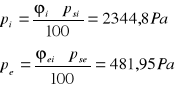
1. Ilość kondensatu w przegrodzie:

Obliczamy ilość kondensatu W
powstającego w przegrodzie w całym okresie kondensacji. Ilość pary wodnej kondensującej się w przegrodzie wynika z różnicy gęstości strumieni dyfuzji pary napływającej i odpływającej ze strefy kondensacji oraz okresu kondensacji.

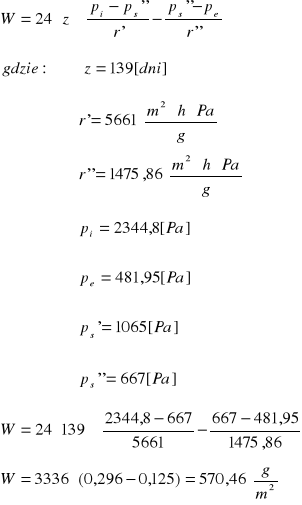
2. Przyrost wilgotności warstwy materiału ΔU[%], w którym występuje kondensacja

• Przyrost wilgotności w cegle pełnej

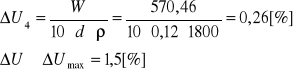
• Przyrost wilgotności w styropianie

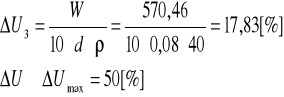
1. Wysychanie wilgotności skondensowanej w przegrodzie budowlanej

• Długość okresu wysychania

• Średnia temperatura powietrza dla okresu wysychania

• Średnia wilgotność względna powietrza

• Ciśnienie cząstkowe pary wodnej w powietrzu na zewnątrz

• Ciśnienie cząsteczkowe pary wodnej w powietrzu w pomieszczeniu

• Temperatura na powierzchni i wewnątrz przegrody

warstwa	ti [^0C]	te'' [^0C]	RT [m^2*K/W]	Ri [m^2*K/W]	i [^0C]	psi [Pa]
	25	12,67	2,566	0	25	3169
i	25	12,67	2,566	0,13	24,3753	3059
1	25	12,67	2,566	0,148	24,2888	3040
2	25	12,67	2,566	0,578	22,2226	2678
3	25	12,67	2,566	2,358	13,6695	1569
4	25	12,67	2,566	2,508	12,9487	1488
5	25	12,67	2,566	2,526	12,8622	1479
e	25	12,67	2,566	2,566	12,67	1460

• Ciśnienie pary wodnej nasyconej w płaszczyźnie kondensacji

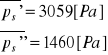
• Średnia wartość ciśnienia pary nasyconej w płaszczyźnie kondensacji w okresie wysychania

• Ilość wilgotności wysychającej w okresie wysychania

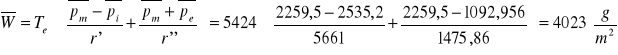
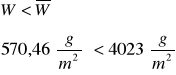
WNIOSKI:

Ilość wilgoci gromadzącej się w przegrodzie w okresie kondensacji jest mniejsza od obliczanej ilości wilgoci, która może wyschnąć w okresie letnim

.

W przegrodzie nie powinno więc nastąpić powiększenie zawilgocenia materiałów z roku na rok, czego konsekwencją mogłoby być nawet naruszenie konstrukcji budynku. Biorąc pod uwagę izolacyjność cieplną przegrody stwierdzam, że przy założeniu, iż dopuszczalna wartość współczynnika przenikania ciepła wynosi
, przegroda nie spełnia wymagań normowych (
). Należy również podkreślić, iż stwierdzono, że na powierzchni przegrody od strony pomieszczenia nie wystąpi kondensacja pary wodnej.

---