przemek

Ćwiczenie nr 7

WYZNACZANIE ENERGII AKTYWACJI PRZEWODNICTWA ELEKTRYCZNEGO DLA NATYWNEGO POLI(3ALKILOTIOFENU) W OBSZARZE DOMIESZKOWANYM I

SAMOISTNYM

Przewodniki dzielimy ze względu na ich właściwości na metale, półprzewodniki i izolatory. W metalach i półprzewodnikach przewodnictwo, jak wspomniano wcześniej ma charakter elektronowy. Izolatorami mogą być zarówno wysokooporowe materiały o przewodnictwie elektronowym jak i jonowym.

W grupie przewodników elektrycznych (pierwiastki, związki nieorganiczne i organiczne), zasadnicza cechą różnicującą je, jest niewystępowanie (metale), lub obecność (półprzewodniki, izolatory) przerwy energetycznej między pasmem walencyjnym a pasmem przewodnictwa Wielkość tej przerwy obok wartości pizewodnictwa elektrycznego pozwala z kolei odróżniać przewodniki od izolatorów. Naogół, uważa się, ze substancje o oporności właściwej rzędu 10¹²-10²² om*cm i wielkości przerwy energii wzbronionych od 4 do 6 eV należą do grupy izolatorów. Typowe półprzewodniki nieorganiczne mają wielkość przerwy energetycznej w obszarze 0-3 eV i wartość przewodnictwa właściwego rzędu 10"¹²- 10² S/cm. Istotnym rozróżnieniem między metalami u półprzewodnikami i izolatorami jest zależność przewodnictwa od temperatury. Dla półprzewodników i izolatorów w przeciwieństwie do metali przewodnictwo elektryczne s rośnie.

Wielkość przerwy energetycznej (szczeliny energetycznej) dla typowych półprzewodników w obszarze samoistnym wyznacza się z zależności uwzględniając, że Eg = 2 E_T.

Równie często wielkość E_g wyznacza się eksperymentalnie z krawędzi widma absorpcji optycznej.

Przyłożenie różnicy potencjałów V do układu w którym istnieje „gaz elektronowy" powoduje powstanie w nim pola elektrycznego o natężeniu E=V/d (d-odleglość), które działa na elektron o ładunku elementarnym e z siłą elektrostatyczną F =-eE. Elektron taki doznaje przyśpieszenia a = f/m_e, w kierunku przeciwnym do pola (uporządkowany ruch ładunków) i osiągałby coraz większe prędkości (ruch jednostajnie przyśpieszony) gdyby nie ddziaływanie z fononami (drgania sieci zrębów atomowych) i domieszkami istniejącym w realnym układzie. Zderzenia elektronu z jonami sieci i domieszkami powoduje gwałtowna utratę prędkości,

Jeśli uwzględnimy, że każdy elektron oderwany od atomu lub przeniesiony z pasma walencyjnego do pasma przewodnictwa pozostawia w nim "dziurę" elektronową, która może poruszać się (w kieirnku przeciwnym niz elektron).

Gdy rozważany układ jest przewodnikiem samoistnym (bez domieszek) to liczba elektronów-..
przeniesionych do pasma przewodnictwa n_c równa jest liczbie dziur w paśmie walencyjnym n_c.

Ruchliwość decyduje o transporcie elektrycznym i jest zależna od mechanizmu rozpraszania nośników ładunków.

Oświadczam, że zapoznałem się z kartami charakterystyk związków wykonywanych w doświadczeniu, i związanymi z nimi zagrożeniami oraz zasadami postępowania w nagłych wypadkach.

Obliczenia:

Dane:

Ogrzewanie			Ochładzanie
Temp ºC	Natężenie nA	A	Temp ºC	Natężenie nA	A
21	5,849	5,849E-09
25	7,122	7,122E-09	25	0,0083	8,3E-12
30	9,356	9,356E-09	30	0,0331	3,31E-11
35	2,891	2,891E-09	35	0,0768	7,68E-11
40	3,206	3,206E-09	40	0,1135	1,14E-10
45	3,888	3,888E-09	45	1,761	1,76E-09
50	5,644	5,644E-09	50	2,126	2,13E-09
55	32,13	3,213E-08	55	2,78	2,78E-09
60	41,56	4,156E-08	60	3,528	3,53E-09
65	54,79	5,479E-08	65	4,386	4,39E-09
70	67,43	6,743E-08	70	5,419	5,42E-09
75	85,13	8,513E-08	75	6,792	6,79E-09
80	106,51	1,0651E-07	80	9,834	9,83E-09
85	134,56	1,3456E-07	85	12,333	1,23E-08
90	167,24	1,6724E-07	90	16,15	1,62E-08
95	215,9	2,159E-07	95	20,14	2,01E-08
100	256,7	2,567E-07	100	24,32	2,43E-08
105	301,5	3,015E-07	105	31,14	3,11E-08
110	359,7	3,597E-07	110	38,99	3,9E-08
115	417,2	4,172E-07	115	48,23	4,82E-08
120	484,6	4,846E-07	120	27,24	2,72E-08
125	537,8	5,378E-07	125	30,72	3,07E-08
130	595,7	5,957E-07	130	36,14	3,61E-08
135	641,7	6,417E-07	135	48,17	4,82E-08
140	693,1	6,931E-07	140	55,36	5,54E-08
145	739,9	7,399E-07	145	62,47	6,25E-08
150	783	0,000000783	150	183,5	1,84E-07
155	829,8	8,298E-07	155	213,3	2,13E-07
160	871,4	8,714E-07	160	243,5	2,44E-07
165	929,8	9,298E-07	165	294,8	2,95E-07
170	971,8	9,718E-07	170	351,4	3,51E-07
175	1034,9	1,0349E-06	175	421,8	4,22E-07
180	1100	0,0000011	180	475	4,75E-07
185	1160,4	1,1604E-06	185	562,9	5,63E-07
190	1233,3	1,2333E-06	190	711,7	7,12E-07
195	1277,5	1,2775E-06	195	832,4	8,32E-07
200	1284	0,000001284	200	982,4	9,82E-07

a) ogrzewanie

Obliczam przewodnictwo właściwe σ ze wzor:

I = σ * S/d * V

σ = SV/dI

Gdzie:

S - powierzchnia elektrody [mm²]

d - grubość pastylki w mm

V - napięcie [15V]

I - natężenie prądu [A]

sigma	ln sigma	1/t
8,61517E-05	-9,3594	0,5
0,000104902	-9,16248	0,25
0,000137807	-8,88965	0,166667
4,25824E-05	-10,0641	0,125
4,72221E-05	-9,96065	0,1
5,72675E-05	-9,76778	0,083333
8,31322E-05	-9,39508	0,071429
0,000473252	-7,65588	0,0625
0,00061215	-7,39853	0,055556
0,000807018	-7,12216	0,05
0,000993197	-6,91458	0,045455
0,001253905	-6,68149	0,041667
0,001568818	-6,45743	0,038462
0,001981975	-6,22366	0,035714
0,002463328	-6,00624	0,033333
0,003180056	-5,75086	0,03125
0,003781011	-5,57776	0,029412
0,004440884	-5,4169	0,027778
0,005298129	-5,2404	0,026316
0,006145064	-5,09211	0,025
0,007137818	-4,94235	0,02381
0,007921417	-4,83819	0,022727
0,008774244	-4,73593	0,021739
0,009451791	-4,66155	0,020833
0,010208877	-4,5845	0,02
0,010898209	-4,51916	0,019231
0,011533041	-4,46254	0,018519
0,012222373	-4,40449	0,017857
0,012835111	-4,35557	0,017241
0,013695303	-4,2907	0,016667
0,014313933	-4,24652	0,016129
0,015243352	-4,18361	0,015625
0,016202229	-4,12261	0,015152
0,017091879	-4,06915	0,014706
0,018165645	-4,00822	0,014286
0,01881668	-3,97301	0,013889
0,01891242	-3,96794	0,013514

Korzystając z równania sporządziłem wykres zależności ln σ = f(1/t). Został on sporządzony dla wartości temp. powyżej 80 ^oC, gdyż w tym zakresie wykres jest prostoliniowy i pozwala na wyznaczenie wartości energii przerwy wzbronionej Eg z relacji Eg = 2*E_T dla przewodnictwa samoistnego.

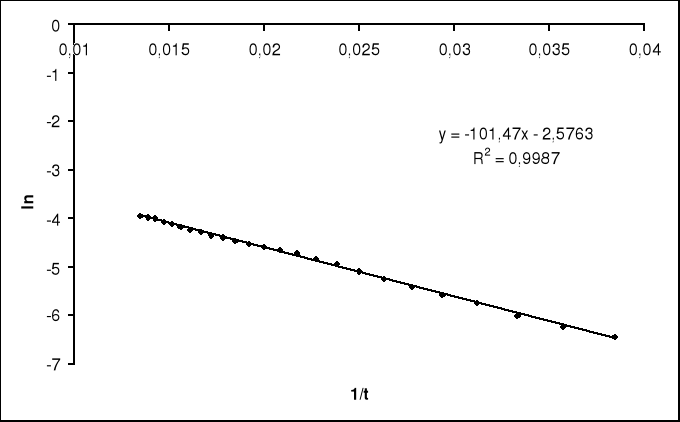
Wyliczam wartość E_T ze wzoru:

tgα = -E_T/k_B

gdzie:

k_B - stała Boltzmana

y = ax + b

ax = -E_T/k_B * 1/T

E_T = a * (-1/T)

gdzie a = -91,634

kB = 8,617*10^-5 eV/K

E_T = 0,008744 eV

b) ochładzanie

Obliczenia wykonuje jak przy ogrzewaniu.

Obliczam przewodnictwo właściwe σ :

sigma	ln sigma	1/t
1,22253E-07	-15,9172	0
4,8754E-07	-14,5339	0,25
1,13121E-06	-13,6922	0,166667
1,67178E-06	-13,3016	0,125
2,59383E-05	-10,5598	0,1
3,13145E-05	-10,3714	0,083333
4,09475E-05	-10,1032	0,071429
5,1965E-05	-9,86494	0,0625
6,46027E-05	-9,64725	0,055556
7,98181E-05	-9,43576	0,05
0,000100041	-9,20993	0,045455
0,000144848	-8,83983	0,041667
0,000181656	-8,61339	0,038462
0,000237878	-8,34375	0,035714
0,000296648	-8,12296	0,033333
0,000358217	-7,93437	0,03125
0,00045867	-7,68718	0,029412
0,000574295	-7,46237	0,027778
0,000710394	-7,24969	0,026316
0,000401226	-7,82099	0,025
0,000452484	-7,70076	0,02381
0,000532317	-7,53827	0,022727
0,00070951	-7,25094	0,021739
0,000815414	-7,11181	0,020833
0,000920139	-6,99099	0,02
0,002702826	-5,91346	0,019231
0,00314176	-5,76297	0,018519
0,003586584	-5,63055	0,017857
0,004342197	-5,43937	0,017241
0,005175876	-5,26375	0,016667
0,006212818	-5,08114	0,016129
0,006996417	-4,96236	0,015625
0,008291123	-4,79257	0,015152
0,010482842	-4,55802	0,014706
0,012260669	-4,40136	0,014286
0,014470064	-4,23567	0,013889

Tak jak w przypadku a, korzystając z równania sporządziłem wykres zależności ln σ = f(1/t). Został on sporządzony dla wartości temp. powyżej 80 ^oC, gdyż w tym zakresie wykres przypomina prebieg prostoliniowy i pozwala na wyznaczenie wartości energii przerwy wzbronionej Eg z relacji Eg = 2*E_T dla przewodnictwa samoistnego.

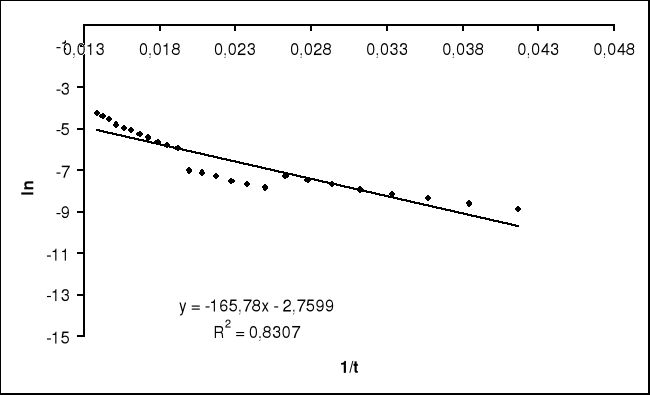
Wyliczam wartość E_T ze wzoru:

E_T = 0,014285 eV

Obliczam wartość energii przerwy wzbronionej:

Eg = 0,028571 eV

Wnioski

Wykres zależności ln σ = f(1/t) składa się z dwóch odcinków (prawie prostoliniowych) rozdzielonych obszarem przejściowym. Odcinek niskotemperaturowy odpowiada sytuacji w której energia aktywacji przewodnictwa związana jest z dominacją efektów ( generacji nośników i transportu ) związanym z domieszkami, które mogą być zjonizowane ( dostarczają wówczas elektronów lub dziur ) lub obojętne ( wpływają tylko na ruchliwość ). Obszar wysokotemperaturowy (przewodnictwo samoistne) związany jest głównie z rozpraszaniem termicznie generowanych nośników w skutek oddziaływania z fononami akustycznymi i optycznymi sieci jonów, i te efekty mają wpływ na wartość energii aktywacji.

Korzystając z tych wiadomości wyznaczyliśmy energie aktywacji E_T oraz energie przerwy wzbudzonej Eg z obszaru wysokotemperaturowego wykresu ( powyżej 80 ^oC).

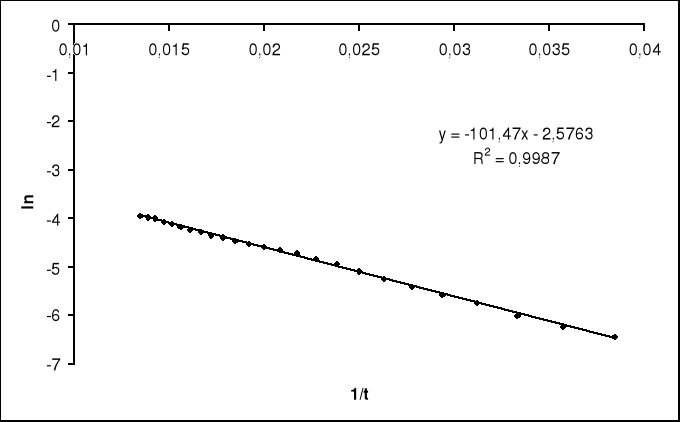
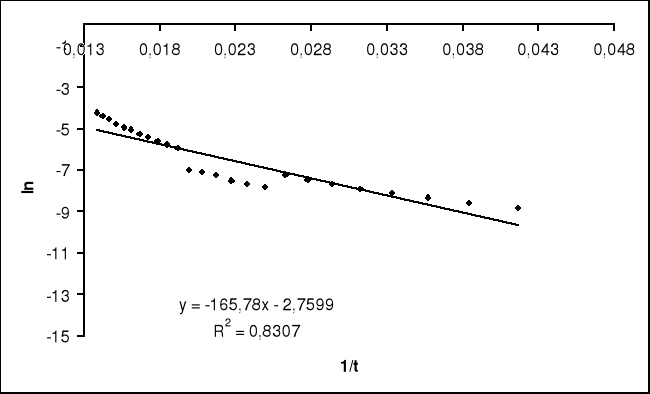
Dla uzyskanych wyników podczas ogrzewania korelacja prostej wynosi R2 = 0,9987 co świadczy o dokładnym wykonaniu pomiarów, zaś dla wyników uzyskanych podczas ochładzania korelacja prostej wynosi R2 = 0,8207, dlatego też wzięto zakres temp. Powyżej 100⁰C dzięki czemu uzyskano lepszą korelację dla linii trędu.

---