Laboratorium
Prądnica tachometryczna
Automatyka i Robotyka sem. III,
grupa 2, sekcja 1
Data odbycia ćwiczenia: 16.12.2009r.
Skład sekcji:
Arkadiusz Gala
Piotr Demski
Robert Nyga
Grzegorz Synowiec
Krzysztof Wierzgacz
Roland Dondera
Adam Partyka
Mikołaj Labus
Mateusz Mikulski
Bartosz Łagosz
1. Wstęp teoretyczny
DAPTA - dwufazowa asynchroniczna prądnica tachometryczna
Prądnica tachometryczna jest urządzeniem, które przetwarza energię mechaniczną na elektryczną, a dokładniej ruch obrotowy na sygnał elektryczny taki jak napięcie lub częstotliwość. Ze względu na efekt pracy prądnice tachometryczne dzieli się na maszyny prądu stałego lub zmiennego. Dla prądu zmiennego wyróżnia się z kolei prądnice indukcyjne oraz synchroniczne. DAPTA to urządzenie asynchroniczne, tzn. nie istnieje żaden związek pomiędzy prędkością z jaką obraca się wirnik a częstotliwością napięcia sinusoidalnie zmiennego, jakie prądnica generuje. Zmiana prędkości wirnika powoduje zmianę wytwarzanego napięcia.
Budowa i zasada działania:
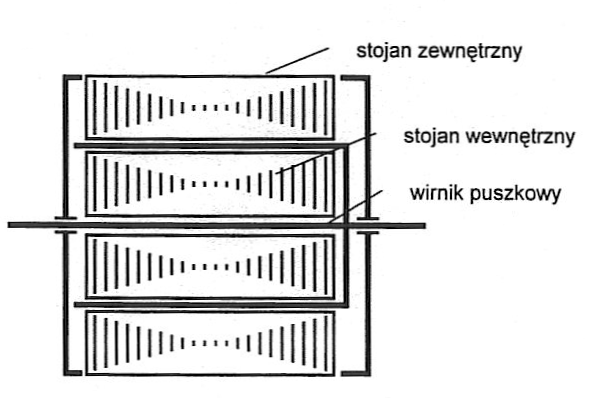
DAPTA składa się wirnika i stojana. Na stojanie znajdują się dwa uzwojenia przesunięte względem siebie o kąt elektryczny . Jedno z nich jest uzwojeniem wzbudzenia, na które podajemy napięcie sinusoidalnie zmienne o stałej częstotliwości i amplitudzie. Z drugiego z nich odbieramy energię elektryczną przetworzoną w maszynie.
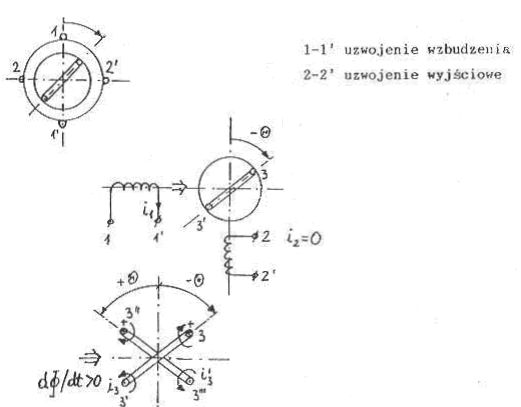
Na uzwojenie wzbudzenia podajemy napięcie sinusoidalnie zmienne. To powoduje przepływ przez nie prądu, co jest z kolei przyczyną powstania zmiennego strumienia magnetycznego w szczelinie maszyny. Skutkiem tego jest pojawienie się w wirniku wirowych prądów transformacji. Jeżeli teraz zaczniemy kręcić wirnikiem to prądy w nim płynące będą spowodowane superpozycją napięcia rotacji i napięcia transformacji. Prądy płynące w wirniku przyczyniają się z kolei do wytwarzania strumienia, który oddziałuje bezpośrednio na uzwojenie wyjściowe maszyny i wymusza w nim napięcie sinusoidalnie zmienne.
Schemat połączeń:
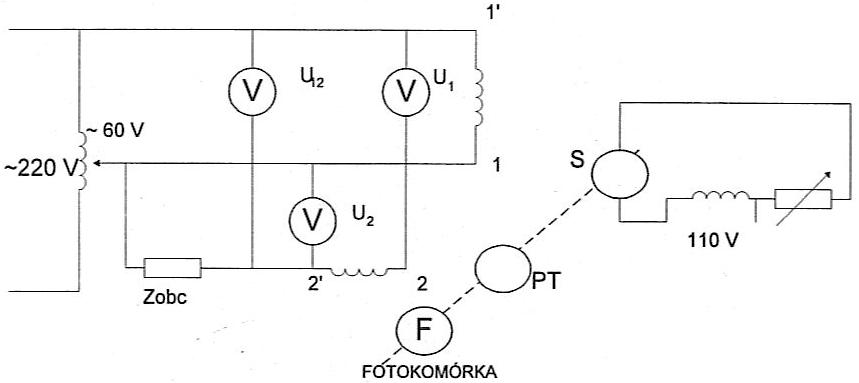
2. Program ćwiczenia
Należało zmierzyć u1,u2,u12 dla 7 różnych prędkości obrotowych ωr. Prądnicę badano przy czterech różnych obciążeniach wskazanych przez prowadzącego, równych 0 kΩ, 6 kΩ, 8 kΩ i 10 kΩ. Z oscyloskopu odczytywano okresy T. Wszystkie potrzebne dane należało wstawiać do tabel pomiarowych.
3. Przedmiot sprawozdania
Na podstawie zebranych pomiarów należało narysować odpowiednie charakterystyki, tj. u2 = f(ωr) , φ = f(ωr). Następnie po wykonaniu odpowiednich obliczeń uzyskano wartości U2i oraz φ 2i, które potrzebne były do narysowania ΔU2 i Δ φ. Wszystkie wykresy oraz obliczenia zostały powtórzone dla wszystkich obciążeń.
4. Tabele pomiarowe
Na następnej stronie znajdują się tabele pomiarowe zawierające wartości zmierzone podczas zajęć.
u1 [V] |
u12 [V] |
u2 [V] |
T [ms] |
R [kΩ] |
58 |
64 |
5 |
3 |
0
|
58 |
68 |
9 |
1,5 |
|
58 |
70 |
12,5 |
1 |
|
58 |
72 |
16 |
0,8 |
|
58 |
76 |
19,5 |
0,6 |
|
58 |
80 |
23 |
0,5 |
|
58 |
84 |
25 |
0,35 |
|
u1 [V] |
u12 [V] |
u2 [V] |
T [ms] |
R [kΩ] |
60 |
64 |
6,5 |
2 |
6
|
60 |
66 |
10,5 |
1,25 |
|
60 |
70 |
14,5 |
0,8 |
|
60 |
72 |
16 |
0,75 |
|
60 |
76 |
19 |
0,6 |
|
60 |
80 |
22,5 |
0,5 |
|
60 |
84 |
24,5 |
0,4 |
|
u1 [V] |
u12 [V] |
u2 [V] |
T [ms] |
R [kΩ] |
60 |
64 |
7 |
2 |
8
|
60 |
68 |
11,5 |
1 |
|
60 |
70 |
15 |
0,75 |
|
60 |
74 |
17 |
0,7 |
|
60 |
76 |
19,5 |
0,6 |
|
60 |
78 |
22 |
0,5 |
|
60 |
82 |
24 |
0,4 |
|
u1 [V] |
u12 [V] |
u2 [V] |
T [ms] |
R [kΩ] |
60 |
64 |
5,5 |
2,5 |
10
|
60 |
66 |
8,5 |
1,5 |
|
60 |
70 |
13 |
1 |
|
60 |
72 |
17 |
0,8 |
|
60 |
76 |
19 |
0,6 |
|
60 |
78 |
20,5 |
0,55 |
|
60 |
82 |
24,5 |
0,4 |
|
5. Obliczenia prędkości kątowej ωr, kąta przesunięcia φ oraz wykreślenie ich charakterystyk
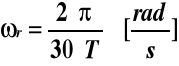
R=0 kΩ |
R=6 kΩ |
R=8 kΩ |
R=10 kΩ |
||||||
u2 [V] |
ωr [rad/s] |
u2 [V] |
ωr [rad/s] |
u2 [V] |
ωr [rad/s] |
u2 [V] |
ωr [rad/s] |
||
5 |
69,81317 |
6,5 |
104,7198 |
7 |
104,7198 |
5,5 |
83,7758 |
||
9 |
139,6263 |
10,5 |
167,5516 |
11,5 |
209,4395 |
8,5 |
139,6263 |
||
12,5 |
209,4395 |
14,5 |
261,7994 |
15 |
279,2527 |
13 |
209,4395 |
||
16 |
261,7994 |
16 |
279,2527 |
17 |
299,1993 |
17 |
261,7994 |
||
19,5 |
349,0659 |
19 |
349,0659 |
19,5 |
349,0659 |
19 |
349,0659 |
||
23 |
418,879 |
22,5 |
418,879 |
22 |
418,879 |
20,5 |
380,7991 |
||
25 |
598,3986 |
24,5 |
523,5988 |
24 |
523,5988 |
24,5 |
523,5988 |
||

R=0 kΩ |
R=6 kΩ |
R=8 kΩ |
R=10 kΩ |
||||||
φ [rad] |
ωr [rad/s] |
φ [rad] |
ωr [rad/s] |
φ [rad] |
ωr [rad/s] |
φ [rad] |
ωr [rad/s] |
||
3,141593 |
69,81317 |
2,191651 |
104,7198 |
2,131926 |
104,7198 |
2,354181 |
83,7758 |
||
3,141593 |
139,6263 |
2,382119 |
167,5516 |
2,273385 |
209,4395 |
2,305467 |
139,6263 |
||
2,82904 |
209,4395 |
2,247585 |
261,7994 |
2,21083 |
279,2527 |
2,381831 |
209,4395 |
||
2,573024 |
261,7994 |
2,334591 |
279,2527 |
2,462179 |
299,1993 |
2,258551 |
261,7994 |
||
2,686476 |
349,0659 |
2,491541 |
349,0659 |
2,445595 |
349,0659 |
2,491541 |
349,0659 |
||
2,792417 |
418,879 |
2,585903 |
418,879 |
2,430387 |
418,879 |
2,566097 |
380,7991 |
||
3,141593 |
598,3986 |
2,901616 |
523,5988 |
2,656694 |
523,5988 |
2,602975 |
523,5988 |
||
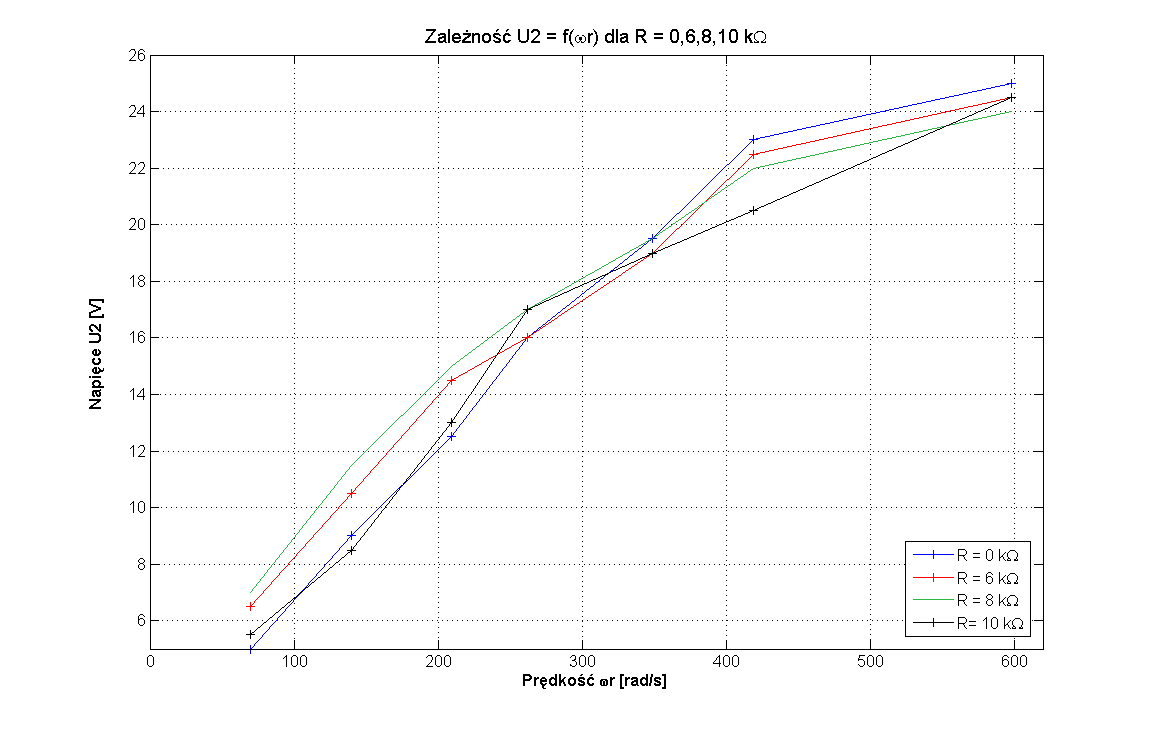
Charakterystyki u2 = f(ωr)
Charakterystyki φ = f(ωr)
6. Obliczenia napięcia idealnego U2i, kąta φ2i oraz wykreślenie charakterystyk Δu2 oraz Δφ2
W celu wyznaczenia charakterystyk ![]()
oraz wartości U2i korzystamy z zależności:
gdzie M-ilość pomiarów, M=7
Otrzymujemy układ trzech równań niejednorodnych z trzema niewiadomymi c1,c2,c3. Rozwiązując ten układ uzyskujemy następujące wyniki:
Dla R= 0 kΩ
C1= 16410
Dla R= 6 kΩ
C1= 18700
Dla R=8 kΩ
C1= 20251
Dla R=10 kΩ
C1= 10634
Następnie korzystamy z zależności:
R=0 kΩ |
R=6 kΩ |
R=8 kΩ |
R=10 kΩ |
||||||
U2i |
Δu2 |
U2i |
Δu2 |
U2i |
Δu2 |
U2i |
Δu2 |
||
0,255258 |
4,744742 |
0,335999 |
6,164001 |
0,310265 |
6,689735 |
0,472687 |
5,027314 |
||
0,510517 |
8,489483 |
0,537599 |
9,962401 |
0,620531 |
10,87947 |
0,787811 |
7,712189 |
||
0,765775 |
11,73422 |
0,839998 |
13,66 |
0,827374 |
14,17263 |
1,181716 |
11,81828 |
||
0,957219 |
15,04278 |
0,895998 |
15,104 |
0,886473 |
16,11353 |
1,477145 |
15,52285 |
||
1,276292 |
18,22371 |
1,119997 |
17,88 |
1,034218 |
18,46578 |
1,969527 |
17,03047 |
||
1,53155 |
21,46845 |
1,343997 |
21,156 |
1,241062 |
20,75894 |
2,148575 |
18,35142 |
||
2,187929 |
22,81207 |
1,679996 |
22,82 |
1,551327 |
22,44867 |
2,954291 |
21,54571 |
||
Natomiast charakterystyka ![]()
oraz wartości ![]()
:
![]()
=0 =>
![]()
=0 =>
![]()
=0 =>
![]()
=0 =>
Tym razem otrzymujemy jednorodny układ równań liniowych. Wyznaczamy ![]()
.
Otrzymujemy wartości:
Dla R= 0 kΩ
d3= 6,5423
Dla R= 6 kΩ
d3= 4,0854
Dla R= 8 kΩ
d3= 4,0673
Dla R= 10 kΩ
d3= 4,0411
Następnie korzystamy z zależności (podstawiamy d1=1):
R=0 kΩ |
R=6 kΩ |
R=8 kΩ |
R=10 kΩ |
||||||
φ 2i |
Δ φ |
φ 2i |
Δ φ |
φ 2i |
Δ φ |
φ 2i |
Δ φ |
||
-1,722 |
4,861592654 |
-1,811 |
4,002651272 |
-1,813 |
3,944925855 |
-1,815 |
4,169181313 |
||
|
4,861592654 |
|
4,193118842 |
|
4,086385261 |
|
4,120467435 |
||
|
4,549039887 |
|
4,058585459 |
|
4,023829716 |
|
4,196830721 |
||
|
4,293023816 |
|
4,145590546 |
|
4,275178842 |
|
4,073551054 |
||
|
4,406475526 |
|
4,302541156 |
|
4,258595145 |
|
4,306541156 |
||
|
4,512417328 |
|
4,396903393 |
|
4,243387488 |
|
4,381097218 |
||
|
4,861592654 |
|
4,712616056 |
|
4,469694062 |
|
4,417974594 |
||
Charakterystyki Δu2 = f(ωr)
Charakterystyki Δφ = f(ωr)
7. Podsumowanie i wnioski
Na podstawie wykreślonych charakterystyk zależności u2 = f(ωr) dla zadanych kolejno czterech obciążeń wynoszących kolejno: R = 0; 6; 8 oraz 10 kΩ, jednoznacznie stwierdzić można, iż wszystkie z nich są w przybliżeniu liniowe. Dodatkowo obserwuje się nieznaczne zmniejszenie kąta nachylenia tychże charakterystyk do osi OX, wraz ze wzrostem obciążenia. Wartości prędkości ωr dla kolejnych obciążeń są do siebie bardzo zbliżone.
Wykresy zależności φ = f(ωr) nie są natomiast jawnie liniowe, jednakże łatwo dają się zaproksymować. Po wykonaniu takiej operacji okaże się, że zależność dla R = 0 kΩ jest w praktyce stała - w niedużym stopniu zmienia się pod wpływem wzrostu prędkości obrotowej ωr. Pozostałe trzy charakterystyki zachowują się podobnie do zależności u2 = f(ωr), czyli wraz ze wzrostem obciążenia, proste aproksymujące zmniejszają swój kąt nachylenia do osi OX. Liczbowo natomiast wartości kąta φ zmniejszają się stopniowo wraz ze wzrostem obciążenia.
Wykresy charakterystyk ΔU2 = f(ωr) mają dokładnie taki sam kształt dla poszczególnych obciążeń, jak odpowiadające im zależności napięcia u2. Są one jedynie przesunięte względem nich o wartość napięcia idealnego U2i. Jedynym wartym zauważenia faktem, jest „oddalanie” się wykresów u2 oraz ΔU2 wraz ze wzrostem prędkości ωr. Jednakże różnice pomiędzy wartościami zmian napięcia ΔU2, dla wzrastających wielkości obciążeń, są pomijalnie małe.
Wykresy charakterystyk Δφ zachowują się podobnie - także mają dokładnie taki sam kształt co zależności φ i są przesunięte względem nich tym razem o wartość φ idealne.
Wszystkie wykonane pomiary są obarczone oczywiście niepewnościami, które wynikały zarówno z jakości sprzętu do wykonywania pomiarów, jak i błędów odczytu ze skali czy też ekranu oscyloskopu. Dodatkowym czynnikiem były także pewne minimalne wahania napięć, które występowały podczas całej operacji zdejmowania pomiarów.
![]()
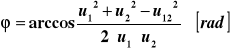
![]()
![]()
![]()
![]()
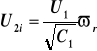
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
swps gr3, Automatyka i Robotyka, Semestr III, Elektrotechnika i Elektromechanika, Gotowce, Elektrome
EiE 20lab 2014.01.2010, Automatyka i Robotyka, Semestr III, Elektrotechnika i Elektromechanika, Goto
SPRAWKO 4 EiE nasze, Automatyka i Robotyka, Semestr III, Elektrotechnika i Elektromechanika, Gotowce
BD Lesiu, Automatyka i Robotyka, Semestr III, Bazy Danych, Gotowce
bdsciaga, Automatyka i Robotyka, Semestr III, Bazy Danych, Gotowce
Mechanika - opracowanie, Automatyka i Robotyka, Semestr III, Mechanika, Gotowce, Mechanika, Mechanik
sprawko moo1, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Optymalizacji, Gotowce, labki
sprawko nowe, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Optymalizacji, Gotowce, labki
sprawozdanie-MaciejPawnukTomaszImiołek, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Opty
GR D, Automatyka i Robotyka, Semestr III, Bazy danych
sciaga a, Automatyka i Robotyka, Semestr III, Bazy danych
sprawko powell, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Optymalizacji, Gotowce, labk
sprawko-6, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Optymalizacji, Laborki, lab6, got
Zestaw C++-zaliczenie wcze, Automatyka i Robotyka, Semestr III, Języki programowania
więcej podobnych podstron