Badanie aktywacji termicznej reakcji chemicznej
Szybkość reakcji chemicznych zależy od wielu czynników takich, jak temperatura, ciśnienie oraz właściwości ośrodka, w którym zachodzi reakcja. Arrhenius sformułował równanie opisujące zależność stałej szybkości reakcji od temperatury:
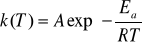
(1)
gdzie: R - stała gazowa
Ea - energia aktywacji
A - czynnik przedwykładniczy zwany współczynnikiem Arrheniusa
Zgodnie z powyższym równaniem stała szybkości k szybko zwiększa się ze wzrostem temperatury T. Im większa energia aktywacji Ea, tym mniejsza jest stała szybkości k, lecz jednocześnie tym większy jest jej wzrost ze wzrostem temperatury. W przypadku reakcji elementarnych energia aktywacji określa minimalną energię, jaką muszą mieć cząsteczki, aby mogły przereagować. Dla reakcji złożonych energia aktywacji nie ma prostego znaczenia fizycznego i zależy od energii aktywacji poszczególnych etapów.
Z równania Arrheniusa można wyznaczyć energię aktywacji wówczas, gdy znana jest stała szybkości reakcji k dla dwóch różnych temperatur T1 T2. Z danych eksperymentalnych wynika, że współczynnik Arrheniusa A może zależeć od temperatury, co przewiduje teoria stanu przejściowego.
Energia reagujących cząsteczek zależy od ich odległości i wzajemnej orientacji, które zmieniają się w trakcie reakcji. W teorii stanu przejściowego elementarny etap reakcji jest przedstawiony jako przejście substratów poprzez stan przejściowy do produktów.
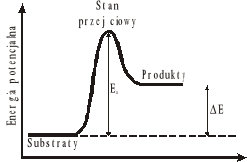
Teoria ta prowadzi do tzw. równania Eyringa, które określa zależność stałej szybkości k od temperatury T, entalpii aktywacji i entropii aktywacji S#:
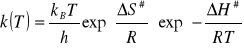
(2)
gdzie: h - stała Plancka
kB - stała Boltzmana
Z równania Eyringa można wyznaczyć energię aktywacji wówczas, gdy znana jest stała szybkości reakcji dla dwóch różnych temperatur.
Celem naszego ćwiczenia jest na podstawie wyznaczonych stałych reakcji k w różnych temperaturach określenie współczynnika Arrheniusa A oraz energii aktywacji Ea w równaniu (1), oraz S# i H# aktywacji w równaniu (2) co z kolei pozwoli nam obliczyć G# reakcji hydrolizy bromku t-butylu w roztworze wodno-etanolowym.
Opracowanie wyników
Włączono termostat i ustawiono temperaturę 25°Cnapełniono zlewkę 50cm3 80% roztworu butanolu w wodzie, napełnione naczynie pomiarowe umieszczono w termostacie i włożono do niego elektrodę pomiarową. Po włączeniu konduktometru i odczekaniu 10 minut odczytano wartości konduktancji dla roztworu - Lwe. Następnie dodano do roztworu 0,5cm3 r-ru bromku t-butylu i rozpoczęto pomiar czasu; co minutę odczytywano przewodnictwo elektrolityczne mieszaniny reakcyjnej. Pomiary prowadzono aż do ustabilizowania się jej wartości.
Taki sam przebieg ćwiczenia wykonano dla tej samej reakcji biegnącej w temperaturze 30°C
Czas |
Konduktancja |
|||
|
T1 = 25°C |
T2 = 30°C |
||
|
LMR[ၭS] |
L[ၭS] |
LMR[ၭS] |
L[ၭS] |
0 |
LWE = 29,7 |
0 |
LWE = 35 |
0 |
1 |
57,6 |
22,34 |
64 |
73,4 |
2 |
90,2 |
52,44 |
78 |
186,9 |
3 |
140 |
84,84 |
115 |
258,9 |
4 |
260 |
112,74 |
165 |
313,9 |
5 |
370 |
140,94 |
205 |
353,9 |
6 |
560 |
185,84 |
285 |
382,9 |
7 |
670 |
214,84 |
335 |
416,9 |
8 |
750 |
244,84 |
360 |
460,9 |
9 |
850 |
270,84 |
435 |
461,9 |
10 |
950 |
289,84 |
490 |
497,9 |
11 |
1050 |
313,84 |
560 |
557,9 |
12 |
1100 |
333,84 |
700 |
635,9 |
13 |
1150 |
351,84 |
885 |
716,9 |
14 |
1200 |
373,84 |
1150 |
815,9 |
15 |
1250 |
405,84 |
1350 |
917,9 |
16 |
1300 |
443,84 |
1450 |
1019,9 |
17 |
1350 |
482,84 |
1550 |
1121,9 |
18 |
1400 |
486,84 |
1850 |
1205,9 |
19 |
1450 |
537,84 |
1900 |
1298,9 |
20 |
1500 |
657,84 |
2050 |
1373,9 |
21 |
1550 |
732,84 |
2200 |
1454,9 |
22 |
1570 |
801,84 |
2350 |
1701,9 |
23 |
1580 |
870,84 |
2400 |
1791,9 |
24 |
1580 |
939,84 |
2700 |
1881,9 |
25 |
1580 |
1011,84 |
2750 |
1941,9 |
26 |
1590 |
1065,84 |
2900 |
2031,9 |
27 |
1600 |
1119,84 |
2950 |
2101,9 |
28 |
1650 |
1176,84 |
2220 |
2201,9 |
29 |
1700 |
1275,84 |
2290 |
2271,9 |
30 |
1720 |
1314,84 |
2380 |
2361,9 |
31 |
1780 |
1371,84 |
2440 |
2421,9 |
32 |
1850 |
1422,84 |
2500 |
2481,9 |
33 |
1890 |
1467,84 |
2590 |
2571,9 |
34 |
1940 |
1684,84 |
2670 |
2651,9 |
35 |
1960 |
1714,84 |
2700 |
2681,9 |
36 |
1990 |
1754,84 |
2760 |
2741,9 |
37 |
2060 |
1804,84 |
2810 |
2791,9 |
38 |
2100 |
1864,84 |
2870 |
2851,9 |
39 |
1900 |
1894,84 |
2910 |
2891,9 |
40 |
1940 |
1934,84 |
2980 |
2961,9 |
41 |
1980 |
1974,84 |
3010 |
2991,9 |
42 |
2010 |
2004,84 |
3080 |
3061,9 |
43 |
2060 |
2054,84 |
3110 |
3091,9 |
44 |
2100 |
2094,84 |
3160 |
3141,9 |
gdzie: L = LMR - LWR
Na podstawie pomiarów sporządzamy dwa wykresy zależności L1 = f(L2) i z wykresów odczytujemy współczynnik kierunkowy prostej C.
gdzie: L1 - konduktancja w pierwszej minucie
L2 - konduktancja w kolejnej minucie
C - współczynnik kierunkowy prostej L1 = f (L2), przy czym:
![]()
c0 - stężenie początkowe substratu;
x1, x2 - zmiana stężenia odpowiednio w 1 i 2 minucie
Z wykresów odczytujemy wartości stałej C:
a) dla T1 = 298,15 K C = 1,0129
b) dla T2 = 303,15 K C = 1,0398
Obliczamy stałe szybkości reakcji k1, k2:
Reakcja jest pierwszego rzędu, wzór na stałą k ma następującą postać:
![]()
![]()
a) dla T1 = 298,15 K ![]()
k1 = 0,0128 1/min.
b) dla T2 = 303,15 K ![]()
k2 = 0,0390 1/min.
Obliczamy entalpię tworzenia kompleksu aktywnego ΔH#:
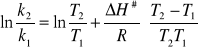
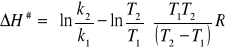
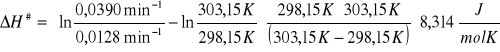
ΔH# = 164 942 J/mol
Obliczamy entropię tworzenia kompleksu aktywnego ΔS#:
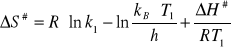
W celu uzgodnienia jednostek wykonuję następującą operację:
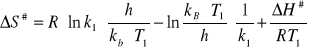
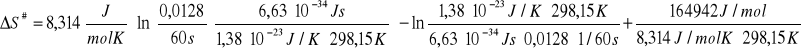
ΔS# = -77,13 J/mol∙K
Sporządzamy wykres zależności stałej szybkości w funkcji temperatury lnk = f (1/T)
![]()
zatem współczynnik kierunkowy dla powyższej prostej wynosi: -19885 [K]
![]()
![]()
![]()
ΔH# = 165 324 J/mol
Obliczamy energię aktywacji:
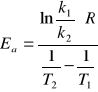

Ea = 167 442 J/mol
Obliczamy współczynnik przedwykładniczy Arrheniusa:
![]()
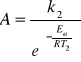

A = 2,76∙1027 min-1
Wnioski
Na podstawie uzyskanych wyników możemy zauważyć, że ze wzrostem temperatury wzrasta szybkość reakcji - stała szybkości dla temperatury wyższej ma większą wartość. Otrzymano następujące stałe szybkości reakcji:
dla T1 = 298,15 K k1 = 0,0363 min-1
dla T2 = 303,15 K k2 = 0,0488 min-1
W trakcie obliczeń otrzymałyśmy następujące wartości entalpii aktywacji:
ΔH# = 164 942 J/mol
ΔH# = 165 324 J/mol - obliczona na podstawie wykresu
Entalpia związana jest z energią tworzenia i rozrywania wiązań podczas reakcji, czyli podczas tworzenia się nowego wiązania do układu została wydzielona energia (część została zużyta na rozerwanie wiązań w substratach, a część została wydzielona do otoczenia). Wartość entalpii uzyskana na podstawie wykresu ln k = f (1/T) jest nieco większa od obliczonej. Ponieważ jednak wykres został wykonany tylko na podstawie dwóch punktów (tylko dla dwóch temperatur), więc cechuje go duża niedokładność.
Na podstawie entropii aktywacji określono cząsteczkowość reakcji. Jest to reakcja jednocząsteczkowa, czyli w etapie o maksymalnej energii bierze udział jedna cząsteczka (zgadza się to z rzeczywistym mechanizmem badanej reakcji, gdyż najwolniejszym etapem jest tu rozpad bromku t-butylu).
Na wartość entalpii i entropii aktywacji mogły mieć wpływ różne czynniki: np. zawada przestrzenna, która powoduje wzrost entalpii aktywacji i jednoczesne zmniejszenie wartości entropii aktywacji; solwatacja stanu przejściowego powoduje zmniejszenie wartości entalpii i entropii, a także polarność substratów (im bardziej polarny związek i im więcej cząstek tworzy ten stan przejściowy tym mniejsza entropia) i budowa stanu przejściowego.
2
Wyszukiwarka
Podobne podstrony:
6, semestr 4, chemia fizyczna, sprawka laborki, 6.11
1.11badanie aktywacji reakcji 6, semestr 4, chemia fizyczna, sprawka laborki, 6.11
10.6 poprawione, semestr 4, chemia fizyczna, sprawka laborki, 10.6
spr 8.5 obliczenia1, semestr 4, chemia fizyczna, sprawka laborki, 8.5
Wyznaczanie 10.6L, semestr 4, chemia fizyczna, sprawka laborki, 10.6
10.1, semestr 4, chemia fizyczna, sprawka laborki, 10.1
8.5 wykres, semestr 4, chemia fizyczna, sprawka laborki, 8.5
10.6 poprawione, semestr 4, chemia fizyczna, sprawka laborki, 10.6
spr 8.5 obliczenia1, semestr 4, chemia fizyczna, sprawka laborki, 8.5
28fizyczna, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizyc
sekuła, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizyczna,
zawiejski, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizycz
więcej podobnych podstron