PRACOWNIA ZAKŁADU FIZYKI PL
		Grupa
Data wykonania ćwiczenia:	Numer ćwiczenia:	Temat ćwiczenia: Wyznaczanie stałej balistycznej galwanometru balistycznego.
Zaliczenie:	Ocena:	Data:	Podpis:

1. Tabela pomiarów

L.p.	C [F]	U0 [V]	q [C]	n [dz]	Sb [C/dz]
1	4 * 10^-6	10	40*10^-6	4700	8,51*10^-9
2							4800	8,33*10^-9
3							4800	8,33*10^-9
4							4700	8,51*10^-9
5							4800	8,33*10^-9
6							4800	8,33*10^-9
7							4700	8,51*10^-9
8							4800	8,33*10^-9
9							4900	8,16*10^-9
10							4800	8,33*10^-9
11							4800	8,33*10^-9
12							4900	8,16*10^-9
13							4800	8,33*10^-9
				Σn=62300 n≈4800	ΣSb=108,49*10^-9 Sbśr=8,34*10^-9

2. Obliczenia







3. Krótka teoria

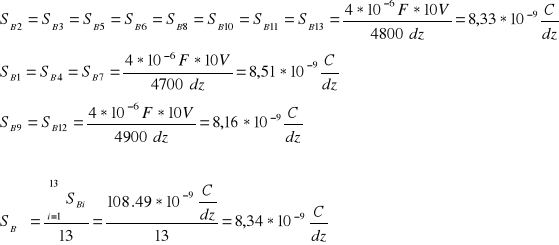
Galwanometr balistyczny jest odmianą galwanometru magnetoelektrycznego o dużym momencie bezwładności ramki (uzyskanym np. przez doczepienie do ramki dodatkowego obciążenia).dzięki temu okres T_o drgań swobodnych ramki galwanometru balistycznego jest stosunkowo duży w porównaniu z czasem t trwania impulsu prądu. Galwanometr balistyczny jest stosowany do pomiaru

małych ładunków elektrycznych , przepływających w obwodzie w czasie krótszym niż okres drgań własnych ramki galwanometru.

4. Schemat ćwiczenia i opis wykonania

Celem ćwiczenia jest zyznaczenie stałej balistycznej dla badanego galwanometru.

W celu wyznaczenia stałej balistycznej wykorzystuję układ pomiarowy przedstawiony na poniższym schemacie:




Prąd stały z zasilacza doprowadza się przez dzielnik napięcia do kondensatora o znanej pojemności C. Jeżeli przełącznik K jest ustawiony w położeniu 1, kondensator zostaje naładowany do napięcia U₀. Po energicznym przełączeniu w położenie 2, naładowany wcześniej kondensator rozładowuje się przez galwanometr balistyczny, wprawiając w ruch jego ramkę. Stałą balistyczną obliczamy ze wzoru:




C - pojemność kondensatora [C]=1F=


U_o- napięcie elektryczne [U]=1V=


n- liczba działek

5. Opracowanie wyników pomiarów

1. Błędy przypadkowe - metoda Gaussa

N≥10

L.p.	C [F]	U0 [V]	n [dz]	rn= n -n[]	r^2n=(n - n)^2[ ]
1	4 * 10^-6	10	4700	-100	0,5*10^4
2					4800	0	0
3					4800	0	0
4					4700	-100	0,5*10^4
5					4800	0	0
6					4800	0	0
7					4700	-100	0,5*10^4
8					4800	0	0
9					4900	100	10^4
10					4800	0	0
11					4800	0	0
12					4900 4800	100	10^4
13
			Σn=62300 n≈4800		Σrn^2=3,5*10^4

Średni błąd kwadratowy pojedynczego pomiaru (odchylenie standardowe)





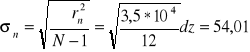
Dla wszystkich pomiarów spełniony jest warunek:

r_n < σ_n

Błędy grube nie występują - pomiary wykonane prawidłowo

Średni błąd kwadratowy średniej arytmetycznej




Średni błąd kwadratowy pomiaru pośredniego







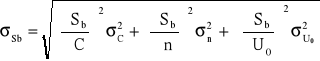
c=const ,


U₀=const ,





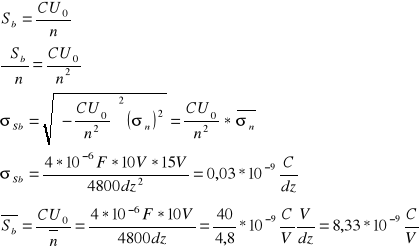
Wynik pomiaru tej wielkości możemy zapisać następująco:

- Przy kryterium jednosigmowym




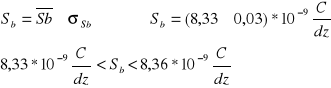
co oznacza, że w tym przedziale można z prawdopodobieństwem p=68,3% oczekiwać wartości rzeczywistej S_b







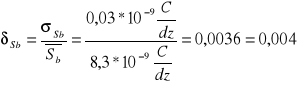
Błąd przeciętny




Błąd prawdopodobny




• Przy kryterium trzysigmowym (większa pewność wyniku)




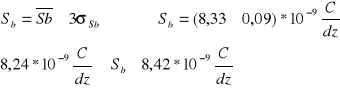
co oznacza, że w tym przedziale można z prawdopodobieństwem p=99,7% oczekiwać wartości rzeczywistej S_b

Błąd względny maksymalny - metoda różniczkowa uproszczona




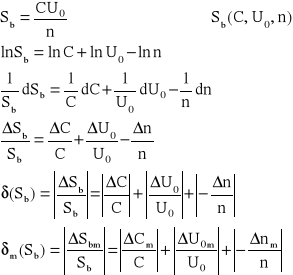
ΔU_{o m}=ΔU_o'+ΔU_o''

Δ U_o' -błąd bezwzględny pomiaru napięcia wynikający z klasy niedokładności miernika


ΔU_o'' - błąd bezwzględny pomiaru napięcia wynikający z niedokładności odczytu




Woltomierz

zakres - 15V

klasa - 0,5

liczba działek - 30


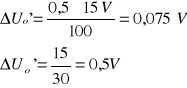
ΔU_{o max} =0,075+0,5=0,575V

Kondensator




Galwanometr

Δn _max=Δn'+Δn''

Δn_max - błąd pomiaru wychylenia związany z niedokładnością skali galwanometru










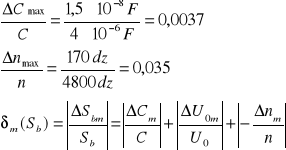
δ_m(S_b)=0,0575+0,0037+0,035 = 0,0962

δ_m(S_b)=9,62%

1

1

---