1.Funkcje wielu zmiennych.

Def. Zmienna z obszarem zmienności (Z) nazywa się funkcją zmiennych niezależnych x i y w obszarze M jeśli każdej parze (x,y) ich wartości z M przyporządkowane jest wg. Pewnej reguły jedna określona wartość z (Z). Same zmienne x i y nazywają się argumentami funkcji z. Zależność funkcyjną oznaczamy z=f(x,y)

Np. z=xy; z=x²y-4y+1...

Granice. Def. Załóżmy, że funkcja n zmiennych u=f(x1,x2...xn) jest określona w pewnym zbiorze punktu D, który ma punkt skupienia M0(a1,a2...an). Liczba A jest granicą funkcji j.w. gdy zmienne x1,x2...xn dążą odpowiednio do a1,a2...an. Jeśli dla każdej z góry zadanej >0 można znaleźć taką δ>0 że |f(x1..xn) - A|< jeśli tylko |x1-a1|<δ, |x2-a2|<δ...

Def2. Liczba a nazywa się granicą funkcji u=f(M) gdy M dąży do M0. Jeśli dla każdej >0 istnieje taka δ>0,że | f(M) - A|< jeśli tylko MM₀ <δ.

2.Pochodne cząstkowe, różniczkowalność funkcji wielu zmiennych.

Niech w pewnym obszarze D przestrzeni n wymiarowej będzie dana funkcja u=f(x1,x1...xn)

Weźmiemy jakikolwiek wewnętrzny punkt Mo(x₁⁰,x₂⁰...x_n⁰). Jeśli ustalimy teraz wartości począwszy od 2 i będziemy zmieniać tylko x1, to funkcja będzie w otoczeniu punktu x₁⁰ funkcją jednej zmiennej x1.

Obliczmy pochodną tej funkcji w p. x₁⁰. Nadajmy tej wartości przyrost x1, wówczas funkcja uzyska przyrost u=f(x₁⁰+x1,x₂⁰+x1...x_n⁰+x1) - f(x₁⁰,x₂⁰...x_n⁰). Zgodnie z samą definicją pochodnej jest ona równa: lim (x1-0) x1u / x1 =

lim (x1-0) f(x₁⁰+x1,x₂⁰+x1...x_n⁰+x1) - f(x₁⁰,x₂⁰...x_n⁰) / x1

Pochodna ta w przypadku istnienia nazywa się pochodną cząstkową funkcji f(x₁⁰,x₂⁰...x_n⁰)

Względem x1 w punkcie Mo. Oznacza się ją: u/x1

Rózniczkowalność: Jeśli wychodząc z wartości x1=x₁⁰,x2=x₂⁰...xn=x_n⁰nadać wszystkim n zmiennym przyrosty x1, x2, ...xn to sama funkcja u=f(x1,x2...xn) dozna przyrostu, który oznaczmy przez u=f(x₁⁰+x1,x₂⁰+x1...x_n⁰+x1) - f(x₁⁰,x₂⁰...x_n⁰).

Def1. Funkcja u=f(x1,x2...xn) nazywa się różniczkowalną w pewnym punkcie M0(x₁⁰,x₂⁰...x_n⁰) jeśli jej przyrost zupełny w tym punkcie może być przedstawiony w postaci:

u= A1x1+A2x2+....Anxn+1x1+...+nxn (1)

gdzie A1, A2, An są stałymi niezależnymi od x1,x2...xn, a 1,2,...n są wielkościami zależnymi od x1,x2...xn i dążącymi wraz z nimi do 0.

Def2. Funkcja u=f(x1,x2...xn) ) nazywa się różniczkowalną w pewnym punkcie M0(x₁⁰,x₂⁰...x_n⁰) jeśli jej przyrost zupełny w tym punkcie może być przedstawiony w postaci:

u= A1x1+A2x2+....Anxn+ +ρ (2)

gdzie: ρ=
, gdzie A1, A2, An są stałymi niezależnymi od x1,x2...xn, a granica : lim (ρ-0)=0

TW. Jeśli funkcja u=f(x1,x2...xn) jest różniczkowalna w punkcie M0(x₁⁰,x₂⁰...x_n⁰) to w tym punkcie istnieją pochodne cząstkowe względem wszystkich argumentów, przy czym u/xi=Ai, i= 1,2,...,n Istnienie pochodnych cząstkowych jeszcze nie pociąga za sobą różniczkowalności funkcji. Trzeba mieć dodatkowe warunki aby ta funkcja była różniczkowalna.

TW. Jeśli pochodne cząstkowe fx'(x,y,z), fy'(x,y,z), fz'(x,y,z) istnieją nie tylko w punkcie (x₀, y₀, z₀) lecz także w pewnym jej otoczeniu i oprócz tego są w tym punkcie ciągłe jako funkcje trzech zmiennych to funkcja u=f(x,y,z)jest różniczkowalna w tym punkcie czyli zachodzi równość 1 lub2.

3. Funkcja złożona wielu zmiennych, pochodna funkcji złożonej.

Niech będzie dana u=f(x1,x2...xn) określona w obszarze D przy czym każda ze zmiennych (x1,x2...xn) jest z kolei funkcją zmiennych x1=1(t1,t2...tm), x2=2(t1,t2...tm), xn=1(t1,t2...tm), Podstawiając wartości x1,x2...xn do funkcji f otrzymujemy: u=f(1(t1,t2...tm), 2(t1,t2...tm), 1(t1,t2...tm))

Załóżmy że funkcja u jest różniczkowalna w punkcie M0(x₁⁰,x₂⁰...x_n⁰) i że wszystkie funkcje 1,2...n też są różniczkowalne w punkcie Po przestrzeni m wymiarowej Po=(t₁⁰,t₂⁰,...,t_m⁰) przy czym wartości x_i⁰=i(t₁⁰,t₂⁰,...,t_m⁰).

Można wówczas udowodnić istnienie pochodnych funkcji u względem t1, t2,...tn, oraz obliczyć te pochodne.

u/x1=u/x1*x1/t1+u/x2*x2/t1+u/xn*xn/t1

u/t2=u/x1*x1/t2+1u/x2*x2/t2+u/xn*xn/t2

u/tm=u/x1*x1/tm+1u/x2*x2/tm+u/xn*xn/tm

Jeśli x1=1(t), x2=2(t), ...xn=n(t)

To: u/t=u/x1*x1/t+u/x2*x2/t+...u/xn*xn/t

Niech funkcja u=f(x1,x2...xn) będzie różniczkowalna w Mo(x₁⁰,x₂⁰...x_n⁰) a więc jej przyrost zupełny może być przedstawiony w postaci (1) lub (2). Liniowa część tego przyrostu nazywamy różniczką zupełną funkcji u i oznaczamy symbolem du lub df(x₁⁰,x₂⁰...x_n⁰).

Du= A1x1+A2x2+....Anxn

Jeśli wszystkie współczynniki A1,A2,…An= 0to umówimy się definiować różniczkę przez ten sam wzór a więc du=0

Korzystając z twierdzenia wg. Którego Ai=u/xi możemy wzór na różniczkę przepisać w postaci:

du=u/x1*dx1+u/x2*dx2+...u/xn*dxn

4.Pochodna kierunkowa.

Pochodne cząstkowe funkcji =f(x,y,z)=f(M) względem x,y,z wyrażają prędkość zmiany funkcji w kierunku osi współrzędnych.

Niech f(M) będzie określona w pewnym obszarze otwartym przestrzeni trójwymiarowej. Rozpatrzmy dowolny punkt tego przedziału Mo(x0,y0,z0) oraz dowolną prostą skierowaną l przechodzącą przez ten punkt.

Niech M(x,y,z) oznacza dowolny punkt tej osi. MoM to odległość między tymi punktami wzięta z odpowiednim znakiem, a mianowicie z + jeśli zwrot MoM pokrywa się ze zwrotem osi l, ze znakiem - w przeciwnym przypadku.

Niech M→Mo. Jeśli istnieje granica lim(M→Mo)

f(M)-f(Mo) / MoM to ona nazywa się pochodna kierunkową funkcji f(M) w kierunku l i oznacza się f(Mo)/ l

Pochodna ta charakteryzuje prędkość zmiany funkcji w punkcie Mo w kierunku l. W szczególności zwykłe pochodne cząstkowe też można rozpatrywać jako pochodne kierunkowe.

Niech teraz f(x,y,z) ma w rozpatrywanym obszarze ciągłe pochodne cząstkowe. Niech oś l tworzy z osiami współrzędnych kąty ,,γ. Wtedy można udowodnić że przy tych założeniach pochodna w kierunku l istnieje i wyraża się wzorami:

f/l= f/x*cos+f/y*cos+f/z*cosγ

5. Pochodne i różniczki wyższych rzędów

• a).Pochodne

Jeśli u=f(x,y,z) ma w pewnym obszarze otwartym D pochodną cząstkowa względem jednej ze zmiennych to pochodna ta będąc sama funkcją zmiennych x,y,z może mieć z kolei w pewnym punkcie pochodne cząstkowe względem tej samej lub dowolnej innej zmiennej. Dla funkcji wyjściowej te ostatnie pochodne będą pochodnymi cząstkowymi drugiego rzędu llub drugimi pochodnymi. Jeśli pierwsza pochodna była obliczona np. wzg. X to jej pochodną względem x,y,z będziemy oznaczali: ²u/x²=²f(x0,y0,z0)/ x²=u'x²

b) Różniczki

Niech w obszarze D będzie określona pewna funkcja n zmiennych f(x1,x2...xn)

Mająca ciągłe pochodne cząstkowe rzędu pierwszego. Wówczas jak wiemy różniczką zupełną du nazywamy wyrażenie: df= f/x1+f/x2+f/xn

Gdzie dx1,dx2,...dxn są dowolnymi przyrostami zmiennych niezależnych x1,x2,...xn. Du jest również pewną funkcją zmiennych x1,x2,...xn. Jeśli założyć istnienie ciągłych pochodnych cząstkowych rzędu drugiego funkcji f to du będzie miało ciągłe pochodne cząstkowe rzędu pierwszego i możemy mówić o różniczce zupełnej d(du), którą nazywamy różniczką rzędu drugiego.

Analogicznie definiuje się różniczki wyższych rzędów.

Zapisujemy: d^ku=(/x1*dx1+/x2*dx2+...+/xn*dxn)^k*u

7. Ekstrema funkcji wielu zmiennych

Niech funkcja u=f(x1,x2...xn) będzie określona w obszarze D i niech punkt (x₁⁰,x₂⁰...x_n⁰) będzie punktem wewnętrznym tego obszaru. Jeśli spełniona jest nierówność f(x1,x2...xn)  (≥) f(x₁⁰,x₂⁰...x_n⁰) to mówimy że w punkcie (x₁⁰,x₂⁰...x_n⁰) jest maksimum (minimum) właściwe. W przeciwnym przypadku max(min) mówimy, że jest niewłaściwe.

Załóżmy że funkcja f(x1,x2...xn) ma ekstremum w punkcie (x₁⁰,x₂⁰...x_n⁰). Wykażemy że jeśli w tym punkcie istnieją skończone pochodne cząstkowe =0

To muszą one wszystkie być równe 0.Warunek konieczny można zapisać:

Df(x₁⁰,x₂⁰...x_n⁰) =0.

• Warunki dostateczne istnienia ekstremum

Podobnie jak u funkcji jednej zmiennej w punkcie stacjonarnym wcale nie musi być ekstremum. Rozpatrzmy przypadek funkcji u=f(x,y).Załóżmy że funkcja ta jest określona i ciągła i ma ciągłe pochodne cząstkowe 1 i 2 rzędu w otoczeniu pewnego stacjonarnego punktu (x0,y0); f'x(x0,y0)=0;f'y(x0,y0)=0

Dla ustalenia czy funkcja ma rzeczywiście w tym punkcie ekstremum czy nie, bada się różnicę tej funkcji. f=f(x,y)-f(x0,y0). Dla uproszczenia oznaczymy druga pochodna wzgl. X w p. (x0,y0) przez a11. f”_x²(x0,y0)=a11,pochodną mieszaną f”xy(x0,y0)=a12; druga wzgl. Y f”y²(x0,y0)=a22.

1.Jeśli ta liczba a11*a22-a12²>0 to funkcja ma w punkcie (x0,y0)ekstremum przy czym jeśli a11>0 minimum, a jeśli a11<0 maksimum.

2. Jeśli ta liczba jest ujemna to ekstremum brak

3. Jeśli ta liczba =0 -najgorszy przypadek- trzeba wyłączyć rachunek różniczkowy

8. Funkcje uwikłane, pochodne, twierdzenia (2)

Załóżmy że wartości dwóch zmiennych x,y związane są ze sobą równaniem, które wtedy gdy wszystkie wyrazy przeniesione są na lewą stronę ma postać F(x,y)=0 1.

Jeżeli dla każdej wartości x z pewnego przedziału istnieje 1 lub kilka wartości y która razem z x spełnia równanie 1. to określona jest tym samym funkcja y=f(x)

Jednoznaczna lub wieloznaczna dla której równość F(x,f(x))=0jest już tożsamością Wzgl. X.

TW1. (istnienia funkcji uwikłanej) Załóżmy że F(x,y) jest określona i ciągła w pewnym prostokącie D; w punkcie (x0,y0) funkcja F(x0,y0)=0; przy stałym x funkcja monotonicznie rośnie(maleje) wraz z y; Wówczas w pewnym otoczeniu punktu (x0,y0) równania 1. określa y jako jednoznaczną funkcję f(x) zmiennej x;

Dla x=x0 ta funkcja przybiera wartość y0=f(x0); Funkcja f(x) jest ciągła.

TW2. (o różniczkowalności funkcji uwikłanej)

Niech: a) Funkcja F(x,y) jest określona i ciągła w prostokącie D. B) w punkcie (x0,y0) funkcja =0. c) pochodne cząstkowe funkcji F9x,y) istnieją i są ciągłe w obszarze D. d) pochodna F'y(x0,y0)0. Wówczas prawdziwe są wnioski z tw1. i funkcja y=f(x) ma ciągłą pochodną.

9.Pojęcie szeregu nieskończonego i jego sumy, własności szeregów, przykłady.

Niech będzie dany pewien nieskończony ciąg liczb a1,a2,...,an (1)

Utworzony z tych liczb symbol a1,a2,...,an=
(2) nazywa się szeregiem nieskończonym a same liczby (1) wyrazami tego szeregu. Dodając kolejno wyrazy szeregu tworzymy nieskończenie wiele sum. a1=S1, a1+a2=S2, a1+...an=Sn (3)

Sumy te nazywają się sumami częściowymi i z szeregiem (2) będziemy zawsze wiązali taki ciąg sum częściowych {Sn}. Lim(n→)Sn=S

Def. Skończoną lub nieskończoną granicę S ciągu sum częściowych Sn gdy n→ nazywamy sumą szeregu a1+a2+...+an=S. Nadając tym samym sens symbolowi (2). Jeśli szereg ma sumę skończoną to nazywamy go zbieżnym inaczej jest rozbieżny.

TW. Na to by szereg był zbieżny potrzeba i wystarcza by dla każdego >0 istniało takie N że dla wszystkich n>Ni dla wszystkich pN zachodziła nierówność:

|an+1 + an+2 + ...an+p|< 

Własności: 1. Jeżeli szereg (2) jest zbieżny to suma rn jego reszty dąży do 0ze wzrostem n lim(n→0)rn =0 2. Odrzucenie skończonej liczby początkowych wyrazów szeregu lub dołączenie na początku skończonej liczby nowych wyrazów nie odbije się na zbieżności szeregu. 3. Jeśli wszystkie wyrazy szeregu zbieżnego (2) pomnożymy przez czynnik stały c to zbieżność szeregu zostanie zachowana a suma ulegnie pomnożeniu przez c. 4. Dwa szeregi zbieżne S1,S2 można dodawać (odejmować) wyraz za wyrazem tak że szereg (a1 b1)+(a2b2)+...+(anbn)... jest także zbieżny a jego suma równa się S1 S2. 5. Wyraz ogólny an szeregu zbieżnego zawsze dąży do 0 ze wzrostem n. Lim(n→) an= 0 - warunek konieczny zbieżności szeregów liczbowych. Nie jest on jednak dostateczny dla zbieżności szeregu.

10. Zbieżność szeregów o wyrazach dodatnich , kryterium porównawcze D'Alemberta, Cauchy'ego, Rahbego.

Niech szereg suma an=a19a2+...+an (1) będzie dodatni czyli an>=0. Wówczas suma częściowa Sn+1=Sn+an+1.

TW. Szereg dodatni (1) ma zawsze sumę. Suma ta jest skończona a zatem szereg jest zbieżny, jeśli sumy częściowe szeregu są ograniczone z góry, a nieskończona w przeciwnym wypadku.

Kryterium porównawcze. TW. Niech będą dane dwa szeregi dodatnie: suma an=a1+a2+...an i suma bn=b1+b2+...bn. Jeśli poczynając od pewnego miejsac zachodzi nierówność an<=bn to ze zbieżności szeregu B wynika zbieżność szeregu A, lub na odwrót.

TW. Jeśli lim(n→) An/Bn = K; K <0,> to gdy K<+to ze zbieżności szeregu B wynika zbieżność szeregu A, gdy K>0 to z rozbieżności szeregu A wynika rozbieżność szeregu B.

Kryterium Cauchy'ego: Porównanie szeregu A z szeregiem geometrycznym suma qⁿ. Utwórzmy dla szeregu A ciąg o wyrazach
@n=
. Jeśli dla dostatecznie dużych n spełniona jest nierówność @n<=q, gdzie q jest liczbą stałą <1 to szereg jest zbieżny, jeśli natomiast począwszy od pewnego miejsca ten ciąg jest >=1 to szereg jest rozbieżny.

TW. Załóżmy że ciąg @n ma granicę (skończoną lub nie). Wówczas gdy @<1 szereg jest zbieżny, a dla @>1 rozbieżny. Gdy @=1 kryterium nie pozwala rozpoznać zachowania się szeregu!!!!!!!!!!!!!!!!!!!!!

Kryterium D'Alemberta: Rozpatrzmy ciąg Dn=an+1/an. Jeśli dal dostatecznie dużych n spełniona jest pn<=q, gdzie q jest liczbą stałą <1 to szereg jest zbieżny. Jeśli zaś począwszy od pewnego miejsca Dn>=1 to szereg jest rozbieżny.

Gdy ciąg ma granicę (skończoną lub nie) to jeśli D<1 -zbieżny, D=1 - nie daje odpowiedzi o zbieżności szeregu.

Kryterium Rahbego. Jeśli dal dostatecznie dużych n spełniona jest nierówność Rn=n[(an/an+1)-1]>=r, gdzie r jest liczbą stałą >1 to szereg jest zbieżny. Natomiast jeżeli poczynając od pewnego miejsca Rn<1 to szereg jest rozbieżny.

Gdy ciąg Rn ma granicę =R przy n→to jeśli R>0 to szereg jest zbieżny gdy R<1 - rozbieżny.

11. Pojęcie zbieżności absolutnej i warunkowej szeregu.

TW. Niech będzie dany dany szereg suma an=a1+a2+...+an. Jeżeli jest zbiezny szereg o wyrazach utworzonych z wartości bezwzględnych wyrazów szeregu A

Suma |an|=|a1|+|a2|+...+|an|+... (A*) to dany szereg jest także zbieżny. Dowód z kryterium Cauchy'ego , bo wtedy nierówność |an+1 + an+2 + an+p|<=|an+1| +|an+2|+...+|1n+p| pokazuje że jeśli warunek konieczny i dostateczny zbieżności jest spełniony dla A* to tym bardziej suma po lewej stronie jest <. Wtedy szereg A jest zbieżny.

Def. Jeżeli szereg A jest zbieżny wraz z szeregiem A* utworzonym z wartości bezwzględnych jego wyrazów to mówimy że szereg A jest absolutnie zbieżny. Na mocy udowodnionego twierdzenia dla bezwzględnej zbieżności szeregu A wystarcza sama tylko zbieżność szeregu A*. Jeśli szereg A jest zbieżny a szereg A* nie jest zbieżny to tylko wtedy szereg A nazywa się warunkowo zbieżnym.

12. Kryterium całkowe zbieżności szeregów, kryterium Leibnitza, Abela, Dirichleta.

Kryterium całkowe: Różni się od wszystkich bo jest oparte na idei porównywania szeregu z całką. Niech szereg ma postać: suma an=suma f(n) (*). Gdzie f(n) jest n^n-1w punkcie x=n pewnej funkcji f(x). f(n)=1 / 3ⁿ+5ⁿ, f(x)=1 / 3^x+5^x, x>=1

Załóżmy że t funkcja jest ciągła dodatnia i monotonicznie malejąca.

Kryterium: Przy wyżej zrobionych założeniach szereg (*) jest zbieżny lub rozbieżny w zależności od tego czy funkcja F(x)=całka f(x)dx ma dla x→ granice ukończoną czy nie czy całka od 0 do  f(x) dx jest zbieżna czy nie. Suma 1/n, f(x)=1/x, całka od 1 do  1/xdx = ln|x|
od 1 do  =+.

TW. Leibnitza: Jeżeli nie wszystkie wyrazy szeregu są dodatnie ale począwszy od pewnego miejsca już takie są to odrzucając dostateczną ilość wyrazów początkowych sprowadzamy rzecz do badania zbieżności szeregu dodatniego. Tak więc nowy będzie przypadek gdy wśród wyrazów szeregu jest zarówno nieskończenie dodatnich jak i nieskończenie wiele ujemnych.

Szeregi takie wygodnie jest zapisywać w ten sposób żeby znaki były wyraźnie wskazane. C1-c2+c3-c4+...+(-1)^n-1cn+... Takie szeregi nazywamy naprzemiennymi. Jeśli ponadto zachodzi nierówność cn+1<cn, lim(n→)cn=0

To zachodzi następujące twierdzenie:

Dla szeregów naprzemiennych dla których są spełnione te dwa warunki szereg jest zbieżny. Suma (-1)^n-1 / n =1-1/2+1/3-1/4...+(-1)^n-1 / n+...; cn =1/n →0 szreg jest zbieżny.

Kryterium Abela: Jeżeli szereg suma bn=b1+b2+b3+...+bn+... jest zbiezny a liczby an tworzą ciąg monotoniczny i ograniczony |an|<=K, n=1,2,... to szereg suma an*bn= a1*b1+a2*b2+...+an*bn+... jest zbieżny.

Kryterium Dirichleta: Jeżeli sumy częściowe szeregu suma bn są wspólnie ograniczone (|Bn|<=M, n=1,2...) a liczby an tworzą ciąg monotoniczny dążący do 0, lim(n→)=0 to szereg suma ab*bn jest zbieżny.

13. Własności szeregów zbieżnych, TW Riemana.

Rozpatrzmy ciąg zbieżny suma an=a1+a2+...+an który oznaczymy przez (A). Będziemy teraz łączyli wyrazy tego szeregu w grupy w dowolny sposób nie zmieniając przy tym jednak ich kolejności. a1+a2+...+an1=b1; an+1, an+2...an2=b2; suma bn (A^).

TW. Szereg A^ jest zawsze zbieżny i ma tą samą sumę co szereg wyjściowy. Innymi słowy szereg zbieżny ma własność łączności. Ta analogia z sumami zwykłymi jednak zostanie zakłócona jeżeli spróbujemy zastosować własność łączności w przeciwna stronę. Czyli jeżeli dany jest szereg A który jest zbieżny to opuszczając nawiasy mamy nowy szereg który może się okazać rozbieżny. Oczywiście jeżeli po opuszczeniu nawiasów otrzymamy szereg zbieżny to jego suma będzie taka sama jak suma szeregu A^.

Niech teraz będzie dany szereg a o sumie A. Przestawiając w tym szeregu wyrazy w dowolny sposób otrzymujemy nowy szereg suma ak=a1'+a2'+...an'=A'

Każdy wyraz ak' tego szeregu jest identyczny z pewnym wyrazem ank szeregu A. Czy szereg A' jest zbieżny, a w przypadku zbieżności czy suma jego jest równa sumie szeregu (a)=A. Do tego musimy przeprowadzić ostre rozróżnienie między szeregami zbieżnymi bezwzględnie i warunkowo.

TW. Jeśli szereg A jest zbieżny bezwzględnie to szereg A' otrzymany z niego przez przestawienie wyrazów jest również zbieżny i ma tą samą sumę A co szereg wyjściowy. Szereg absolutnie zbieżny ma własności przemienności. Jeżeli chodzi o szeregi zbieżne warunkowo to można wykazać że nie są one przemienne. W każdym takim szeregu odpowiednia permutacja wyrazów zmienia sumę szeregu a nawet może zepsuć zbieżność.

TW. Riemana: Jeżeli szereg A jest zbieżny warunkowo to dla każdej z góry zadanej liczby B skończonej lub nieskończonej można wyrazy tego szeregu tak poprzestawiać by przekształcony szereg miał sumę równą B.

14. Mnożenie szeregów.

Niech będą dane dwa szeregi zbieżne: suma an=a1+a2+...an+...=A;

suma bn= b1+b2+...bn+...=B. Naśladując reguły mnożenia sum skończonych rozpatrzymy także i tutaj iloczyny parami ai*bkwyrazów tych szeregów. Utworzą one nieskończoną macierz prostokątną. Iloczyny te można na różne sposoby ustawiać w zwykły ciąg. Można np. uporządkować te iloczyny po przekątnych lub po bokach kwadratów. Po przekątnych: a1*b1; a1*b2; a2*b1; a1*b3; a2*b2; a3*b1 ... Po bokach kwadratu: a1*b1; a1*b2; a2*b2; a2*b1; a1*b3; a2*b3 a3*b3; a3*b2; a3*b1; ... Utworzony z takich ciągów szereg nazywa się iloczynem szeregów A i B.

TW. Cauchy'ego (o mnożeniu szeregów) Jeżeli obydwa szeregi A i B są zbieżne absolutnie to ich iloczyn utworzony z iloczynów powyższej macierzy wziętych w dowolnym porządku jest także zbieżny i ma sumę równą iloczynowi A i B.

W praktyce najlepiej łączyć wyrazy leżące na jednej przekątnej.

15. Szeregi funkcyjne, znieżność jednostajna i niejednostajna.

Przypuśćmy teraz że dany jest ciąg którego wyrazami są funkcje: f1(x), f2(x) ... fn(x)...(1). Funkcje są określone w pewnym obszarze X. Niech dla każdej wartości x należącej do obszaru X ciąg ten ma granicę skończoną. Lim (n→)fn(x)=f(x) (2). Ponieważ jest ona całkowicie wyznaczona przez x jest również funkcją x. Będziemy nazywali ją funkcją graniczną szeregu (1). Będzie nas interesowało teraz istnienie granicy dla każdej poszczególnej wartości x i własności funkcyjne funkcji granicznej. Przypuśćmy, że wszystkie wyrazy ciągu (1) są funkcjami ciągłymi zmiennej x w {a,b}. Czy gwarantuje to ciągłość funkcji granicznej. Własność ciągłości wyrazów czasami przechodzi na funkcję graniczną a czasem nie.

Np. fn(x)=xⁿ {0,1}; f(x) = lim (n→) xⁿ= {0 dla x<0,1); 1 dlax=1

Jeśli jako fn(x) = nx / 1+ n²x² to funkcja graniczna

f(x) = lim(n→) nx / 1+ n²x²=0 <0,)

Rozpatrzmy teraz szereg którego wyrazami są funkcje tej samej zmiennej x w pewnym obszarze X. Suma un(x) =u1(x)+u2(x) + ...+ un(x)+... (3)

Przypuśćmy że ten szereg jest zbieżny dla każdego xX. Wtedy jego suma f(x) jest też pewną funkcją zmiennej x. Suma ta będzie określana przez róność graniczną (2), jeżeli przez fn(x) będziemy rozumieli sumę częściową:

fn(x) = u1(x)+u2(x) + ...+ un(x)+.... Na odwrót funkcję graniczną dla dowolnie zadanego ciągu (1) można badać pod postacią sumy szeregu (3) jeśli przyjmiemy za u1(x) =f1(x), u2(x)  f2(x) - f1(x), u3  f3(x) - f2(x) itd. Jak się okazuje własności funkcyjne funkcji granicznej f(x) czyli co na to samo wychodzi sumy szeregu (3) istotnie zależą od samego sposobu zbliżania się fn(x) do f(x).

Zbieżność jednostajna i niejednostajna.

Przypuśćmy że równość (2) zachodzi dla wszystkich xX. Z samej definicji granicy wynika: Jeżeli tylko ustalimy wartość xX(żeby mieć do czynienia z konkretnym ciągiem liczbowym) to dla dowolnego >0 znajdujemy taki numer N że dla wszystkich n>N spełniona jest nierówność: |f(x) - fn(x)|< (5), gdzie przez x rozumiemy właśnie tę ustaloną poprzednio wartość. Biorąc inną wartość xX otrzymujemy inny ciąg liczbowy. Dla tego samego  otrzymany numer N mógłby się okazać nieodpowiedni, musielibyśmy więc zastąpić go większym. Lecz x przybiera nieskończony zbiór wartości. Otrzymamy więc również nieskończony zbiór różnych ciągów liczbowych zbieżnych do granicy. Dla każdego z nich z osobna znajdujemy odpowiednie N. Czy istnieje taki nr. N który dla zadanego z góry  nadawałby się dla wszystkich ciągów jednocześnie? W pewnych przypadkach takie N istnieje, w innych zaś nie.

Przykład 1. Niech fn(x)=x / 1+n²x² , X=<0,1>; lim(n→) x / 1+n²x²=0, f(x)=0

| x / 1+n²x²|< ; 1/2n*| x / 1+n²x²|<=1/2n; 1/2n<; (1-nx)²>=0; 1-2nx+x²n²>=0

1+ x²n²>=2nx; 1>=2nx / 1+ x²n² ; n>1/2; N=E(1/2)

16. Kryterium Weierstrassa, różniczkowanie szeregów, całkowanie szeregów.

Kryterium Weierstrassa: Jeśli dla wyrazów szeregu funkcyjnego (3) zachodzą w obszarze X nierówności |un(x)|<=cn, gdzie cn- wyrazy pewnego szeregu liczbowego , to szereg (3) jest zbieżny w zbiorze X jednostajnie.

Całkowanie: Jeżeli funkcje un(x) są ciągłe w <a,b> i utworzony z nich szereg suma un(x) = f(x) jest zbieżny jednostajnie w tym przedziale to całka sumy f(x) tego szeregu równa się sumie całek wyrazów tego szeregu. Dopuszczalne jest całkowanie szeregu wyraz za wyrazem.

Różniczkowanie: Niech funkcje un(x) będą określone w <a,b> i mają w tym przedziale ciągłe pochodne un'(x). Jeżeli nie tylko szereg un(x) jest zbieżny jednostajnie w tym przedziale lecz także szereg utworzony z pochodnych jest zbieżny jednostajnie w tym przedziale to suma szeregu un(x) ma w przedziela <a,b> pochodną która równa się sumie szeregów utworzonych z pochodnych jej wyrazów. Szereg można różniczkować wyraz za wyrazem.

21. Całki krzywoliniowe I rodzaju.

Niech będzie dana na płaszczyźnie krzywa nie zamknięta ciągła prostowalna k na której rozmieszczone są masy przy czym gęstosć liniowa ρ(M) w punkcie M jest znana. Należy wyznaczyć masę m całej krzywej k.W tym celu wstawmy pomiędzy końce krzywej które oznaczymy AB dowolną skończoną liczbę punktów a=A0+A1+...An =B Obierając jakikolwiek punkt Mi na łuku Ai Ai+1 obliczmy gęstość ρ(Mi) w tym punkcie. Zakładając że gęstośc jest w przybliżeniu stała we wszystkich punktach tego łuku przez σi otrzymujemy dla masy tego układu mi wyrażenia przybliżone mi=ρ(Mi)σi a dla całej masy szukanej

m suma od i=1 do n ρ(Mi)σi. Oznaczmy przez = max {σ}. Wtedy wzór dokładny na masę krzywej będzie m=lim(→0)sumy od i=1 do n ρ(Mi)σi

Def. Jeżeli przy zmierzaniu →0 suma całkowa ma określoną granicę skończoną którą oznaczymy przez J niezależną od sposobu podziału krzywej k i od wyboru punktów Mi na końcach AiAi+1 to granicę tę nazywamy całką krzywoliniową pierwszego rodzaju funkcji f(x,y) po krzywej i oznaczamy symbolem

J=całka po (k) f(x,y)ds. Tak więc m = całka po (k) ρ(x,y)ds.

Gdy k jest dana w postaci x=(t); y=(t) to J= całka od do  f((t),(t) pierwiastek x'²(t) + y'²(t) dt;; Gdy k dana jest y=g(x) to ds.=pierw. 1+g'²(x)

Wówczas J= całka od a do b f(x,g(x)) pierw. 1+g'²(x). Gdy k dana jest r=r()

Ds.= pierw. r²()+r'²() d i J=całka od do  f(r()cos, r()sin)

pierw. r²()+r'²() d.

17. Szeregi potęgowe, tw. Cauchy'ego - Adamara

Szczególnym przykładem zastosowania tych twierdzeń jest szereg potęgowy postaci: suma od n=0 do  an*(x-x0)ⁿ (1). Za pomocą zamiany zmiennej ten szereg można sprowadzić do postaci: suma jw. an*xⁿ (2) Więc niech będzie dany szereg (2) będący jak gdyby nieskończonym wielomianem ustawionym wg. Potęg x, a liczby a0, a1,a2...an to stałe współczynniki.

Lemat: Jeżeli szereg (2) jest zbieżny dla wartości x*0 to jest on zbieżny absolutnie dla każdej wartości x spełniającej nierówność: |x|<|x*|

Dla x =0 szereg (2) jest oczywiście zbieżny. Istnieją jednak szeregi potęgowe które oprócz tej jednej nie są zbieżne dla żadnej innej wartości x. Podobne szeregi nie są wskazane a więc załóżmy że dla szeregu (2) istnieją takie różne od 0 wartości x=x* dla których szereg jest zbieżny. Rozpatrzymy teraz zbiór bezwzględnych wartości {|x*|}. Zbiór ten może się okazać ograniczony z góry albo nie. W tym ostatnim przypadku dla każdej wartości x znajdzie się na pewno takie x* że |x|<|x*|, a zatem na mocy lematu szereg (2) jest dla tej wartości zbieżny absolutnie. Niech teraz zbiór {|x*|} będzie ograniczony i niech R będzie kresem górnym tego zbioru. Jeśli |x|>R to rzecz jasna szereg jest dla tego x rozbieżny. Weźmy teraz dowolne x spełniające nierówność |x|<R. Z definicji kresu górnego istnieje na pewno takie x* że |x|<|x*| <R, a to na mocy lematu pociąga za sobą absolutną zbieżność szeregu w punkcie x. Tak więc w przedziale (-R,R) szereg (2) jest absolutnie zbieżny. Poza nim rozbieżny. Na końcach przedziału nie można stwierdzić nic ogólnego. Tam w zależności od konkretnego przypadku może wystąpić zarówno zbieżność jak i rozbieżność.

Obszar zbieżności każdego szeregu (2) jest pewnym przedziałem (-R,R) z włączeniem lub wyłączeniem końców. Przedział ten może być także nieskończony, wtedy szereg będzie wszędzie zbieżny. Wewnątrz przedziału szereg jest ponadto zbieżny absolutnie.

Rozpatrzmy ciąg ρ1=|a1|, ρ2=pierw. |a2|,... ρn=pierw. n st. z |an|. Oznaczymy górną granicę tego ciągu przez ρ=lim (n→)ρn=lim (n→)pierw. n. stopnia z |an|

TW. Cauchy'ego - Hadamarda: Promień zbieżności R jest równy R=1/ρ

18. Szeregi Taylora, przykłady.

Szeregi potęgowe są pod wieloma względami podobne do wielomianów. Sumami częściowymi szeregów potęgowych są wielomiany co czyni z szeregów potęgowych wygodne narzędzie do rachunków przybliżonych. W związku z tym staje się bardzo ważne zagadnienie możliwości rozwinięcia danej z góry funkcji na szereg wg. Potęg xⁿ lub (x-x0)ⁿ . Tzn. przedstawienie jej w postaci sumy szeregu (1) lub (2).

Załóżmy że funkcja f(x) ma w przedziale <xo, x0+H> pochodne wszystkich rzędów. Wówczas ze wzoru Taylora f(x)= ... Wskaźnik n można przy tym brać dowolnie duży. f(x)=f(x0)+f'(x0)/1!*(x-x0)+...+f⁽ⁿ⁾(x0)/n!*(x-x0)ⁿ+...

Szereg taki niezależnie od tego czy jest zbieżny czy nie nazywa się szeregiem Taylora funkcji f(x). Współczynniki a0=f(x0) ...an = f⁽ⁿ⁾(x0)/n! noszą nazwę współczynników Taylora.

Przykład: e^x{ρ=lim(n→) pierw. N. stopnia z |an|=lim(n→) pierw. N. st.z 1/n!

=0; R=1/ρ= 1/0=.

22. Całki krzywoliniowe II rodzaju, def. Niezależność od drogi całkowania.

Niech będzie dana krzywa nie zamknięta ciągła AB i niech dana będzie wzdłuż tej krzywej funkcja punktu f(M)= f(x,y). Dzieląc krzywą punktami Ai na części wybieramy na łuku AiAi+1 dowolny punkt Mi o wsp. Mi (i, i) i weźmy w nim wartość funkcji f(Mi)= f(i, i). Wartości te pomnóżmy tym razem nie przez długość łuku AiAi+1 ale przez długość rzutu tego łuku na oś OX. x=xi+1 - xi

y = yi+1 - yi; i utwórzmy teraz sumę od n=1 do n f(i, i)xi

Def. Jeżeli przy zmierzaniu liczby = max {AiAi+1}→0 ma skończoną granicę

Lim (→0) sumy od i=1 do n f(i, i)xi = J niezależną od sposobu podziału krzywej i od wybooru punktów Mi to granicę tę nazywamy całką krzywoliniową drugiego rodzaju po dx i oznaczamy symbolem: J = całka po (AB) f(x,y)dx. (3)Mnożąc podobnie wartości funkcji f(Mi) przez y= yi+1 - yi zamiast xi to jest przez rzut łuku AiAi+1 na oś OY i tworząc sumę otrzymujemy w granicy całkę krzywoliniową drugiego rodzaju po dy i zapisujemy.........

Warunki niezależności od drogi całkowania: Niech w obszarze D dane będą dwie funkcje P(x,y) =P; Q(x,y) = Q. Rozpatrzmy całkę krzywoliniową drugiego rodzaju całka po (AB) Pdx + Qdy (1).. AB jest dowolną krzywa łączącą punkty A i B leżącą całkowicie w obszarze D. Jakie są warunki przy których wartość całki (1) nie zależy od przebiegu drogi AB tj. określone jednoznacznie przez początek drogi A i koniec B? Wszystko zależy od wyrażenia różniczkowego Pdx + Qdy (2)

Podobnie było gdy mówiliśmy o funkcji F(x,y) dwóch zmiennych i o różniczce zupełnej tej funkcji dF=F/x dx + F/ydy które równe jest wyrażeniu (2) gdy P=F/x; a Q=F/y; Ale nie każde wyrażenie typu (2) jest różniczką zupełną czyli nie dla każdego takiego wyrażenia istnieje funkcja pierwotna F(x,y). Okazuje się że całka (1) nie zależy od drogi właśni w tych przypadkach gdy jej wyrażenie podcałkowe jest różniczką zupełną. TW. Na to by całka (1) nie zależała od przebiegu drogi całkowania potrzeba i wystarcza aby wyrażenie (2) było w rozpatrywanym obszarze różniczką pewnej funkcji 2 zmiennych. Jakie są kryteria czy wyrażenie jest różniczką zupełną czy nie? Aby otrzymać to kryterium założymy że w D istnieją i są ciągłe obie pochodne cząstkowe P/y i Q/x Zakładać będziemy że są ciągłe. Przy tym założeniu od razu mamy kryterium:

Jeśli wyrażenie (2) jest rózniczką pewnej funkcji F(x,y) przy czym P=F/x; a Q=F/y to różniczkując to wyrażenie: P/y = ²F/xy i Q/x=²F/yx

Założone ciągłości pochodnych daje równość tych wyrażeń więc mamy

P/y= Q/x.

19. Szeregi Fourierera, współczynniki Fouriera.

Funkcją okresową jest np. Asin(t+) (1) gdzie  związana z okresem zależnością =2/T. Z takich funkcji okresowych możemy tworzyć funkcje bardziej złożone. Jeśli dodamy kilka wielkości typu y0=A0, y1=sin(t+) ... yn=Ansin(nt+n) (2)

Które mają częstość 2, 3 ... n, to otrzymamy funkcję okreoswą ale istotnie różną od wielkości typu (2). Czy można funkcję okresową (t) o okresie T przedstawić w postaci sumy skończonej, lub nieskończonej ilości wielkości okresowych typu (2). Tak gdy rozważamy pełny nieskończony układ wielkości (2). Funkcje tej klasy mają rozwinięcie w szereg geometryczny.

(t)=A0+A1 sin(t+1)+...+An sin(nt+n)...

Jeżeli za zmienną niezależną obierzemy x=t=2t/T to otrzymamy funkcję zmiennej x, czyli f(x) =(x/) dla której rozwinięcie (3) ma postać:

f(x)= A0+suma od n=1 do  A1sin(nx+n) (4)

Rozwijając wyrazy tego szeregu wg. Wzoru na sinus sumy dwóch kątów i przyjmując A0=a0, Ansinn=an, Ancosn=bn , n=1,2... otrzymujemy ostateczną postać rozwinięcia trygonometrycznego.

f(x)=a0+suma (ancosnx+bnsinnx) (5)

Aby ustalić możliwość rozwinięcia trygonometrycznego (5) dal danej funkcji o okresie (5) należy wziąć za punkt wyjścia określone współczynniki a0, a1, ... an.

Załóżmy że f(x) jest całkowalna w przedziale <-,> w ses=nsie właściwym lub niewłaściwym. W ostatnim przypadku załóżmy dodatkowo że ta funkcja jest całkowalna bezwzględnie. Załóżmy ponadto że funkcja ma rozwinięcie (5) i scałkujemy tę równość wyraz za wyrazem od <-,>. Otrzymujemy wtedy:

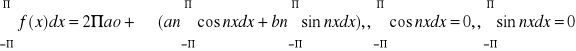
Dlatego wszystkie wyrazy pod znakiem sumy =0 i z tego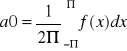

Aby znaleźć an mnożymy obie strony (5) przez cosmx i całkujemy wyraz za wyrazem w <-,>. Wtedy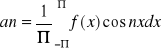
Mnożąc (5) przez sinmx i całkując wyraz za wyrazem mamy: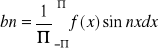
a0, an i bn noszą nazwę współczynników Fouriera, a utworzony przy ich pomocy szereg trygonometryczny nazywa się szeregiem Fouriera.

20. Układy funkcji ortogonalnych, zbieżność szeregu Fouriera, kryterium Libszyca i Dirichleta zbieżności szeregów Fouriera.

Dwie funkcje (x) i (x) określone w przedziale <a,b> nazywamy funkcjami ortogonalnymi w tym przedziale jeżeli całka od a do b (x) * (x)dx =0

Rozważmy układ funkcji {n(x)}, n=1,2,... określony w przedziale <a,b> i całkowalny w nich wraz z kwadratem . Jeśli całka od a do b n(x) *m(x)dx =0

Dal nm to układ nazywamy ortogonalnym układem funkcji w przedziale <a,b>. Zawsze będziemy przy tym zakładali że całka od a do b n²(x)dx =n>0

Czyli że w naszym układzie nie am funkcji tożsamościowo równej 0 ani żadnej funkcji dla której całka z kwadratem byłaby zerem. W szczególności jeśli n=1 dla wszystkich n układ nazywamy układem normalnym. Najważniejszym przykładem ortogonalnego układu funkcji jest właśnie układ (1) 1,sinx, cosx, sin2x, ocs2x...sinnx, cosnx (15) w przedziale <-, > Zauważmy ,żę układ (15) w mniejszym przedziale nie jest już ortogonalny. Natomiast każdy z częściowych układów składających się tyklo z cosinusów lub tylko z sinusów jest już ortogonalny w tym przedziale. Niech w przedziale <a,b> dany będzie dowolny układ ortogonalny {n(x)}. Postawmy sobie za cel rozwinięcie funkcji f(x) okreśonej w przedziale <a,b> na szereg wzzgl. Funkcji n(x) postaci f(x)= c0 n(x)+ c1 n(x)+...cnn(x)+... (20)

Dla określenia współczynników tego rozwinięciaczyli liczb c0,c1,...cn postąpmy tak jak w przypadku szczególnym. Pomnóżmy mianowicie obie strony przez m(x) i scałkujmy je wyraz za wyrazem.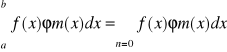

Na mocy ortogonalności układu wszystkie całki po prawej stronie poza jedną =0 i otrzymujemy wzór na cm: cm= 1/m całka od a do b f(x)m(x)dx. Poprzednie wzory na a0, an, bn sa szczególnymi przypadkami tego uogólnionego wzoru. Szereg (20) ze współczynnikami jw. nazywa się uogólnionym szeregiem Fouriera danej funkcji a same współczynniki uogólnionymi współczynnikami Fouriera.

Kyrterium Lipschitza: Szereg Fouriera funkcji f(x) postaci f(x) = a0/2+suma ancosnx+bnsinnx, jest zbieżny w punkcie ciągłości x0 tej funkcji do sumy f(x0) jeśli przy dostatecznie małych wartościach t spełniona jest nierówność:

|f(x0t) - f(x0)|<=L*t^ gdzie  i L są liczbami stałymi, <=1

Ta nierówność charakteryzuje tzw. Warunek Liebschitza. W szczególności warunek Liebschitza przy =1jest f²(x) i ma w p. x0 skończoną pochodną f'(x0)

Tak więc jeśli x0 jest punktem różniczkowalności funkcji to szereg Fouriera jest zbieżny w x0 a jego suma =f(x0). Funkcja f(x0) nazywa się przedziałami monotoniczna w <a,b> jeżeli ten przedział daje się podzielić na skończoną ilość podprzedziałów takich ża wewnątrz każdego z nich funkcja jest monotoniczna.

Kryterium Dirichleta: Jeżeli funkcja f(x) o okresie 2 jest przedziałami monotoniczna w przedziale <-,> i ma co najwyżej skończoną ilość punktów nieciągłości to jej szereg Fouriera ma sumę f'(x0) w każdym punkcie ciągłości i sumę [f(x0-0)+ f(x0+0)]/2 w każdym punkcie nieciągłości.

23.Pojęcie całki podwójnej, def. Własności.

Do pojęcia całki podwójne prowadzi zagadnienie obliczania objętości walca krzywoliniowego. Rozważmy bryłę (V) ograniczoną z góry powierzchnią o równaniu z=f(x,y) (1), z boków powierzchnią walcowa o tworzących równoległych do osi OZ i z dołu figurą płaską (D) na płaszczyźnie XOY. Należy znaleźć objętość bryły (V), w tym celu podzielimy obszar P siatką krzywych na części (P1), (P2), ...(Pn) i rozważymy zbiór małych walców mających dwie części za podstawy i składające się w sumie na bryłę (V). W celu obliczenia objętości poszczególnych walców weźmy w każdej figurze Pi dowolny punkt o wsp. (i, i). Jeżeli w przybliżeniu zastąpimy każdy walec walcem o podstawach równoległych i o wysokości równej rzędnej f(i, i) to objętość walca wyniesie: f(i, i)= Pi; gdzie Pi oznacza pole figury (Pi). Wyrażenie przybliżone na objętość całej bryły ma postać: V suma od 0 do n-1 f(i, i)*Pi. Dla zwiększenia dokładności zmniejszymy wymiary pól Pi. Przechodząc do granicy przy zdążaniu do 0 największej ze średnic obszarów Pi otrzymujemy wyrażenie:

V=lim(→0) suma od i=1 do n f(i, i)*Pi (2) Wzór ten stanowi rozwiązanie zagadnienia. Granice tego typu nazywamy całką podwójną funkcji f(x,y) po obszarze (P) i oznaczamy ... wiesz jak! Sumę od i=1 do n f(i, i)*Pi = σ i nazywamy sumą całkowa dla f(x,y) w (P). Przez oznaczymy największą za średni obszarów częściowych Pi. Skończoną granicę J sumy całkowej σ przy →0

Nazywamy całką podwójną f(x,y) po (P). J= lim(→0)σ= lim(→0)suma od i-1 do n f(i, i)*Pi

Własności. 1). Jeżeli wartość f(x,y) całkowalnej w (P) zmienimy dowolnie wzdłuż jakiejś krzywej L w (P) to otrzymana funkcja będzie również całkowalna w (P) a jaj całka = całka f(x,y) 2). Jeśli (P) w którym dana jest f(x,y) został podzielony krzywa L na dwa obszary (P1), (P2) to z całkowalności funkcji f(x,y) w całym (P) wynika jej całkowalność w obu częściowych (P1) i (P2) i odwrotnie. 3). Jeśli pomnożymy f(x,y) całkowalną w (P) przez stałą k to otrzymana funkcja jest też całkowalna i k przed znak całki. 4). Jeśli w (P) są całkowalne funkcje f(x,y) i g(x,y) to całkowalne są również f(x,y)  g(x,y) przy czym zachodzi rozdzielenie całki sumy na sumę całek. 5). Jeśli całkowalne w (P) f(x,y) i g(x,y) spełniają nierówność f(x,y)<=g(x,y) to całki są tak samo. 6). W przypadku całkowalności funkcji f(x,y) całkowalna jest również |f(x,y)| i zachodzi | z całki |<=całka z ||.

7). Jeśli całkowalna w (P) funkcja f(x,y) spełnia nierówność m<=f(x,y)<=M

t m*P<=całkaf(x,y)dP<=M*P; Jeśli podzielimy tę podwójną nierówność przez P to m<= całka f(x,y)dP / P <=M. Jeśli przez  oznaczymy środkowy iloraz to całka z f(x,y)dP = P; m<=<=M.

24. Obliczanie całki podwójnej.

Rozpoczniemy gdy obszar całkowania jest prostokątem P= <a,b,c,d>

TW. Jeśli dla funkcji f(x,y) określonej w prostokącie P istnieje całka podwójna z f(x,y)dP (1) po (P) przy każdym ustalonym x z przedziału <a,b> istnieje całka pojedyncza J(x) = całka od c do d f(x,y) dy (2) to istnieje także całka iterowana

Całka od a do b J (x)dx =całka od a do b całki od c do d f(x,y)dy dx. I zachodzi równość całka podw. Po (P) f(x,y)dP = całka <a,b>dx całki <c,d> f(x,y)dy (4)

Uwaga! Jeśli wraz z całką podwójną (1) istnieją obie całki pojedyncze całka <c,d>

F(x,y)dy i całka <a,b>f(x,y)dx to słuszny jest wzór (4) i (4) ze zmianą zmiennych (dy,dx) skąd wynika równość tych dwóch całek iterowanych (całka po dx,dy= całka dy,dx).

25. Wzór Greena.

Wyprowadzimy wzór wiążący całkę podwójna z całką krzywoliniową. Rozważmy obszar D trapez krzywoliniowy ograniczony konturem L składającym się z krzywych PQ - y=y0(x); RS - y=Y(x)oraz dwóch odcinków PS i RQ || OY. Załózmy że w obszarze D dana jest funkcja P(x,y) ciągła wraz z pochodną dP/dy. Obliczmy teraz całkę podwójną po obszarze (d) z dP/dy dxdy . Otrzymujemy całkę <a,b> z dx całki <yo(x), Y(x)> dP/dy dy. Całka wewnętrzna =

P(x,Y(x))-P(x,y0(x)) a więc całka podw. z dP/dy dxdy = całka<z,b>[ P(x,Y(x))-P(x,y0(x))]dx = dwie całki... Każda z tych całek może być teraz zastąpiona przez całkę krzywoliniowa. Korzystając ze wzoru na całkę krzywoliniową II rodzaju całka <a,b> f(x,y(x)) dx= całka po (AB) f(x,y) dx. Widzimy ,że 1 całka po (SR) P(x,y)dx - calka po (PQ)P(x,y)dx=suna tylko 2 całka po (QP). Itd. Itp.

Wzór: całka po (L) Pdx + Qdy = całka podw. Po (D) (Q/x - P/y)dxdy

26. Zamiana zmiennych w całce podwójnej.

Załóżmy że dane są dwie płaszczyzny z których jedna jest w układzie x,y; a druga w , . Rozważmy w tych płaszczyznach dwa obszary domknięte. Obszar D na x, y, i  na , . Każdy z nich może być również nieograniczony. O konturze zakładać będziemy że jest to krzywa zwykłą kawałkami gładka. Oznaczmy kontur D δ oraz  dla . Przyjmijmy że w obszarze  dana jest rodzina funkcji ciągłych przy czym różnym punktom (, ) odpowiadają różne punkty (x, y). X= x(, ); y= y(, ) (1). Wtedy równości (1) sa jednoznacznie rozwiązalne względem , 

= (x, y); = (x, y) (1'). W takim razie pomiędzy obszarami D I  usatlona jest odpowiedność wzajemnie jedoznaczna. Mówimy też że wzory (1) określają przekształcenie (1') określają odwzorowanie odwrotne obszaru D na .

Zakładać będziemy że funkcje (1) i (1') są nie tylko ciągłe lecz mają również ciągłe pochodnw cząstkowe. Wyznacznik |x/ x/ dy/ dy/|=J(,)

Ten wyznacznik to jakobian przekształcenia (1) . Gdy x= rcos i y= rsin to jakobian przekształcenia krzywej obiegu na r,  = r.

Całka podw. Po (d) f(x,y)dxdy= całka podw. Po(D)f(x(,), y(,))*|J(,)|dd

27. Pole powierzchni, jednostronność, dwustronność, wybór strony powierzchni.

Ustalmy z początku ważne pojęcie strony powierzchni. Jeżeli powierzchnia dana jest równaniem uwikłanym z=f(x,y) to można mówić o górnej i dolnej powierzchni albo o wewn. I zewn. Stronie. Rozważmy gładką powierzchnię (s) zamkniętą lub ograniczoną konturem kawałkami gładkim. Ponieważ powierzchnia jest gładka więc w każdym punkcie istnieje określona płaszczyzna styczna której położenie zmienia się w sposób ciągły wraz z punktem styczności. Normalna do powierzchni (s) w p. M0 nazywamy prostą przechodzącą przez ten punkt i prostopadłą do płaszczyzny stycznej w p. M0. Biorąc na powierzchni (S) określony punkt M0 prowadzamy w nim normalną której przypisujemy określony kierunek jeden z dwóch możliwych. Poprowadźmy na powierzchni kontur zamknięty wychodzący z p. M0 i powracający do tego punktu., przy czym nie przecina on brzegu obszaru. Niech p. M obiega ten kontur. Może się zdarzyć że albo po obiegu konturu wrócimy do M0 z tym samym kierunkiem normalnej albo z kierunkiem przeciwnym do wyjściowego. W 1 przyp. Powierzchnia nazywa się dwustronną a w 2 jednostronną. Zajmiemy się tylko powierzchniami dwustronnymi. Najprostszym jej przykładem jest powierzchnia opisana równaniem z=f(x,y) przy założeniu że funkcja z jest ciągła w pewnym (D) i ma tam ciągłe pochodne cząstkowe. Wtedy cosinusy kierunkowe normalnej do powierzchni wyrażają się wzorami: normalna a oś Ox: cos= -p /  pierw. 1+p²+q²; wektor normalnej a oś Oy: cos=-q /  pierw. 1+p²+q²; normalna a oś OZ: cosγ=1 /  pierw. 1+p²+q²;Ustalając znak przed pierwiastkiem ustalamy jednocześnie we wszystkich punktach powierzchni określony kierunek normalnej =. Jasne jest więc że wybór znaku przed pierwiastkiem określa stronę powierzchni. Gdy + to cosγ we wszystkich punktach powierzchni będzie>0

Kąt utworzony przez normalną odpowiadającą wybranej stronie i przez OZ będzie ostry. Tak więc strona określona wyborem znaku jest stroną górną. Znaki - w wyrażeniu na cos kierunkowe normalnej charakteryzują dolną str. Powierzchni.

Powierzchnię mającą pole nazywamy mierzalną. Gdy powierzchnia jest podana x= x(u,v); y= y(u,v); z= z(u,v) to S= całka podw. Po () pierw A²+B²+C² dudv

Gdzie A= macierz dy/du, dz/du, dy/dv, dz/dv; B= macierz dz/du, dx/du, dz/dv, dx/dv; C= macierz dx/du, dy/du dx/dv, dy/dz

Zazwyczaj wprowadza się (dx/du)²+(dy/du)²+(dz/du)² = E

)dx/dv)²+(dy/dv)² +(dz/dv)² = G; dx/du*dx/dv+...= F; Wtedy A²+B²+C² = EG-F²

i S=całka podw. Po () pierw. E*G-F²dudv. Gdy powierzchni (s) dana jest równaniem zwykłym uwikłanym z=f(x,y); p=dz/dx; q=dz/dy to S=całka podw. Po () 1+p²+q² )dxdy.

28. Całki powierzchniowe I rodzaju

Całki powierzchniowe I rodzaju stanowią normalne uogólnienie całek podwójnych analogicznie do uogólnienia całek oznaczonych przez całki krzywoliniowe I rodzaju. Niech w punktach pewnej powierzchni (S) dwustronnej kawałkami gładkiej ograniczonej konturem gładkim dana będzie funkcja f(x,y,z). Podzielmy powierzchnię (S) siatką dowolnie poprowadzonych krzywych na części (s1),(s2)...(sn). Biorąc w każdej części (si) dowolny punkt Mi(xi,yi,zi) pomnożymy wartość funkcji w tym punkcie f(Mi) = f(xi,yi,zi) przez pole Si odpowiedniej części (Si) i utwórzmy sumę wszystkich tych iloczynów σ=suma <i=1, n>f(xi,yi,zi), nazwaną sumą całkową. Skończona granica tej sumy całkowej przy dążeniu średnic wszystkich części (Si) do zera nazywa się całką powierzchniową pierwszego rodzaju funkcji f(x,y,z) po powierzchni (S).

J=całka podw. Po (S) f(x,y,z)ds.

29. Całki powierzchniowe drugiego rodzaju.

Pojęcie całki powierzchniowej drugiego rodzaju tworzy się podobnie do pojęcia całki krzywoliniowej drugiego rodzaju. Rozpatrzmy dwustronna powierzchnię (S) kawałkami gładką i ustalmy jedną z jej dwóch stron. Załóżmy że równanie powierzchni jest z=z(x,y,) przy czym punkt (x,y) zmienia się w obszarze (D) na pł. XOY ograniczony konturem kawałkami gładkim. Możliwy jest więc wybór między górna i dolną stroną powierzchni. W 1 przypadku krzywej zamkniętej na powierzchni przypisujemy kierunek obiegu przeciwny do ruchu wskazówek zegara, w drugim zgodny. Dzieląc powierzchnie na części i rzutując każdą taką część odpowiednio zorientowaną na pł. XOY stwierdzamy że kierunek obiegu konturu figury rzutowanej określa także kierunek obiegu konturu rzutu. Kierunek ten pokrywa się z obiegiem przeciwnym do ruchu wskazówek zegara. Jeśli wybrano górną stronę powierzchni (S). Wtedy bierzemy pole rzutu ze znakiem plus , kiedy wybieramy dolną stronę to minus. Niech teraz w punktach danej powierzchni (S) określona będzie pewna funkcja f(x,y,z) = f(M) Podzielmy powierzchnię (S) siatką krzywych na części (S1), (S2)...(Sn) i wybierzmy w każdej części Si punkt Mi(xi,yi,zi) Pomnóżmy teraz wartość funkcji w tym punkcie przez pole Di rzutu części Si na XOY zaopatrzone znakiem w myśl powyższego prawa. Utwórzmy wreszcie sumę całkową σ= suma <i=1,n>f(xi,yi,zi)*Di. Skończoną granicę tej sumy przy dążeniu średnic wszystkich części do 0 nazywamy całką powierzchniową drugiego rodzaju wyrażenia f(x,y,z)dxdy. Po danej stronie powierzchni (S) i oznaczamy symbolem: J= całka podw. po (S) f(x,y,z)dxdy. Wskazówkę którą stronę powierzchni obrano trzeba zawsze dopowiadać.

30. Całka potrójna, własności.

Niech dana będzie pewna bryła (V) o danym rozkładzie gęstości masy σ=σ(x,y,z)

W każdym punkcie M bryły o współrzędnych M(x,y,z). Należy obliczyć masę m tej bryły. Do rozwiązania tego zagadnienia podzielmy bryłę (V) na części (V1), (V2), ... (Vn) i wybierzmy w każdej części po punkcie M(i,i,i). Przyjmijmy w przybliżeniu że w każdej części (Vi) gdzie i=1...n gęstość jest stała i równa się wartości we wziętym punkcie Mi. Wówczas można masę i- tej części zapisać w przybliżeniu w postaci: mi  σ(i,i,i)*Vi; m  suma <i=1,n> σ(i,i,i)*Vi

m=lim(→0) sumy <i=1,n> σ(i,i,i)*Vi. Granice takich sum noszą nazwę całek potrójnych.

Właściwości: 1). Istnienie i wartość całki potrójnej nie zależy od wartości przyjmowanych przez funkcję na skończonej liczbie powierzchni. 2). Jeśli bryła (V) składa się z 2 części (V1), (V2) to całka po (v)= suma całek po (V1) i (V2).

3). Jeśli k jest stała to można ją wypad przed całkę. 4). Gdy w obszarze (V) są dwie całkowalne funkcje g i f to f  g też jest całkowalna. 5). Jeśli całkowalne w (V) f<=g to całki też <=. 6). W przypadku całkowalności f całkowalna jest też funkcja |f| przy czym moduł całki <= całce modułu. 7). Jeśli w całkowalnym obszarze (V) funkcja f spełnia m<=f<=M to m*V<=całka f<=M*V.

31. Zamiana zmiennych w całce potrójnej.

Współrzędne walcowe są połączeniem współrzędnych biegunowych w płaszczyźnie x, y ze zwykłą współrzędną z. Wzory na przejście od wsp. Walcowych do kartezjańskich maja postać: x=rcos, y=rsin; z=z; jakobian= r

Sferyczne x=rsincos; y=rsinsin; z=rcos; jakobian J= r²sin

32. Pojęcie równania różniczkowego, typy.

Rozwiązywanie równania różniczkowego jest w pewnych przypadkach zadaniem odwrotnym do różniczkowania. Równanie jest najprostszym równaniem różniczkowym dy=f(x)dx. Powyższe równanie ma nieskończenie wiele rozwiązań.

Def. Przez najprostsze równanie różniczkowe rzędu I rozumiemy zależność między funkcją niewiadomą zmienną niezależną i pierwszą pochodną funkcji niewiadomej. Rozwiązaniem równania F(x, y, dy/dx)=0 nazywamy każdą funkcje y= (x) która po podstawieniu do równania zamienia je w tożsamość.

Równanie drugiego rzędu ma postać: F(x, y, y', y”) = 0; rzędu n :F(x, y, y', y”, ...yⁿ)= 0

Typy: Równania jednorodne: Równania rzędu 1 dy/dx=f(x,y) nazywamy równaniem jednorodnym, gdy funkcja f jest funkcją jednorodną stopnia zerowego tzn. zachodzi tożsamość f(tx, ty)=f(x, y). Przyjmując t= 1/x mamy f(x, y) =

f(1, y/x)=(y/x).

Równania liniowe. Równaniem liniowym rzędu 1 nazywamy równanie liniowe względem funkcji niewiadomej i jej pochodnej. Ma ono postać: A(x) * dy/dx +B(x)*y+C(x) =0, gdzie A, B, C są danymi funkcjami ciągłymi zmiennej x. Zakładając że A(x)0 możemy obie strony podzielić przez niego.

Dy/dx +P(x)y=Q(x), Jeżeli w szczególności Q(x)=0 to mamy dy/dx + P(x)=0

To nazywamy to równaniem liniowym. Równanie liniowe jednorodne całkuje się przez rozdzielenie zmiennych. Równanie liniowe nie posiada dodatkowych rozwiązań.

---