Ćwiczenie 9 8 marzec 2004
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego
Technologia Chemiczna
Semestr 2
Grupa 4
Sekcja IX
Piotr Jarosz
Wiadomości wstępne.
Jeśli upuścimy jakiś przedmiot, spadnie on na ziemię. Jest to spowodowane siłą ciężkości, czyli grawitacją. Jest to siła powodująca przyciąganie się ciał. Nie tylko Ziemia jest źródłem grawitacji - ma ją także Księżyc. Grawitacja Słońca przyciąga Ziemię oraz pozostałe planety i utrzymuje je na orbitach. Siła oddziaływania grawitacyjnego dwóch ciał zależy od odległości między nimi. Im większa jest odległość, tym mniejsza siła przyciąga je do siebie. Oddziaływanie zależy też od mas obu ciał - większym masom odpowiada większa siła ciężkości.
Kulka zawieszona na nieważkiej i nierozciągliwej nici nazywana jest wahadłem prostym. By wyznaczyć wartość przyspieszenia ziemskiego należy wyznaczyć długość nici, trwanie 100 wahnięć oraz obliczyć okres wahań. Pomiary powtarzamy trzykrotnie dla uzyskania większej dokładności pomiarowej. Wartość przyspieszenia ziemskiego oblicza się ze wzoru na okres wahadła matematycznego: 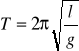
Wychylenia wahadła maleje z czasem wskutek tarcia i oporów powietrza.
Jest to ruch tłumiony. Wykorzystując to zjawisko, można obliczyć tzw. logarytmiczny dekrement tłumienia, czyli wielkość charakteryzująca drgania tłumione. Logarytmiczny dekrement tłumienia to logarytm naturalny stosunku dwóch amplitud w chwilach t i t + T. Chcąc wyznaczyć tą wielkość należy odchylić wahadło od pionu i odczytywać amplitudy kolejnych wahnięć.
Na punkt materialny działa siła ciężkości mg=G skierowana pionowo w dół. Po wychyleniu z położenia równowagi siłę tę rozkładamy na dwie składowe: N- skierowaną wzdłuż nici i P prostopadłą do nici. Siła N napina nić, natomiast składowa P powoduje ruch punktu materialnego ku położeniu równowagi.
![]()
dla małych kątów
![]()
czyli
. ![]()
Dla niewielkich wychyleń wahadło matematyczne porusza się ruchem harmonicznym, w którym przyspieszenie a określone jest równaniem:
, ![]()
gdzie T jest okresem wahań, P = ma , G = mg. Wynika stąd, że
![]()
czyli ![]()
Pomiary
Zmieniając długość wahadła kolejno o 10 cm w dostępnym zakresie (od najmniejszej długości 30 cm do największej 1 m) mierzyć okres drgań wahadła odchylając je o około 5° od położenia równowagi. Należy mierzyć czas co 20 pełnych wahnięć (cykli)
Opracowanie wyników pomiarów
Wykreślić zależność okresu drgań wahadła od pierwiastka kwadratowego jego długości. Metodą regresji liniowej dopasować prostą do zaznaczonych punktów pomiarowych. Z wartości współczynnika kierunkowego (a) dopasowanej prostej wyliczyć wartość przyspieszenia ziemskiego (g):
.
Obliczyć niepewność tej wartości (Δg):
.
Tabela pomiarowa
Liczba okresów: 20
Lp. |
Długość l [cm] |
Czas t [s] |
1 |
30 |
22 |
2 |
40 |
25,43 |
3 |
50 |
27,35 |
4 |
60 |
31,19 |
5 |
70 |
33,53 |
6 |
80 |
35,84 |
7 |
90 |
37,97 |
8 |
100 |
39,90 |
Obliczenia:
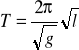
y=ax+b
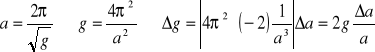
Okres |
|
1,1 |
0,5477 |
1,2715 |
0,63245 |
1,3675 |
0,70710 |
1,5595 |
0,77459 |
1,6765 |
0,83666 |
1,792 |
0,8944 |
1,8985 |
0,9486 |
1,995 |
1,0 |
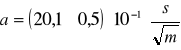
![]()
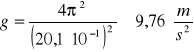
![]()
![]()
Okres [s] |
Długość wahadła [m] |
|
Okres [s] |
Długość wahadła [m] |
1,1 |
0,3 |
|
1,6765 |
0,7 |
1,2715 |
0,4 |
|
1,792 |
0,8 |
1,3675 |
0,5 |
|
1,8985 |
0,9 |
1,5595 |
0,6 |
|
1,995 |
1 |
Wnioski
W ćwiczeniu należało wyznaczyć wartość przyspieszenia ziemskiego. Wyniki uzyskane w niewielkim stopniu różnią się od przyjmowanej wartości 9.81 ![]()
. Odchylenia te wynikają z błędów przy odczycie wartości. Na uwagę zasługuje również fakt, że wartość przyspieszenia ziemskiego nie jest stała i zależy od miejsca na powierzchni Ziemi.
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
wahadlo matematyczne, budownictwo studia, fizyka, wahadło matematyczne
cw2, budownictwo studia, fizyka, wahadło matematyczne
Zadania dodatkowe z AM (5), Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matemat
Lista3, Budownictwo Studia, Rok 2, Statystyka Matematyczna
Wyklad5AM1 2001, Budownictwo-studia, Matematyka
(3609) notacja logiczna, Budownictwo-studia, Matematyka
Statystyka - podstawowe wzory 2, Budownictwo Studia, Rok 2, Statystyka Matematyczna
(848) logika, Budownictwo-studia, Matematyka
WYKLAD 13 ekstrema warunkowe, Budownictwo-studia, Matematyka
wahadło rewersyjne, budownictwo studia, fizyka, wahadło matematyczne
Zagadnienia na egzamin z matematyki dla kierunku Budownictwo, STUDIA, Budownictwo UZ, Semestr I, Mat
Kl2l1(2), Budownictwo-studia, Matematyka
(5170) pochodna funkcji, Budownictwo-studia, Matematyka
Teoria - Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
Lista1 statystyka, Budownictwo Studia, Rok 2, Statystyka Matematyczna
w2z 2004, Budownictwo-studia, Matematyka
analiza1, Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matematyczna
matma zadania, Budownictwo-studia, Matematyka
więcej podobnych podstron