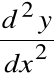WYKŁAD 5
TWIERDZENIE ROLLE'A i LAGRANGE'A, POCHODNE WYŻSZYCH RZĘDÓW
Zastosowanie pochodnych do znajdowania miejsc zerowych funkcji i określania istnienia rozwiązań równań algebraicznych.
Twierdzenie (Rolle'a)
Jeżeli funkcja f jest:
ciągła na przedziale
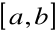
,różniczkowalna na przedziale
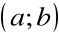
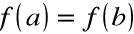
,
to istnieje taki punkt ![]()
, że ![]()
.
Interpretacja geometryczna twierdzenia.
Y f'(c)=0
y=f(x)
a b
0 c X
Uwaga:
Twierdzenie Rolle'a zapewnia istnienie w przedziale ![]()
jednego punktu c, w którym pochodna znika: ![]()
, co nie wyklucza, że punktów takich może być więcej, a nawet nieskończenie wiele, jak to jest na przykład w przypadku funkcji stałej.
Z twierdzenia Rolle'a korzystamy często gdy:
![]()
.
Przykład
Zastosowanie twierdzenia Rolle'a dla funkcji ![]()
w przedziale [0, π],
funkcja ciągła i różniczkowalna
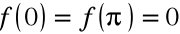
.
Istnieje więc taki punkt ![]()
, że ![]()
. Ponieważ ![]()
, stąd 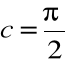
.
Przykład
Zastosowanie twierdzenia Rolle'a do funkcji ![]()
w przedziale [π, 5π]
funkcja ciągła i różniczkowalna
f(π)= -1=f(5π)
![]()
c1=2π, c2=3π, c3=4π
Przykład
Zastosowanie twierdzenia Rolle'a do funkcji
![]()
, w przedziale [-1,1]
funkcja ciągła i różniczkowalna w przedziale (-1,1)
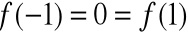
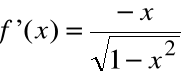
Istnieje c, że ![]()
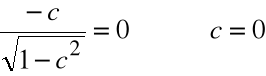
Przykład
Czy można zastosować twierdzenie Rolle'a do funkcji
![]()
w przedziale ![]()
y
f(x)=![]()
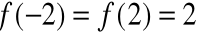
f(x) jest ciągła w przedziale
Nie można zastosować twierdzenia Rolle'a, gdyż funkcja nie jest różniczkowalna we wszystkich punktach przedziału [a,b].
Przykład
Stosując twierdzenie Rolle'a określić ilość rzeczywistych pierwiastków równania
![]()
Wielomian jest stopnia nieparzystego, a zatem istnieje co najmniej jeden pierwiastek rzeczywisty r,
![]()
czy istnieje jeszcze jeden pierwiastek s?
Jeśli tak, to na mocy twierdzenia Rolle'a, istnieje punkt c, miedzy punktami r i s, taki, że
![]()
![]()
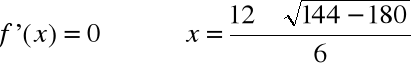
![]()
, a zatem równanie nie ma pierwiastków rzeczywistych
Stąd
![]()
dla każdego x
Wielomian posiada tylko jeden pierwiastek rzeczywisty
Twierdzenie (o przyrostach, Lagrange'a)
Jeżeli funkcja f jest:
ciągła na przedziale domkniętym o końcach
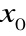
i x,
ma pierwszą pochodną wewnątrz tego przedziału,
to istnieje taki punkt c leżący między ![]()
i x, że
![]()
Niech
![]()
- przyrost funkcji f
![]()
- przyrost zmiennej x
wtedy:
![]()
Stąd nazwa twierdzenie o przyrostach
Interpretacja geometryczna twierdzenia
f(b)
f(x)
f(a)
a x b
Prosta przechodząca przez punkty:
![]()
i ![]()
ma równanie
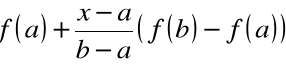
i współczynnik kierunkowy 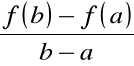
Twierdzenie Lagrange'a mówi, że istnieje punkt ![]()
, że styczna do krzywej w punkcie ![]()
jest równoległa do prostej przechodzącej przez punkty ![]()
i ![]()
Stąd nazwa twierdzenie o przyrostach
Przykład
Zastosowanie twierdzenia Lagrange'a do funkcji
![]()
dla a=1 i b=3.
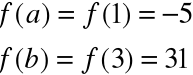
Na mocy twierdzenia istnieje dokładnie jedna wartość c pomiędzy a=1 i b=3, taka, że
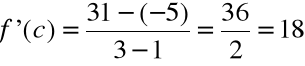
Obliczmy wartość c.
![]()
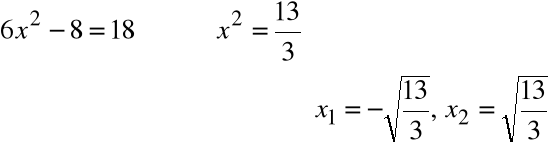

Przykład
(fizyczna interpretacja twierdzenia o przyrostach)
Samochód porusza się wzdłuż osi OX, jego współrzędna w czasie t jest równa f(t).
Np.: w czasie a - współrzędna jest f(a)
w czasie b>a - współrzędna jest f(b)
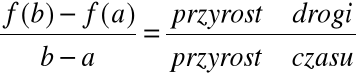
Twierdzenie o przyrostach określa średnią prędkość samochoduWniosek
Jeżeli ![]()
w każdym punkcie przedziału ![]()
,
to funkcja f jest na tym przedziale stała.
Dowód
![]()
, ![]()
![]()
, przy czym ![]()
.
Funkcja f jest różniczkowalna na przedziale ![]()
, a tym samym jest ciągła, więc z twierdzenia o przyrostach:
![]()
![]()
Ponieważ ![]()
, więc ![]()
i ![]()
.
Stąd ![]()
, a zatem ![]()
dla dowolnych dwóch punktów przedziału ![]()
, czyli funkcja f jest na tym przedziale stała.
Jeżeli
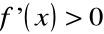
w każdym punkcie przedziału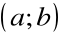
, to funkcja f jest na tym przedziale rosnąca.
Dowód
![]()
, ![]()
![]()
, przy czym ![]()
.
![]()
oraz ![]()
, więc
![]()
, czyli ![]()
.
Jeżeli
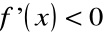
w każdym punkcie przedziału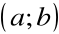
, to funkcja f jest na tym przedziale malejąca.
Uwaga:
Warunek ![]()
(lub ![]()
) dla każdego ![]()
jest wystarczający do tego, aby funkcja f była rosnąca (lub odpowiednio malejąca) na przedziale ![]()
.
Warunek ten nie jest jednak konieczny!
Przykład
Funkcji ![]()
jest rosnąca na każdym przedziale, natomiast ![]()
.
Przykład
Udowodnić, że funkcja
![]()
jest stała.
![]()
a zatem funkcja f(x) jest stała.
Określamy wartość funkcji f(x)
![]()
Stąd ![]()
Wniosek
Jeżeli funkcja f jest rosnąca (lub malejąca) na przedziale ![]()
, w którym jest różniczkowalna, to ![]()
(lub odpowiednio ![]()
) dla każdego ![]()
.
Dowód
Jeżeli funkcja f jest np. rosnąca, to iloraz różnicowy jest dodatni, a więc pochodna (istniejąca z założenia) jest nieujemna.
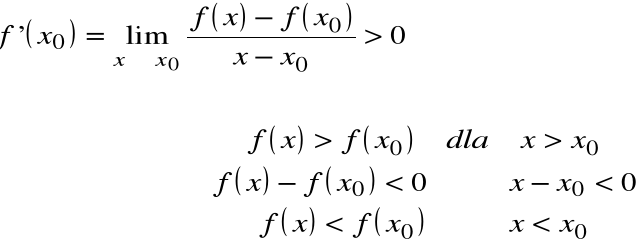
Twierdzenie (Cauchy)
Jeśli:
funkcje f, g:[a, b] Ⴎ [c, d] są ciągłe na przedziale [a, b] ,
pochodne f'(x), g'(x) Ⴙ 0 istnieją dla x (a, b),
to istnieje c (a, b) o własności:
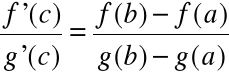
Dowód
Stosujemy tw. Rolle'a do funkcji:
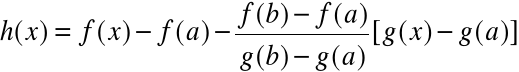
h(a)=h(b)=0,
h - ciągła na [a,b] i różniczkowalna (a,b)
zatem:
dla każdego ![]()
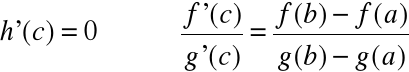
Reguła de l'Hospitala
Chcemy obliczyć:
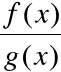
,
gdzie: 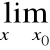
f(x) = 0 = 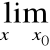
g(x)
lub:
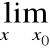
f(x) =![]()
= 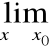
g(x).
Twierdzenie (de l'Hospital)
Załóżmy, że zachodzi jedna z powyższych sytuacji.
Jeśli istnieje 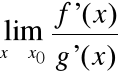
to istnieje: 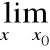
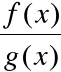
oraz
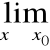
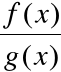
= 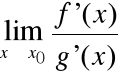
Dowód
Z tw. Cauchy'ego dla f(x0) = 0 = g(x0) i c [x0, x]:
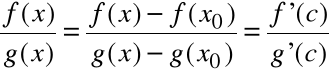
zatem
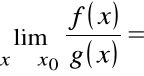
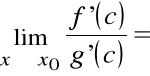
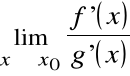
.
Przykład
Obliczyć:
![]()
x e-x
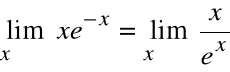
Wyrażenie x / ex jest nieoznaczone dla ![]()
Z reguły de l'Hospitala:
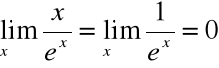
POCHODNE WYŻSZYCH RZĘDÓW
Prędkość - szybkość zmian przebytej drogi
Przyspieszenie - szybkość zmian prędkości
![]()
- miejsce punktu na osi w czasie t
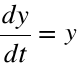
- prędkość poruszania się punktu
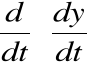
- przyśpieszenie
![]()
![]()
Pochodna pochodnej funkcji f(x) nazywa się
drugą pochodną funkcji f(x)
Oznaczenia:
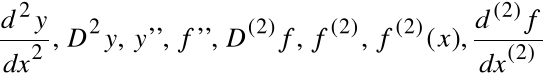
Przykład
![]()
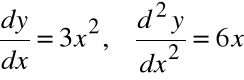
y |
|
|
|
|
6x |
|
|
|
|
|
|
Pochodna drugiej pochodnej funkcji f(x) nazywa się trzecią pochodną funkcji f(x)
Definicja
Definicja indukcyjna pochodnej rzędu n funkcji f, oznaczonej przez f(n):
(i) f(1) = f',
(ii) f(n+1) = (f(n))'.
Będziemy pisali f'' zamiast ![]()
, f''' zamiast ![]()
.
Przykład
f(x)=sinx, f'(x)=cosx, f''(x)=-sinx, f'''(x)=-cosx
Przykład
Obliczyć n-tą pochodna funkcji
![]()
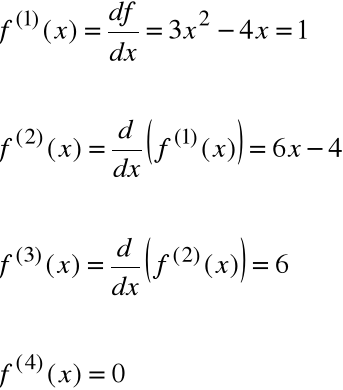
Wszystkie pochodne funkcji f(x) rzędu większego od 3 są równe 0.
Wniosek
Dla każdego wielomianu f(x) stopnia najwyżej 3, ![]()
dla każdego ![]()
.
Przykład
Obliczyć n-tą pochodną funkcji
![]()
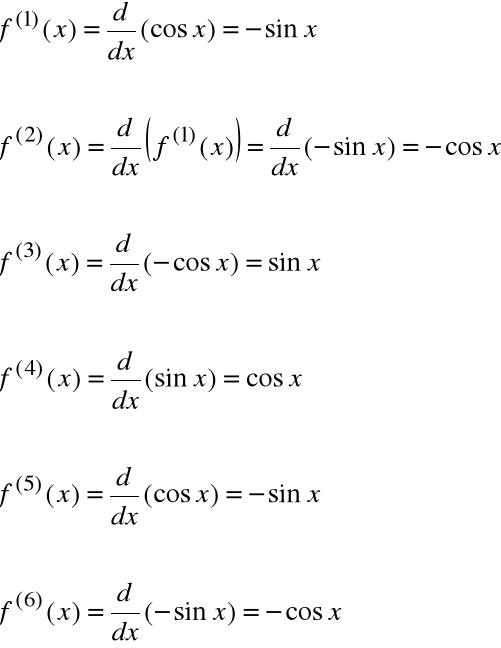
Stąd
![]()
Zastosowanie pochodnych wyższego rzędu:
Druga pochodna funkcji - fizyka
Pochodne wyższych rzędów - określanie błędu aproksymacji np. funkcji przez wielomian
Przykład
Stosując pochodne wyższych rzędów udowodnić, że
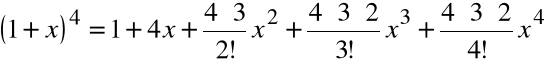
![]()
- wielomian 4-tego rzędu postaci:
![]()
Obliczamy kolejne pochodne obu stron równania:
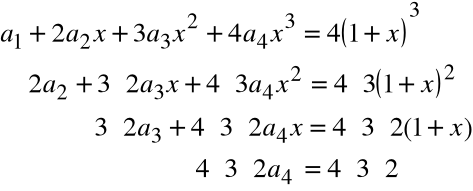
Dla x=0 otrzymujemy odpowiednio z równań
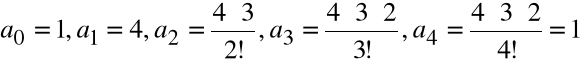
PJWSTK
Analiza Matematyczna 1
Wyszukiwarka
Podobne podstrony:
WYKLAD 13 ekstrema warunkowe, Budownictwo-studia, Matematyka
matematyczne, Budownictwo-studia, Matematyka
(3609) notacja logiczna, Budownictwo-studia, Matematyka
(848) logika, Budownictwo-studia, Matematyka
Kl2l1(2), Budownictwo-studia, Matematyka
(5170) pochodna funkcji, Budownictwo-studia, Matematyka
w2z 2004, Budownictwo-studia, Matematyka
matma zadania, Budownictwo-studia, Matematyka
(3607) zbiory liczbowe, Budownictwo-studia, Matematyka
w1i2-rol-08, Budownictwo-studia, Matematyka
mat, Politechnika Lubelska, Studia, Studia, Sprawozdania, studia, Matematyka, MATEMATYKA WYKŁADY
wykład 6- (05. 04. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
1. Roboty wykończeniowe, budownictwo, STUDIA, sem IId, technologia robót wykończeniowych, wykład
wahadlo matematyczne, budownictwo studia, fizyka, wahadło matematyczne
wykład 9- (17. 05. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
cw2, budownictwo studia, fizyka, wahadło matematyczne
wykład 5- (29. 03. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
Zadania dodatkowe z AM (5), Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matemat
więcej podobnych podstron