Wykład1/2

Podstawowe własności funkcji elementarnych

Kwantyfikatory:

ogólny (duży)
- czyt.: dla każdego x

szczegółowy (mały
- czyt.: istnieje x

Definicja 1. Funkcją określoną na zbiorze D, o wartościach w zbiorze Y, nazywamy takie przyporządkowanie, w którym każdemu elementowi zbioru D przypada dokładnie jeden element zbioru Y.

Elementy zbioru D nazywamy argumentami, zaś elementy zbioru Y wartościami funkcji.

D - dziedzina funkcji

D Y Y - przeciwdziedzina lub zbiór wartości funkcji

D Y

Definicja 2. Niech
. Funkcję f nazywamy różnowartościową (iniektywną lub iniekcją) jeżeli

(lub gdy spełniony jest warunek równoważny:
)

Przykład

Definicja 3. Niech
. Funkcję f nazywamy suriektywną (suriekcją) jeżeli
.

Uwaga: Ta właściwość funkcji zależy istotnie od tego, jak zostanie zdefiniowany zbiór Y. Np.:
nie jest suriekcją, ponieważ

Ale
jest funkcją suriektywną, ponieważ

Przedstawiona na diagramie funkcja jest

Definicja 4. Funkcję
nazywamy bijektywną (bijekcją lub funkcją wzajemnie jednoznaczną) jeżeli jest ona suriektywna i iniektywna.

Definicja 5. Dana jest bijekcja:
.

Funkcją odwrotną do f nazywamy

Uwaga!

Przykłady:

Definicja 6. Niech dane będą funkcje:

Złożeniem (superpozycją) funkcji nazywamy funkcję

Funkcję f nazywamy funkcją wewnętrzną, zaś g - funkcją zewnętrzną.

Przykład:

Wykonaj złożenia w obu porządkach

Wyznacz dziedzinę tych złożeń.

Funkcje elementarne

1. Wielomiany

2. Funkcje wymierne

Dziedzinę funkcji wymiernej stanowi zbiór liczb rzeczywistych z wyłączeniem miejsc zerowych mianownika!!!!

3. Funkcje wykładnicze

przy czym parametr funkcji a>0

4. Funkcje logarytmiczne

przy czym parametr funkcji a>0 oraz

Uwaga: Logarytm istnieje wyłącznie dla liczb dodatnich!!!

5. Funkcje potęgowe

Dziedzina funkcji zależy od wartości parametru p

w szczególności dla
otrzymujemy
i wówczas

Uwaga: Pierwiastek kwadratowy istnieje wyłącznie dla liczb nieujemnych!!!

6. Funkcje trygonometryczne

(Uwaga: Z oznacza zbiór liczb całkowitych)

7. Funkcje cyklometryczne (kołowe) czyli

• Funkcja
  

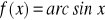
Przyjrzyjmy się własnościom funkcji h(x) = sin x

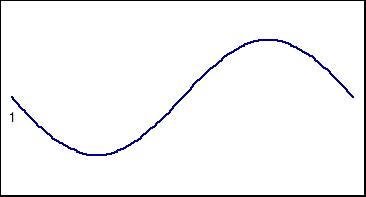
jest funkcją zatem

x	-1				0				1
arc sinx

Pozostałe funkcje cyklometryczne proszę opracować według powyższego wzoru samodzielnie.

• f(x)=arccos x

x	-1				0				1
arc cos x

Opracowanie dr Elżbieta Badach

Na podstawie:

Fichtencholz G.M. Rachunek różniczkowy i całkowy PWN Warszawa 1985

1

a

b

1

2

3

a

b

1

2

3

c

d

a

b

1

2

3

c

4

π

0

---