2. Badanie okresu drgań wahadła o różnej masie i amplitudzie drgań
1. Część teoretyczna
Wahadło proste jest najlepszym odwzorowaniem wahadła matematycznego, którego w praktyce nigdy nie da się zrealizować.
Wahadłem prostym nazywamy mały ciężarek (kulkę) zawieszoną na nierozciągliwej nici. Ciężar nici jest tak mały, że można go pominąć. Zakładamy, że na ruch wahadła nie wpływa opór powietrza. Kulka odchylona o mały kąt od położenia równowagi porusza się ruchem harmonicznym. Można pokazać, że przy tych założeniach, okres ruchu wahadła zależy tylko od długości nici i przyśpieszenia ziemskiego.
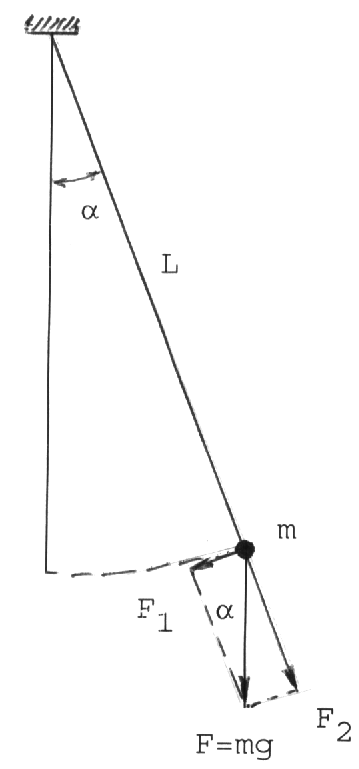
Niech długość wahadła będzie L, a masa kulki - m. Przypuśćmy, że wahadło jest odchylone o mały ( 4o ) kąt α od pionu (patrz rys.). Na kulkę działa pionowo siła przyciągania ziemskiego o wartości F=mg. Składowa F1 siły ciążenia prostopadła do nici jest siłą nadającą ruch wahadłu w kierunku położenia równowagi. Dla małych kątów α:
F1 = -Fsinα = -mgsinα = - mgα
Znak minus oznacza, że siła F1 jest skierowana w kierunku przeciwnym niż ten, w którym odkłada się dodatnie kąty.
Przyspieszenie styczne do toru ciężarka jest równe
α= L![]()
![]()
gdzie ![]()
jest przyspieszeniem kątowym.
Ponieważ składowa F1 jest siłą przyspieszającą masę, to zgodnie z drugą zasadą dynamiki
F1 = ma. Mamy więc:
mL = ![]()
= -mgα , czyli ![]()
= - ![]()
Jest to równanie różniczkowe określające ruch wahadła matematycznego. Ponieważ obie wielkości g i L są dodatnie, to można przyjąć, że ich stosunek równa się kwadratowi pewnej wielkości:
g
- = ω2
L
i równanie różniczkowe przyjmuje postać:
![]()
= -ω2α
Rozwiązaniem tego równania jest wyrażenie określające ruch harmoniczny:
α(t)= Asin(ωt+ϕo)
gdzie A - amplituda kąta,
ϕo - faza początkowa drgania,
ω - częstość kołowa drgania, która wiąże się z okresem T zależnością:
ω = ![]()
.
Stąd mamy
T = ![]()
czyli T = 2π![]()
Z tego wzoru możemy znaleźć wartość przyspieszenia ziemskiego
g jeżeli znamy długość wahadła L i okres T:
g = 4π2![]()
(2)
W przypadku, gdy pomiar długości wahadła jest niemożliwy albo
utrudniony, przyspieszenie ziemskie można obliczyć według wzoru:
g = 4π2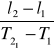
(3)
gdzie l1, l2 poziomy zawieszenia kulki przy różnych długościach wahadła,
T1 , T2 - okresy drgań przy odpowiednich długościach wahadła.
2. Przebieg ćwiczenia
1. Przy ustalonej długości wahadła l zmieniamy masę wahadła oraz amplitudę. Wyniki zapisujemy do tabeli.
2. Aby zwiększyć dokładność pomiarów mierzymy stoperem czas trwania n okresów (n = 10). Pomiary powtarzamy trzykrotnie.
|
Masa / Amplituda |
mała amplituda |
duża amplituda |
mała masa
|
- 19,07 - 19,91 - 19,98 |
- 20,38 - 20,30 - 20,25 |
|
duża masa
|
- 20,28 - 20,10 - 20,25 |
- 20,50 - 20,16 - 20,56 |
|
3. Ocena błędów :
Porównujemy średnie okresy dla małej masy, przy różnych amplitudach :
xi [s] |
(xi - x1) |
(xi - x1)2 |
1,997 |
0,002 |
0,000004 |
1,991 |
-0,004 |
0,000016 |
1,998 |
0,003 |
0,000009 |
5,986 |
|
0,000029 |
xi [s] |
(xi - x2) |
(xi - x2)2 |
2,028 |
0,007 |
0,000049 |
2,010 |
-0,011 |
0,000121 |
2,026 |
0,004 |
0,000016 |
6,063 |
|
0,000186 |
X1 = 5,986 / 3 = 1,995 s
N1 = 3
S1 = √0,000029/3 = 0,003 s
X2 = 6,063 / 3 = 2,021 s
N2 = 3
S2 = √0,000186/3 = 0,008 s
Hipoteza zerowa :
X1 = X2
1,995 s = 2,021 s
Hipoteza alternatywna :
X1 ≠ X2
1,995 s ≠ 2,021 s
£ = 0,05
1 - £ = 0,95
K = N1 + N2 - 2
K = 3 + 3 - 2
K = 4
t£/2 = ± 2,78
Wniosek : Jesteśmy w obszarze krytycznym,
więc hipotezę zerową należy odrzucić.
Wyszukiwarka
Podobne podstrony:
Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
wahadlo matematyczne, budownictwo studia, fizyka, wahadło matematyczne
wahadło rewersyjne, budownictwo studia, fizyka, wahadło matematyczne
Teoria - Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
Wahadło matematyczne, budownictwo studia, fizyka, wahadło matematyczne
Wahadło torsyjne, Budownictwo-studia, fizyka
Badanie drgań tłumionych wahadła sprężynowego, Budownictwo-studia, fizyka
wahadło rewersyjne i wahadło torsyjne, Budownictwo-studia, fizyka
Sprawozdanie 75, budownictwo studia, fizyka
WYZNACZENIE PRĘDKOŚCI DŹWIĘKU METODĄ SKŁADANIA DRGAŃ ELEKTRYCZNYCH 3, budownictwo studia, fizyka
modułu sztywności metodą dynamiczną, Budownictwo-studia, fizyka
ruch drgający, Budownictwo-studia, fizyka
Q, budownictwo studia, fizyka
Sprawozdanie2, budownictwo studia, fizyka
gestosc ciał stałych, Budownictwo-studia, fizyka
Lista3, Budownictwo Studia, Rok 2, Statystyka Matematyczna
wachadło skretne, Budownictwo-studia, fizyka
Wzmacniacz LC - sprawozdanie, budownictwo studia, fizyka
Wyznaczanie ciepla własciwego ciała stał, Budownictwo-studia, fizyka
więcej podobnych podstron