POMIAR KĄTÓW POZIOMYCH METODĄ SCHREIBERA
1. Wprowadzenie
Metoda Schreibera jest stosowana przy pomiarze kątów poziomych w triangulacji głównej. Program obserwacji ułożony jest według następujących założeń:
kąty na danym stanowisku mierzone są we wszystkich kombinacjach,
pomiar każdego kąta wykonywany jest na innym miejscu limbusa,
waga kąta wyrównanego równa się 12, a kierunku wyrównanego 24.
Zakładając, że na stanowisku mamy n kierunków (rys. 1), to ilość wszystkich kątów możliwych do pomierzenia wyniesie: ![]()
Rys. 1 mierzonych kątów na danym stanowisku
przez liczbę kątów niezależnych, otrzymamy ilość przesunięć limbusa, czyli ilość grup kątów niezależnych G. Kąty niezależne i ilość grup kątów niezależnych określone są oddzielnie dla parzystej (rys. 2) i nieparzystej (rys. 3) liczby kierunków n (tabela 1).
Rys. 2, n - parzyste Rys. 3, n - nieparzyste
Tabela 1
|
G |
ilość kątów w grupie |
δ |
n - parzyste |
n - 1 |
|
|
n - nieparzyste |
n |
|
|
Gdyby kąty każdej grupy były mierzone w jednym poczecie, to liczba przestawień limbusa byłaby równa liczbie grup G. Ponieważ każdy kąt mierzony jest w s poczetach, a między poczetami limbus powinien być przestawiony o kąt ![]()
lub ![]()
(gdzie m - ilość mikroskopów),
wszystkich przestawień limbusa będzie:
s (n - 1) - dla n parzystego
sn - dla n nieparzystego
Stąd otrzymujemy, że przy przejściu od pomiaru kątów jednej grupy do drugiej, limbus powinien być przestawiony o kąt δ (tabela 1).
Ilość poczetów oblicza się w założeniu, że waga kąta wyrównanego rówa się 12. Mierzymy ![]()
kątów, z których każdy należy pomierzyć w s poczetach, zatem zrealizujemy ![]()
pomiarów kątowych. Przy n kierunkach chcemy znać wartość (n - 1) kątów. Na jeden kąt wypada więc ![]()
:![]()
pomiarów kątowych. Przyjmując jako wagę kąta liczbę proporcjonalną do liczby pomiarów danego kąta, otrzymamy wzór na wagę kąta: ![]()
, stąd też otrzymamy ilość poczetów: ![]()
.
Ilości poczetów przyjętych dla poszczególnych ilości kierunków mierzonych na stanowisku przedstawia tabela 2.
Tabela 2
n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
s |
12 |
8 |
6 |
5 |
4 |
4 |
3 |
3 |
p |
12 |
12 |
12 |
12,5 |
12 |
14 |
12 |
13,5 |
W celu wyeliminowania błędów systematycznych mikrometru i runu należy także przy obserwacjach kąta w poczetach stosować przesunięcie mikrometru obliczone według wzoru: ![]()
,
gdzie:
w - wartość mikrometru, s - ilość poczetów.
Przy pomiarze kątów metodą Schreibera w triangulacji głównej teodolitem typu Wild T3 wymagane są następujące kryteria:
5. Odchylenie wartości kątów obliczonych z poszczególnych poczetów od wartości kątów wyrównanych na stanowisku |
≤ 3cc ≤ 12cc ≤ 12cc
≤ 5 cc ≤ 6 cc ≤ 7 cc
≤ 9 cc |
2. Ułożenie programu obserwacji
Plan obserwacji dla instrumentu Wild T3 z podziałem stopniowym i gradowym należy ułożyć na podstawie poniższych tabeli, które przedstawiają wartości określające nastawienie limbusa dla pierwszego kierunku. W celu nastawienia limbusa przy pomiarze kąta 2,3, należy do odpowiedniej wartości podanej w tabeli dodać kąt 1,2 (określony z dokłanością 10c lub 10'), przy pomiarze kąta 3,4 dodać kąt 1,3, itp.
4 kierunki (n = 4)
σ = 30o, δ =10o, μ = 20”
Kąt |
Poczety |
|
Kierunek |
2 |
3 |
4 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
I |
II |
III |
1,2 |
0o |
30o |
60o |
90o |
120o |
150o |
|
2 |
|
III |
II |
1,3 |
10 |
40 |
70 |
100 |
130 |
160 |
|
3 |
|
|
I |
1,4 |
20 |
50 |
80 |
110 |
140 |
170 |
|
|
|
|
|
2,3 |
20 |
50 |
80 |
110 |
140 |
170 |
|
|
|
|
|
2,4 |
10 |
40 |
70 |
100 |
130 |
160 |
|
|
|
|
|
3,4 |
0 |
30 |
60 |
90 |
120 |
150 |
|
|
|
|
|
Nast. mikr. |
10” |
30” |
50” |
70” |
90” |
110” |
|
|
|
|
|
σ = 33.3g, δ =11.1g, μ = 1.7c
Kąt |
Poczety |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
1,2 |
0.0g |
33.3g |
66.7g |
100.0g |
133.3g |
166.7g |
1,3 |
11.1 |
44.4 |
77.8 |
111.1 |
144.4 |
177.8 |
1,4 |
22.2 |
55.6 |
88.9 |
122.2 |
155.6 |
188.9 |
2,3 |
22.2 |
55.6 |
88.9 |
122.2 |
155.6 |
188.9 |
2,4 |
11.1 |
44.4 |
77.8 |
111.1 |
144.4 |
177.8 |
3,4 |
0.0 |
33.3 |
66.7 |
100.0 |
133.3 |
166.7 |
Nast. mikr. |
0.8c |
2.5c |
4.2c |
5.9c |
7.6c |
9.3c |
5 kierunków (n = 5)
σ = 36o, δ =7o12', μ = 24”
Kąt |
Poczety |
|
Kier. |
2 |
3 |
4 |
5 |
||||
|
1 |
2 |
3 |
4 |
5 |
|
1 |
I |
II |
III |
IV |
1,2 |
0o00' |
36o00' |
72o00' |
108o00' |
144o00' |
|
2 |
|
III |
IV |
V |
1,3 |
7 12 |
43 12 |
79 12 |
115 12 |
151 12 |
|
3 |
|
|
V |
I |
1,4 |
14 24 |
50 24 |
86 24 |
122 24 |
158 24 |
|
4 |
|
|
|
II |
1,5 |
21 36 |
57 36 |
95 36 |
129 36 |
165 36 |
|
|
|
|
|
|
2,3 |
14 24 |
50 24 |
86 24 |
122 24 |
128 24 |
|
|
|
|
|
|
2,4 |
21 36 |
57 36 |
93 36 |
129 36 |
165 36 |
|
|
|
|
|
|
2,5 |
28 48 |
64 48 |
100 48 |
136 48 |
172 48 |
|
|
|
|
|
|
3,4 |
28 48 |
64 48 |
100 48 |
136 48 |
172 48 |
|
|
|
|
|
|
3,5 |
0 00 |
36 00 |
72 00 |
108 00 |
144 00 |
|
|
|
|
|
|
4,5 |
7 12 |
43 12 |
79 12 |
115 12 |
151 12 |
|
|
|
|
|
|
Nast. mikr. |
12” |
36” |
60” |
84” |
108” |
|
|
|
|
|
|
σ = 40g, δ =8g, μ = 2c
Kąt |
Poczety |
||||
|
1 |
2 |
3 |
4 |
5 |
1,2 |
0g |
40g |
80g |
120g |
160g |
1,3 |
8 |
48 |
88 |
128 |
168 |
1,4 |
16 |
56 |
96 |
136 |
176 |
1,5 |
24 |
64 |
104 |
144 |
184 |
2,3 |
16 |
56 |
96 |
136 |
176 |
2,4 |
24 |
64 |
104 |
144 |
184 |
2,5 |
32 |
72 |
112 |
152 |
192 |
3,4 |
32 |
72 |
112 |
152 |
192 |
3,5 |
0 |
40 |
80 |
120 |
160 |
4,5 |
8 |
48 |
88 |
128 |
168 |
Nast. mikr. |
1,0c |
3,0c |
5,0c |
7,0c |
9,0c |
3. Wyrównanie stacyjne i obliczenie błędów
Wyrównanie obserwacji wykonanych we wszystkich kombinacjach można przeprowadzić dla kierunków lub kątów metodą zawarunkowaną, lub metodą obserwacji pośrednich. Rozpatrzymy metodę pośrenią, wyrównując zaobserwowane kąty.
Dla stanowiska o 4 kierunkach otrzymamy 3 kąty wyrównane, które oznaczymy:
[1,2] [1,3] [1,4]
oraz 6 kątów obserwowanych jako wartości średnie z 6 poczetów:
(1,2) (1,3) (1,4)
(2,3) (2,4)
(3,4)
Określając poprawki do zaobserwowanych kątów przez:
v1,2 v1,3 v1,4
v2,3 v2,4
v3,4
Otrzymamy 6 następujących równań błędów:
v1,2 = [1,2] - (1,2)
v1,3 = [1,3] - (1,3)
v1,4 = [1,4] - (1,4)
v2,3 = - [1,2] + [1,3] - (2,3)
v2,4 = - [1,2] + [1,4] - (2,4)
v3,4 = - [1,3] + [1,4] - (3,4)
Współczynniki przy niewiadomych [1,2], [1,3] i [1,4] wynoszą +1 lub -1.
Otrzymujemy 3 równania normalne:
I 3 [1,2] -1 [1,3] -1 [1,4] = (1,2) - (2,3) - (2,4)
II -1 [1,2] +3 [1,3] -1 [1,4] = (1,3) + (2,3) - (3,4)
III -1 [1,2] -1 [1,3] +3 [1,4] = (1,4) + (2,4) + (3,4)
z których określimy niewiadome, czyli wartości kątów wyrównanych:
[1,2] = ![]()
[1,3] = ![]()
[1,4] = ![]()
Oznaczając:
[1,2] = [2] - [1]
[1,3] = [3] - [1]
[1,4] = [4] - [1]
otrzymamy wzory na kierunki wyrównane: [1], [2], [3] i [4]:
[1] = ![]()
[2] = ![]()
[3] = ![]()
[4] = ![]()
Z powyzszego wyrównania otrzymujemy niezależnie wyrównane kąty, jak również niezależnie wyrównane kierunki. Czyli wyniki z wyrównania stacyjnego mogą być włączane do wyrównania sieci triangulacyjnej i traktowane jako wielkości obserwowane.
Średni błąd pomiaru kąta pomierzonego w jednym poczecie można obliczyć kilkoma sposobami:
na podstawie różnic w - mw
na podstawie różnic d - md
na podstawie różnic v - mv
na podstawie różnic u - mu
gdzie:
w - różnica między wartością kąta średniego z s poczetów a kątem zaobserwowanym w jednym poczecie: wi,k = (i,k) - (i,k)i;
d - różnica między półpoczetami pomiar kąta „tam” i „z powrotem”;
v - różnica między kątem wyrównanym a kątem średnim z poczetów:
vi,k = [i,k] - (i,k);
u - różnica między kątem wyrównanym a kątem zaobserwowanym w jednym poczecie: ui,k = [i,k] - (i,k)i.
Dwie pierwsze grupy różnic są niezależne od kąta wyrównywanego, dwie następne są odchyłkami od kąta wyrównanego.
Wyprowadzenie wzorów dla obliczenia powyższych błędów opiera się na określeniu liczby spostrzeżeń nadliczbowych.
Określenie błędu mw:
mw = 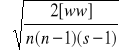
.
Określenie błędu md:
md = 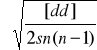
.
Określenie błędu mv:
mv = 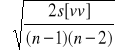
.
Określenie błędu mu:
mu = 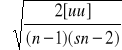
.
Średni błąd kąta wyrównanego mo obliczamy ze wzoru:
mo = 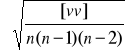
.
W założeniu metody Schreibera wynika, że waga p kąta wyrównanego wynosi 12, czyli p = ![]()
. Znając średni błąd kąta pomierzonego w jednym poczecie mv z wagą p = 1, średni błąd kąta możemy również określić ze wzoru:
mo = ![]()
3
Pomiar kątów poziomych metodą Schreibera
2
1
1
Natomiast kątów koniecznych do zaobserwowania będzie: n - 1.
Ilość nadliczbowych obserwacji otrzymamy z różnicy: ![]()
- (n-1) = ![]()
W celu spełnienia drugiego warunku, obserwacje należy przeprowadzić w taki sposób, aby na tym samym miejscu limbusa były mierzone kąty niezależne. Dzieląc liczbę
4
![]()
2
3
![]()
1
2
3
4
5
6
3
4
5
Wyszukiwarka
Podobne podstrony:
wyklady z kartografii, Geodezja, rok 2, Kartografia
wyklady budownictwo, geodezja, ROK II, Zarys budownictwa
Pytania z wykładu 10 - grupa 5, geodezja, rok III, Podstawy Rolnictwa i Leśnictwa
wykład nr 5, geodezja, rok III, Podstawy Rolnictwa i Leśnictwa
budownictwo wykłady semestr III, Geodezja, rok 2, zarys budownictwa
budownictwo wyklady, geodezja, ROK II, Zarys budownictwa
Zal-lab-BP-zaoczne, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
test-B, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
03 Parzydełkowce, I rok, I semestr, Systematyka zwierząt, wykłady
test-d(1), politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
04 Płazińce, I rok, I semestr, Systematyka zwierząt, wykłady
Ceny usług turystycznych wyk3, Geografia 2 rok, Ekonomiczne podstawy turystyki, Wykłady
ogólne - wykład 10, III ROK, I semestr, Językoznawstwo ogólne - wykład
doskonala prezentacja, geodezja, ROK II, Zarys budownictwa
więcej podobnych podstron