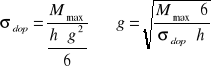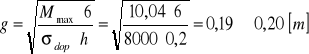OBLICZENIE DŁUGOŚCI DORGI FILTRACJI POD BUDOWLĄ

Schemat obliczeniowy

1.) Metoda Bligh'a:

C_B - współczynnik ustalony przez autora, zależny od rodzaju gruntu (dla żwirów 5Ⴘ9)

- warunek spełniony

2.) Metoda Lena:

C_L - współczynnik ustalony przez autora, zależny od rodzaju gruntu (dla żwiru grubego 3)

- warunek spełniony

OBLICZENIE WNĘK REMONTOWYCH

Schemat obliczeniowy

SPRAWDZENIE GRUBOŚCI NIESKI WYPADOWEJ

k_w -współczynnik na wypłynięcie dla IV klasy budowli =1,05

Ponieważ minimalna grubość płyty może być 0,30 [m] dlatego przyjmuję tą wartość.

ZESAWIENIE CIĘŻARÓW

Ciężar doku	GD=2950,8 [kN]
Ciężar filara	GF=467,3 [kN]
Ciężar zasuw	GZ=32,2 [kN]
Ciężar urządzenia wyciągowego	GW=24,0 [kN]
Ciężar kładki	GK=8,4 [kN]
Ciężar wody górnej	GWG=403,6 [kN]
Ciężar wody dolnej	GWD=1422,6 [kN]

Parcie wody górnej	H1=541,0 [kN]
Parcie wody dolnej	H1=192,9 [kN]
Parcie filtracyjne	PF=849,9 [kN]
Siła wyporu	PW=806,1 [kN]

Sprawdzenie warunku na przesunięcie:

μ - współczynnik tarcia na styku fundamentu z podłożem; =0,55 wg PN 83/B - 03010 tab. 3

dla gruntów niespoistych, żwiry i pospółki, i betonu chropowatego.

G= G_D+ G_F+ G_Z+ G_W+ G_K+ G_WG+ G_WD

G =2950,8+467,3+32,2+24,0+8,4+403,6+1422,6=5308,9 [kN]

U= P_F+ P_W=849,9+806,1=1656,0 [kN]

W_x=H₁-H₂=541,0-192,9=348,1 [kN]

Sprawdzenie warunku na obrót:

Tabela 1. Zestawienie momentów utrzymujących

Lp.	Siła [kN]	Ramie siły [m]	Moment [kNm]
1	GD=2950,8 [kN]	6,62	19534,3
2	GF=467,3 [kN]	10,74	5018,8
3	GZ=32,2 [kN]	11,00	354,2
4	GW=24,0 [kN]	11,00	264,0
5	GK=8,4 [kN]	10,10	84,8
6	GWG=403,6 [kN]	12,20	493,9
7	GWD=1422,6 [kN]	5,42	7710,5
8	H1=192,9 [kN]	0,68	131,2
			33591,7

Tabela 1. Zestawienie momentów obracających

Lp.	Siła [kN]	Ramie siły [m]	Moment [kNm]
1	H1=541,0 [kN]	1,12	6911,3
2	PF=849,9 [kN]	8,64	7343,1
3	PW=806,1 [kN]	6,62	5336,4
			19590,8

233,53

234,90

PN

d_n=0,35

SNW

0,30

H=1,37

0

1

2

3

g

q

W

b_uε

H=2,75

l=3,93

F

W

PN

234,90

h=0,2

Q'

1 m

x

1 m

Q

g

x

g

g