Nr ćwiczenia 206	Data 11.04.2005	Michał Łuszczyński Roman Moch	Wydział MRiT	Semestr IV	Grupa 2
Prowadzący: dr inż. Adam Buczek			Ocena

TEMAT: Pomiar stosunku e/m metodą odchyleń w polu magnetycznym.

Na posiadającą ładunek elektryczny cząstkę, poruszającą się w polu elektrycznym i magnetycznym, działa siła, zwana siłą Lorentza, określona wzorem:

, (1)

gdzie: q - ładunek cząstki, v - jej prędkość, E - natężenie pola elektrycznego, B - indukcja magnetyczna. Działanie obu p*l prowadzi w ogólnym przypadku do zmiany wektora prędkości - w polu elektrycznym może się zmieniać kierunek i wartość prędkości, natomiast w polu magnetycznym wartość prędkości pozostaje stała, a zmienia się kierunek. Badanie zachowania się cząsteczek naładowanych, np. elektronów, protonów w polach elektrycznym i magnetycznym pozwala wyznaczyć tzw. ładunek właściwy, czyli stosunek q/m. W celu określenia naboju właściwego elektronu (e/m) posłużymy się lampą oscyloskopową z odchylaniem magnetycznym w kierunku Y. Pole magnetyczne wytwarzane jest w wyniku przepływu prądu przez uzwojenie umieszczone na zewnątrz lampy. Indukcja magnetyczna B jest proporcjonalna do natężenia prądu I:

. (2)

Współczynnik proporcjonalno*ci c określamy empirycznie. Po wyjściu z obszaru pola magnetycznego elektrony biegną w linii prostej i w końcu uderzają w ekran fluorescencyjny, wywołując jego świecenie. Znajdziemy wyrażenie pozwalające wyznaczyć stosunek e/m z położenia plamki świetlnej na ekranie. Warunek równowagi siły odchylającej w obszarze pola magnetycznego i siły bezwładności wyraża równanie:

, (3)

gdzie R jest promieniem krzywizny toru. Szukaną wielkość e/m można na podstawie tego równania przedstawić w postaci:

. (4)

Prędkość można wyrazić przez napięcie U_a, przyrównując energię kinetyczną do pracy wykonanej przez pole elektryczne na drodze między katodą i anodą:

. (5)

Obliczoną z powyższego równania prędkość wstawiamy do równania (4), podnosimy obie strony do kwadratu i otrzymujemy:

. (6)

Promie* krzywizny R można natomiast wyrazić w postaci:

, (7)

gdzie: l -odległość ekranu lampy oscyloskopowej od środka cewki, d-średnica cewki odchylającej, y- odchylenie plamki na ekranie względem położenia przy B=0. Po wstawieniu wzorów (2) i (7) do równania (6) otrzymujemy wyrażenie, z którego możemy wyliczyć stosunek e/m na podstawie prostych pomiarów.

1. Szukaną wartość e/m wyznaczam ze wzoru:

gdzie:

, w dalszych obliczeniach wielkość tą oznaczymy przez M.

y - średnie odchylenie plamki na ekranie względem położenia zerowego (Odczytane położenie plamki na ekranie przy zerowym prądzie cewki wynosiło 11,5 cm).

I - natężenie prądu wywołujące odchylenie plamki.

2. Ładunek właściwy elektronu dla każdego odchylenia:

Jednostka: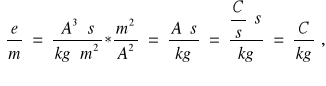

Przykład obliczeń:

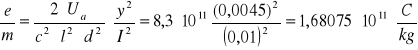
TABELA obliczeń:

	y [m]	I^2 [A^2]	y^2 [m^2]	*10^11
0,0082	0,005	0,000067	0,000025	3,086
0,0198	0,010	0,000392	0,000100	2,117
0,0305	0,015	0,000930	0,000225	2,008
0,0422	0,020	0,001781	0,000400	1,864
0,0525	0,025	0,002756	0,000625	1,882
0,0624	0,030	0,003894	0,000900	1,918
0,073	0,035	0,005329	0,001225	1,908
0,0824	0,040	0,006790	0,001600	1,956
0,0937	0,045	0,008780	0,002025	1,914
0,1041	0,050	0,010837	0,002500	1,915
0,1137	0,055	0,012928	0,003025	1,942
0,1244	0,060	0,015475	0,003600	1,931
0,1326	0,065	0,017583	0,004225	1,994
0,0143	0,005	0,000204	0,000025	1,015
0,0264	0,010	0,000697	0,000100	1,191
0,0371	0,015	0,001376	0,000225	1,357
0,0511	0,020	0,002611	0,000400	1,271
0,0613	0,025	0,003758	0,000625	1,381
0,0711	0,030	0,005055	0,000900	1,478
0,0816	0,035	0,006659	0,001225	1,527
0,0918	0,040	0,008427	0,001600	1,576
0,1018	0,045	0,010363	0,002025	1,622
0,1116	0,050	0,012455	0,002500	1,666
0,1203	0,055	0,014472	0,003025	1,735
0,1304	0,060	0,017004	0,003600	1,757
0,139	0,065	0,019321	0,004225	1,815

• Stąd średnia wartość
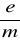
  wynosi: (1,763 ± 0,392)* 10¹¹

3. Wnioski:

Tablicowa wartość naboju właściwego wynosi
.

Dokonany przez nas pomiar naboju jest bardzo zbliżony do tablicowego.

Zatem można uznać, że doświadczenie zostało przeprowadzone prawidłowo.

---