1. Dana jest funkcji f(x) określ zbiór wartości, monotoniczność, miejsce zerowe, punkt przecięcia z osią OY, najmniejszą i największą wartość funkcji, argumenty, dla których funkcja przyjmuje wartości dodatnie oraz argumenty, dla których funkcja przyjmuje wartości ujemne, jeżeli:

a)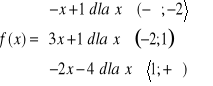
b)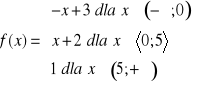

2. Funkcja f(x) określona jest wzorem
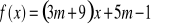
   . W zależności od parametru m określ:

1. monotoniczność funkcji

2. liczbę rozwiązań równania f(x)= -1

3. dla jakiej wartości parametru m punkt przecięcia z osią OY wynosi 4.

3. Znajdź wzór funkcji prostopadłej do f(x) i przechodzącej przez punkt K, jeżeli:

1. 
   
   

2. 
   
   

3. 
   
   

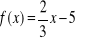
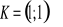
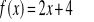
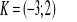
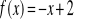
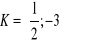
4. Znajdź wzór funkcji równoległej do f(x) i przechodzącej przez punkt K, jeżeli:

1. 
   
   

2. 
   
   

3. 
   
   

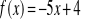
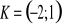
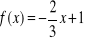
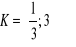
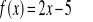
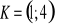
5. Znajdź wzór funkcji f(x) wiedząc, że do wykresu funkcji należą punkty P i M.

1. 
   

2. 
   

3. 
   

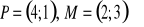
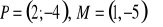
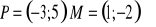
6. Dana jest funkcja
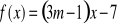
   . Wyznacz parametr m, aby miejscem zerowym funkcji była liczba -3.

7. Zapisz wzór funkcji
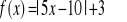
   bez symbolu wartości bezwzględnej. Warunki dla x zapisz w postaci przedziałów.

8. Dana jest funkcja liniowa z parametrem m,
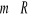
   o wzorze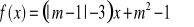
   . Wskaż zdanie prawdziwe:

1. dla m=-1 funkcja jest malejąca i nieparzysta.

2. dla
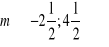
   wykres funkcji jest prostopadły do prostej o równaniu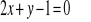
   

3. istnieje taka wartość parametru m, dla której funkcja jest okresowa.

9. Zależność temperatury w skali Fahrenheita od temperatury w stopniach Celsjusza wyraża wzór
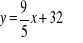
   , gdzie y i x to odpowiednio temperatury w skali Fahrenheita i Celsjusza.

1. Oblicz, w jakiej temperaturze w skali Fahrenheita wrze woda, zakładając, że woda wrze w temperaturze 100
   C.

2. Temperatura wody w basenie wynosi 68
   F. Wyraź tę temperaturę w 
   C.

10. Wyznacz punkt przecięcia wykresów funkcji liniowych
    .

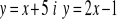
11. Dany jest układ równań liniowych z parametrem m
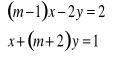
    . Zbadaj liczbę rozwiązań układu ze względu na parametr m.

12. Dana jest prosta l o równaniu
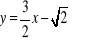
    oraz punkt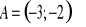
    . Wykres funkcji liniowej f jest prostopadły do prostej l, punkt A należy do wykresu funkcji f. Wyznacz:

1. wzór funkcji f

2. miejsce zerowe funkcji f.

13. Dla jakich wartości parametru m rozwiązaniem układu równań
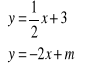
    jest para liczb należąca do II ćwiartki układu współrzędnych?

14. Rozwiąż nierówność
    .

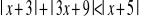
15. Wyznacz funkcję liniową, dla której spełniony jest warunek
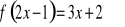
    dla każdej liczby rzeczywistej.

16. Rysunek przedstawia prostą w układzie współrzędnych. Wyznacz równanie tej prostej.

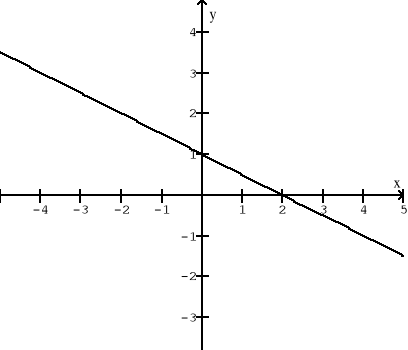
1. Oblicz odległość punktu o współrzędnych (2; 1) od narysowanej prostej.

2. Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i prostopadłej do narysowanej prostej.

17. Funkcja f przechodzi przez punkty
    .

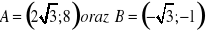
1. Wyznacz wzór funkcji f.

2. Podaj miejsce zerowe funkcji f.

3. Dla jakich argumentów funkcja f przyjmuje wartości większe od -3?

18. Funkcja f określona na zbiorze liczb całkowitych nieujemnych przyporządkowuje każdej liczbie n resztę z dzielenia tej liczby przez 4.

1. Określ zbiór wartości funkcji f.

2. Podaj zbiór wszystkich miejsc zerowych funkcji f.

3. Narysuj wykres funkcji f dla n < 10.

19. Rysunek przedstawia fragment wykresu funkcji liniowej f. Wykres funkcji g jest obrazem wykresu funkcji f otrzymanym za pomocą przesunięcia o wektor
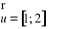
    . Wyznacz miejsce zerowe funkcji g.

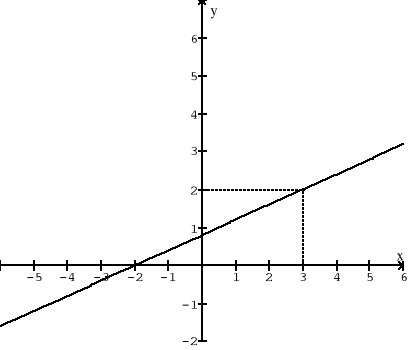
20. Opisz za pomocą układu nierówności zbiór wszystkich punktów należących do trójkąta ABC przedstawionego na rysunku. Oblicz pole tego trójkąta.

21. Z powodu złego stanu torów na trasie z miasta A do miasta B średnia prędkość pociągu zmniejszyła się o 10 km/h. W związku z tym czas podróży na tej trasie zwiększył się z 4 godzin do 4 godzin i 30 minut. Oblicz odległość między tymi miastami.

22. Do figury f należą punkty, których współrzędne spełniają warunki:

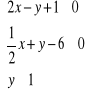
1. Zaznacz w układzie współrzędnych figurę f.

2. Oblicz pole tej figury.

23. Dane jest równanie postaci:
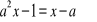
    , w którym niewiadomą jest x. Zbadaj liczbę rozwiązań tego równania, w zależności od parametru a.

24. Narysuj wykres funkcji
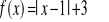
    określonej dla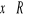
    , a następnie na jego podstawie podaj liczbę rozwiązań równania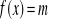
    w zależności od parametru m.

25. Dana jest funkcja
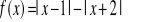
    dla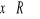
    .

1. Wyznacz zbiór wartości funkcji f dla
   .

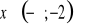
2. Naszkicuj wykres tej funkcji.

3. Podaj miejsca zerowe.

4. Wyznacz wszystkie wartości m, dla których równanie
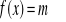
   nie ma rozwiązania.