Na podobnej zasadzie możemy szacować nieznany poziom zjawiska z przeszłości, przy założeniu że średnie tempo zmian w okresie poprzedzającym okres badany było takie samo.
Cd. Przykładu
Mając dane:
![]()
![]()
Możemy obliczyć:
![]()
gdzie „0” - okres bezpośrednio poprzedzający okres numer „1”,
czyli ![]()
to liczba dzieci w szkole w 2000 r.)
![]()
„-1” - okres bezpośrednio poprzedzający okres numer „0”,
czyli ![]()
to liczba dzieci w szkole w 1999 r.
Ogólny wzór na poziom zjawiska w okresie poprzedzającym:
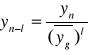
gdzie:
l - liczba okresów (momentów) wstecz od okresu n
l = 1, 2, …
np.: jeśli n=1 oznacza rok pierwszy badany (2001 r.), to:
przyjmując l=1 wyznaczymy poziom zjawiska w roku 2000,
przyjmując l=2 wyznaczymy poziom zjawiska w roku 1999, itd.
Zależności między indeksami jednopodstawowymi a łańcuchowymi
Uwaga !!!
Przekształcenia wykonujemy operując indeksami wyrażonymi w ułamkach
(nie w %)
kolejne dzielenie indeksów jednopodstawowych przez
indeks jednopodstawowy dla okresu k
indeksy jednopodstawowe indeksy jednopodst.
(gdy podstawą jest okres t = 1) (o dowolnej podstawie k)
Np.: gdy podstawą jest okres k = 3
![]()
![]()
![]()
![]()
itd.
Przykład:
(kolumna dana) (kolumna szukana)
t |
yt |
Indeks jednopodstawowy i t /1 |
Indeks jednopodstawowy i t /3 |
1 2 3 4 5 6 |
y1 y2 y3 y4 y5 y6 |
1 0,99 1,02 1,07 1,31 1,19 |
0,98 (bo 1:1,02=0,98) 0,97 (bo 0,99:1,02=0,97) 1 (bo 1,02:1,02=1) 1,05 (bo 1,07:1,02=1,05) 1,28 (bo 1,31:1,02=1,28) 1,17 (bo 1,19:1,02=1,17) |
dzielenie dwóch kolejnych indeksów jednopodstawowych
(„późniejszy” przez „wcześniejszy”)
indeksy jednopodstawowe indeksy łańcuchowe
![]()
![]()
![]()
Np.:
![]()
![]()
![]()
![]()
itd.
Przykład:
(kolumna dana) (kolumna szukana)
t |
yt |
Indeks jednopodstawowy i t /1 |
Indeks łańcuchowy i t /t-1 |
1 2 3 4 5 6 |
y1 y2 y3 y4 y5 y6 |
1 0,99 1,02 1,07 1,31 1,19 |
- (nie da się obliczyć) 0,99 (bo 0,99:1=0,99) 1,03 (bo 1,02:0,99=1,03) 1,05 (bo 1,07:1,02=1,05) 1,22 (bo 1,31:1,07=1,22) 0,91 (bo 1,19:1,31=0,91) |
mnożenie kolejnych (od pierwszego włącznie)
indeksów łańcuchowych
indeksy łańcuchowe indeksy jednopodstawowe
![]()
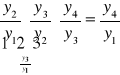
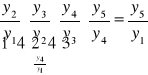
Np.:
![]()
![]()
![]()
itd.
Przykład:
(kolumna szukana) (kolumna dana)
t |
yt |
Indeks jednopodstawowy i t /1 |
Indeks łańcuchowy i t /t-1 |
1 2 3 4 5 6 |
y1 y2 y3 y4 y5 y6 |
1 (bo i 1/1=1) 0,99 (bo i 2/1=0,99) 1,02 (bo 0,99*1,03=1,02) 1,07 (bo 0,99*1,03*1,05=1,07) 1,31 (bo 0,99*1,03*1,05*1,22=1,31) 1,19 (bo 1,31*0,91=1,19) |
- 0,99 1,03 1,05 1,22 0,91 |
Indeksy indywidualne cen, ilości i wartości
różnych produktów (spożywanych, produkowanych),
określają one zmiany cen, ilości i wartości w okresie badanym w stosunku do okresu podstawowego dla każdego produktu odrębnie.
![]()
![]()
![]()
ceny ilości wartości
(w okresie „n” i okresie „0”)
![]()
- tzw. równość indeksowa.
Indeksy agregatowe
- służą do pomiaru dynamiki zjawisk złożonych, tzw. agregatów (zbioru wielu zjawisk jednorodnych)
Np.:
Zjawiskiem złożonym jest:
produkcja przedsiębiorstwa wytwarzającego towary o różnych wartościach użytkowych (np. materiały tekstylne, odzież sportowa)
wielkość sprzedaży hurtowni artykułów spożywczych
produkcja globalna.
Zjawiska złożone (w odróżnieniu od jednorodnych) nie mogą być sumowane i porównywane w naturalnych jednostkach, gdyż jednostki pomiaru są różne (np. sztuki, metry, kilogramy).
prosty
Laspeyresa (stała jest ilość z okresu podstawowego q0)
Indeksy agregatowe cen
Paaschego (stała jest ilość z okresu badanego qn)
Laspeyresa (stała jest cena z okresu podstawowego p0)
Indeksy agregatowe ilości
Paaschego (stała jest cena z okresu badanego pn)
Indeks agregatowy wartości
Agregatowe indeksy cen pokazują:
- jaki był wpływ zmiany cen towarów na zmianę wartości całego agregatu (przy założeniu stałych ilości towarów wchodzących w skład agregatu)
- jak przeciętnie (dla wszystkich towarów) zmieniały się ceny jednostkowe, przy założeniu stałych ilości towarów.
PRZYKŁAD
Posiłek studenta składa się z kanapki, soku, ciastka i kawy:
Rodzaj |
Ceny (w zł) |
Indeks cen |
|
|
Styczeń 2007 |
Czerwiec 2007 |
|
|
p0 |
pn |
pn / p0 |
Kanapka Sok Ciastko Kawa |
2,5 2 1 1 |
3 2,5 2 2,5 |
1,20 1,25 2,00 2,50 |
Razem |
6,5 |
10 |
X |
Prosty agregatowy indeks cen
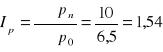
- oznacza, że koszt (wartość) posiłku wzrósł w czerwcu w stosunku do stycznia na skutek zmian cen o 54%.
PRZYKŁAD
W ciągu miesiąca student wypija 15 filiżanek kawy, 5 opakowań soku, zjada 10 kanapek i 5 ciastek.
Rodzaj |
p0 |
pn |
q0 |
pn / p0 |
p0 q0 |
pn q0 |
Kanapka Sok Ciastko Kawa |
2,5 2 1 1 |
3 2,5 2 2,5 |
10 5 5 15 |
1,20 1,25 2,00 2,50 |
25 10 5 15 |
30 12,5 10 37,5 |
Razem |
6,5 |
10 |
- |
6,95 |
55 |
90 |
Agregatowy indeks cen Laspeyresa
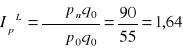
- oznacza, że ...
PRZYKŁAD
W badanym okresie nastąpiła nie tylko zmiana cen, ale również zmiana struktury spożywanych posiłków:
Rodzaj |
p0 |
pn |
q0 |
qn |
p0 q0 |
pn q0 |
p0 qn |
pn qn |
Kanapka Sok Ciastko Kawa |
2,5 2 1 1 |
3 2,5 2 2,5 |
10 5 5 15 |
10 10 8 8 |
25 10 5 15 |
30 12,5 10 37,5 |
25 20 8 8 |
30 25 16 20 |
Razem |
6,5 |
10 |
- |
- |
55 |
90 |
61 |
91 |
Agregatowy indeks cen Paaschego
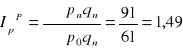
- oznacza, że ...
Podsumowanie:
Agregatowe indeksy cen obrazują dynamikę zmian wartości zespołu badanych artykułów na skutek zmian cen. Są one jednocześnie średnimi indeksów indywidualnych cen, a więc informują o przeciętnych zmianach cen poszczególnych składników w obu rozpatrywanych okresach.
Wyszukiwarka
Podobne podstrony:
Statystyka opisowa wykład interpretacje
Statystyka opisowa, Wykład 9, 4
Statystyka opisowa, Wykład 10, 4
STATYSTYKA OPISOWA 4 WYKŁAD 29.03.2009 doc, STATYSTYKA OPISOWA 4 WYKŁAD 29
Szereg rozdzielczy przedziałowy, Zarządzanie UWM, Statystyka opisowa
Najem Mieszkań, Zarządzanie UWM, Statystyka opisowa
Statystyka opisowa, Wykład 3
STATYSTYKA OPISOWA 5 WYKŁAD 25.04.2009, Statystyka opisowa i matematyczna, Statystyka opisowa i mate
STATYSTYKA OPISOWA 2 WYKŁAD 28. 02. 2009, Wykłady z wzorami.pl
STATYSTYKA OPISOWA WYKŁAD 3
zadania 1, Studia UEK Kraków Zarządzanie zaoczne, Statystyka opisowa
Statystyka opisowa, Wykład 4
Szereg rozdzielczy rodzeństwo studentów, Zarządzanie UWM, Statystyka opisowa
Wyjaśnienia, Zarządzanie UWM, Statystyka opisowa
STATYSTYKA OPISOWA WYKŁAD 9 (dekompozycja szeregu czasowego), statystyka
więcej podobnych podstron