Zagadnienia Egzaminacyjne 2013

http://www.asimo.pl/teoria.php

1. Robot

Mechaniczne urządzenie wykonujące automatycznie pewne zadania. Działanie robota może być sterowane przez człowieka, przez wprowadzony wcześniej program, bądź przez zbiór ogólnych reguł, które zostają przełożone na działanie robota przy pomocy technik sztucznej inteligencji. Roboty często zastępują człowieka przy monotonnych, złożonych z powtarzających się kroków czynnościach, które mogą wykonywać znacznie szybciej od ludzi. Domeną ich zastosowań są też te zadania, które są niebezpieczne dla człowieka, na przykład związane z manipulacją szkodliwymi dla zdrowia substancjami lub przebywaniem w nieprzyjaznym środowisku.

Pojęcia robot używamy też do nazywania autonomicznie działających urządzeń odbierających informacje z otoczenia przy pomocy sensorów i wpływających na nie przy pomocy efektorów.

Robot jest też ogólnym pojęciem stosowanym do określenia istniejących w rzeczywistości, bądź wyimaginowanych automatów i maszyn przypominających wyglądem człowieka lub zwierzę.

2. Robot przemysłowy

Manipulacyjny robot przemysłowy jest automatycznie sterowaną, programowaną, wielozadaniową maszyną manipulacyjną o wielu stopniach swobody, posiadającą właściwości manipulacyjne lub lokomocyjne, stacjonarną lub mobilną, dla ważnych zastosowań przemysłowych

Roboty przemysłowe stosuje się w celu zastąpienia ludzi w pracy na stanowiskach uciążliwych i niebezpiecznych. Najczęściej wykonują one zadania ryzykowne (np. obsługa prasy lub praca w środowisku agresywnym chemicznie), monotonne (np. obsługa taśmy produkcyjnej), czy wymagające dużej siły fizycznej (np. rozładunek, załadunek), bądź wyjątkowej precyzji (np. zaawansowana obróbka materiałowa).

3. Robotyka

jest dziedziną nauki zajmującą się wszystkimi problemami dotyczącymi mechaniki, sterowania ruchem, sensoryki, inteligencji maszynowej, projektowania, zastosowań i eksploatacji manipulatorów, robotów i maszyn kroczących.

4. Bionika

nauka badająca budowę i zasady działania organizmów oraz ich adaptowanie w technice (zwłaszcza w automatyce) i budowie urządzeń technicznych na wzór organizmu. Stara się poznawać i wykorzystać procesy sterujące działaniem organizmów w różnych działach techniki, głównie w automatyce, elektronice i mechanice. Patenty przygotowane przez naukowców wykorzystują rozwiązania występujące w naturze.

Przykłady biomimetyki w inżynierii zawierają kadłuby łodzi imitujących grubą skórę delfinów, sonar, radar, w medycynie ultradźwięki imitujące głos nietoperzy. W dziedzinie informatyki badania biomimetyki znalazły zastosowanie w cybernetyce, sztucznych neuronach, sztucznych sieciach oraz w miniaturyzacji krzemowych podzespołów na wzór naturalnych neuronów.

5. Prawa Robotyki Assimova

Celem tych praw było uregulowanie kwestii stosunków pomiędzy przyszłymi myślącymi maszynami a ludźmi. Przedstawiały się one następująco :

• 1. Robot nie może skrzywdzić człowieka, ani przez zaniechanie działania dopuścić, aby człowiek doznał krzywdy.

• 2. Robot musi być posłuszny rozkazom człowieka, chyba że stoją one w sprzeczności z Pierwszym Prawem.

• 3. Robot musi chronić sam siebie, jeśli tylko nie stoi to w sprzeczności z Pierwszym lub Drugim Prawem.

• 0. (prawo nadrzędne) Robot nie może skrzywdzić ludzkości, lub poprzez zaniechanie działania doprowadzić do uszczerbku dla ludzkości.

6. Funkcja skleronomiczne i reonomiczne

7. Funkcja holonomiczne i nieholonomiczne

8. Pozycjonowanie

Kalibracja to ogół czynności ustalających relację między wartościami wielkości mierzonej wskazanymi przez przyrząd pomiarowy a odpowiednimi wartościami wielkości fizycznych, realizowanymi przez wzorzec jednostki miary wraz z podaniem niepewności tego pomiaru.

W najprostszym przypadku polega to na określeniu różnicy pomiędzy wskazaniem przyrządu wzorcowego a wskazaniem przyrządu wzorcowanego z uwzględnieniem niepewności pomiaru dokonanego przy pomocy przyrządu wzorcowego.

Na dokładność manipulatora wpływają:

- błędy obliczeniowe

- dokładność obróbki poszczególnych elementów konstrukcyjnych

- elastyczność poszczególnych członów

- luzy w przekładniach

- oraz wiele innych elementów statycznych i dynamicznych

9. Zadanie proste

Proste zadanie kinematyki jest to zadanie statyczno-geometryczne polegające na obliczeniu pozycji i orientacji członu roboczego manipulatora. Mając dane wszystkie współrzędne konfiguracyjne należy obliczyć pozycję danego punktu związanego z robotem (przede wszystkim chwytaka) względem globalnego układu współrzędnych. Zadanie to traktujemy jako zadanie odwzorowania opisu położenia manipulatora w przestrzeni współrzędnych konfiguracyjnych na opis w przestrzeni współrzędnych kartezjańskiej.

10. Zadanie odwrotne

Odwrotne zadanie kinematyki polega na wyznaczeniu wszystkich możliwych zbiorów wartości przemieszczeń kątowych i liniowych (współrzędnych konfiguracyjnych) w połączeniach ruchowych, które umożliwią manipulatorowi osiągnięcie zadanych pozycji lub orientacji członu roboczego chwytaka lub narzędzia. Jest to podstawowe zadanie programowania i sterowania ruchu manipulatora, gdy trzeba znaleźć jak poszczególne współrzędne konfiguracyjne powinny zmieniać się w czasie w celu realizacji pożądanego ruchu członu roboczego.

Mając dane pozycję i orientację należy obliczyć wszystkie możliwe zbiory współrzędnych konfiguracyjnych tak, aby osiągnąć pożądaną pozycję i orientację. Jest to zadanie trudniejsze do prostego zadania kinematyki ze względu na wielokrotność rozwiązań i ich nieliniowość.

11. Konfiguracje robotów przemysłowych (równania)

12. Konfiguracja SCARA

http://www.robotyka.com/teoria/grafika/image072.gif

Konfiguracja SCARA (Selective Compliant Articulated Robot for Assembly), obecnie jedna z często występujących struktur w przemyśle

Głównym przeznaczeniem tej klasy manipulatorów jest montaż elementów i podzespołów oraz powtarzalne przenoszenie detali oraz ich sortowanie. Strukturę tę również wykorzystuje się do tworzenia obwodów drukowanych w elektronice. SCARA posiadając strukturę (OOP), różni się od konfiguracji sferycznej wyglądem jak i obszarem zastosowania.

13. Określenie „Denavita-Hartenberga”

Notacja Denavita-Hartenberga wprowadzona została do robotyki w celu uproszczenia opisu "mechanicznych ramion". W uproszczeniu przedstawia ona sposób na przejście od początku do końca układu połączonych ze sobą obiektów (które mogą być liniami prostymi, prostopadłościanami, itp.)

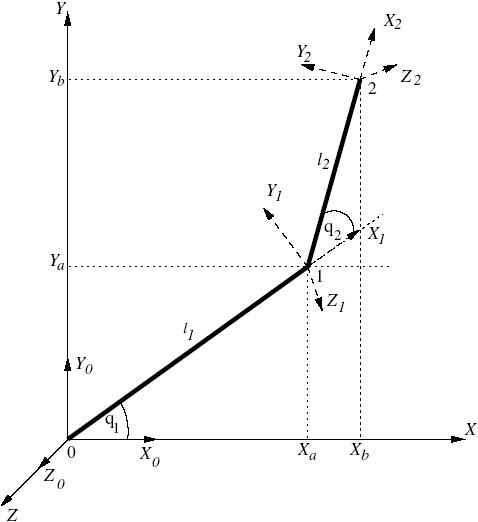
Przykład:

Na rysunku przedstawione zostało podwójne wahadło. Notacja Denavita-Hartenberga pozwala opisać sposób przemieszczenia się z punktu zaczepienia pierwszego wahadła (punktu 0), do punktu zaczepienia drugiego ramienia (punktu 1). W notacji Denavita-Hartenberga przedstawia się to jako:

gdzie:

RotZ oraz TrX są symbolami macierzy transformacji elementarnych,

q1,q2 określają kąt o jaki obrócone są wahadła,

l1,l2 są długością wahadeł.

Notacja ta pozwala za pomocą macierzy przedstawić algorytm przemieszczenia, umożliwiający wyznaczenie zależności położenia punktu końcowego od położenia punktów pośrednich.

/

14. Cosinus kierunkowy prostej

15. Trochoida

Trochoida (gr. trochós - koło, eídos - kształt) - krzywa płaska zakreślona przez dowolnie obrany punkt P stale związany z kołem O toczącym się wzdłuż wewnętrznej lub zewnętrznej strony stałego (nie poruszającego się) okręgu bez poślizgu. Termin został wprowadzony do matematyki przez Gilles'a de Robervala.

Jeśli punkt P pokrywa się ze środkiem toczącego się koła, wówczas poruszając się zakreśla okrąg. W pozostałych przypadkach tor ruchu P to krzywa (trochoida).

16. Jakobian

Macierz Jacobiego - macierz zbudowana z pochodnych cząstkowych (pierwszego rzędu) funkcji, której składowymi są funkcje rzeczywiste. Nazwa pojęcia pochodzi od nazwiska niemieckiego matematyka Carla Gustawa Jacobiego, który je wprowadził (niezależnie pojęcie to badał Michaił Ostrogradski).

Macierz Jacobiego i jej wyznacznik, nazywany jakobianem, znajdują zastosowanie w teorii funkcji uwikłanych, a także zagadnieniach związanych z zamianą zmiennych w całkach wielokrotnych, gdyż opisują one pochodną Frécheta funkcji wielu zmiennych (przestrzeni euklidesowych) w danym punkcie, o ile istnieje.

17. Tarcie

Tarcie (pojęcie fizyczne, jeden z oporów ruchu) to całość zjawisk fizycznych towarzyszących przemieszczaniu się względem siebie dwóch ciał fizycznych (tarcie zewnętrzne) lub elementów tego samego ciała (tarcie wewnętrzne) i powodujących rozpraszanie energii podczas ruchu.

Tarcie zewnętrzne występuje na granicy dwóch ciał stałych. Tarcie wewnętrzne występuje przy przepływie płynów, jak i deformacji ciał stałych.

Siła występująca w zjawiskach tarcia nazywana jest siłą tarcia.

18. Opory ruchu

Oporami ruchu nazywamy wszystkie siły działające na poruszające się ciało fizyczne, które przeciwdziałają poruszaniu się tego ciała.

19. Roboty kroczące

Wśród istniejących maszyn kroczących dostrzec można rozmaitość form i rozwiązań technicznych. Od konstrukcji jednonogich (monopodów), poprzez dwunożne (bipedy), czworonożne (quadropedy) do sześcionożnych (heksapody) i więcej nożnych, od stabilnie i twardo stąpających po ziemi (ze statyczną stabilnością) aż do podskakujących (z dynamiczną stabilnością)

Klasyfikacja robotów kroczących może być różna w zależności od obranego kryterium, jak liczba nóg, typ chodu, typ stabilności chodu, wzorzec ruchu. Niektóre z kryteriów są ze sobą ściśle powiązane, np. liczba nóg skorelowana jest z możliwymi rodzajami chodu. Do zalet maszyn kroczących można zaliczyć:

• adaptację i manewrowalność w zróżnicowanym (nierównym) terenie

• możliwość pokonywania przeszkód (dziury, nierówności)

• możliwość manipulowania obiektami za pomocą kończyn (np. owady).

Wśród wad maszyn kroczących najczęściej wymienia się:

• skomplikowana budowa mechaniczna (duża liczba stopni swobody)

• duże zapotrzebowanie na energię (wiele napędów)

• złożony układ sterowania.

Kolejnym kryterium oceny jakości robota kroczącego jest rodzaj stabilności. Wiąże się ona bezpośrednio z liczbą nóg. Rozróżnia się następujące rodzaje stabilności chodu:

• chód stabilny statycznie

• chód stabilny dynamicznie

• chód quasi-statycznie stabilny.

20. Kryteria stabilności

Stabilność układu - niezbędny warunek pracy układu automatycznej regulacji mówiący o tym, że układ po wyprowadzeniu go ze stanu równowagi sam powraca do tego stanu.

1. Kryterium biegunów

Wszystkie pierwiastki równania charakterystycznego układu zamkniętego powinny być ujemne, czyli znajdować się w lewej półpłaszczyźnie.

2. Kryterium odpowiedzi skokowej

Układ zamknięty w odpowiedzi na skok jednostkowy powinien osiągać stan ustalony w czasie dążącym do nieskonczoności.

3. Kryterium Hurwitza

Pierwiastki równania charakterystycznego układu zamkniętego będą znajdować się w lewej półpłaszczyźnie (układ będzie stabilny), jeśli spełnione zostaną 2 warunki:

a) Wszystkie współczynniki równania charakterystycznego muszą istnieć i mieć ten sam znak

b) Wszystkie podwyznaczniki wyznacznika głównego (posiadającego n wierszy i n kolumn) muszą być większe od 0

4. Kryterium Michajłowa

Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki w lewej półpłaszczyźnie, jeśli przyrost argumentu równania charakterystycznego w postaci widmowej przy zmianie pulsacji od 0 do wynosi , gdzie n jest stopniem równania.

5. Kryterium Nyquista

Układ zamknięty jest stabilny, jeżeli charakterystyka amplitudowo-fazowa układu otwartego nie obejmuje punktu (-1,j0).

6. Kryterium logarytmiczne Nyquista

Układ zamknięty jest stabilny, jeżeli logarytmiczna charakterystyka amplitudowa układu otwartego posiada wartość ujemną dla pulsacji odpowiadającej przesunięciu fazowemu .

21. Stopnie swobody

Liczbę niezależnych zmiennych opisujących jednoznacznie stan (modelu) układu fizycznego nazywa się liczbą stopni swobody tego układu.

W mechanice klasycznej jest to liczba niezależnych ruchów, jakie ciało jest w stanie zrealizować w przestrzeni. Przez niezależnych rozumie się, że żaden z tych ruchów nie może być uzyskany poprzez superpozycję pozostałych.

http://www.asimo.pl/teoria/stopnieswobody.php

22. Liczba Frouda

Liczba Frouda (własc. liczba Froude'a) - jedna z liczb podobieństwa, opisująca wpływ siły ciężkości na zjawiska przepływu płynów.

Liczba Frouda określa stosunek energii kinetycznej cieczy do energii potencjalnej potrzebnej do odchylenia (wymuszenia) przepływu płynów (cieczy lub gazu).

v - prędkość przepływu płynu;

g - przyspieszenie ziemskie;

L - wymiar liniowy.

23. Rodzaje sterowania robotów

Sterowanie (regulacja) polega na takim oddziaływaniu na obiekt sterowania, za pomocą sygnałów wejściowych, aby jego sygnały wyjściowe osiągneły pożądaną wartość.

Sterowanie może być realizowane przy pomocy człowieka - sterowanie ręczne lub za pomocą specjalnie skonstruowanego urządzenia (regulatora) - sterowanie automatyczne.

Sterowanie może odbywać się w układzie otwartym lub zamkniętym.

Sterowanie w układzie otwartym (ręczne lub automatyczne) polega na takim nastawie wielkości wejściowej, aby znając charakterystykę obiektu i przewidując mozliwość działania nań zakłóceń, otrzymać na wyjściu pożądaną wartość.

Sterowanie w układzie zamkniętym (ręczne lub automatyczne) różni się od sterowania w układzie otwartym tym, że człowiek lub regulator otrzymują dodatkowo poprzez sprzężenie zwrotne informacje o stanie wielkości wyjściowej. Informacja ta (odczytana z miernika lub podana w postaci np. napięcia do regulatora) jest używana do korygowania nastawu wielkości wejściowej.

24. Rodzaje programowania robotów:

Play Back:

•Ręczne przemieszczanie narzędzia zamocowanego w robocie po przewidzianym

torze ruchu

•Zapamiętanie współrzędnych punktów toru wszystkich osi ruchu

Teach in:

•Ustawienie robota w kolejnych pozycjach , zapamiętanie współrzędnych torów

punktów

•Odtwarzanie ich w zadanej kolejności z zadanymi, parametrami (prędkość ruchu,

rodzaj interpolacji

Języki wysokiego rzędu:

•Utworzenie programu pracy robota w języku wysokiego poziomu (podobnie jak w

przypadku OSN)

•Język specjalizowany zależny od producenta robota

Interaktywne programowanie graficzne:

•Wykorzystanie wirtualnej rzeczywistości w której jest zamodelowane całe

stanowisko robocze z poruszającym się robotem

•Projektowanie przemieszczeń (on line lub off -line)

---