LABORATORIUM FIZYKI I			Ćwiczenie nr: 1
						Data: 3.10.08
Wydział: SiMR	Grupa: 2.3	Zespół: 4	Punktacja:	Przygotowanie:
Nazwisko i Imię: Tomasz Demidowski
Temat ćwiczenia: Badanie korelacji liniowej pomiędzy prądem i napięciem					Sprawozdanie:
Prowadzący:					Suma punktów:

1. Wstęp

Celem ćwiczenia jest wyznaczenie nieznanej wartości rezystancji wewnętrznej rezystora, wykorzystując zależność prądu płynącego przez ten rezystor od napięcia odkładającego się na nim. Wyznaczenie szukanej wartości jest możliwe przy zastosowania prawa Ohma zadanego wzorem:

Dla używanego w badaniu układu (opisanego poniżej) prawo Ohma przyjmuję postać:

Natomiast wartość
określona jest zależnością:

Zatem
jest proporcjonalne do stosunku Rx/Rv. wartość mierzonej rezystancji Rx jest dużo mniejsza niż wartość rezystancji woltomierza Rv, dlatego wartość prądu płynącego przez woltomierz I_v jest pomijalnie mała. do obliczenia szukanej wartości wystarczą nam wartości napięcia zmierzonego woltomierzem i wartość prądu przepływająca przez amperomierz. Wspomniane wartości otrzymamy z przeprowadzonych pomiarów.

2. Układ pomiarowy

W ćwiczeniu wykorzystaliśmy następujący układ pomiarowy:

Układ pomiarowy składa się z :zasilacza, amperomierza, woltomierza i rezystora o nieznanej rezystancji, którą należy wyznaczyć. W obwodzie amperomierz został podłączony szeregowo, natomiast woltomierz równolegle. Zastosowaliśmy amperomierz o klasie dokładności 1% i zakresie pomiarowym 0,01 A oraz 0,03 A oraz woltomierz o klasie 1,5% i zakresie pomiarowym 5V i 15 V.

3. Wykonanie ćwiczenia

1. Podłączenie zgodnie ze schematem układu pomiarowego.

2. Ustawienie pokrętła zasilacza w położenie minimalnego napięcia wyjściowego.

3. Ustawienie zakresu amperomierza na 0,01 A, a woltomierza na 5V.

4. Włączenie zasilacza i ustawienie napięcia na 1V.

5. Odczytanie wartości natężenia pradu i zanotowanie.

6. kolejny pomiar dla 2V.

7. Zmiana zakresu pomiarowego amperomierza z 0,01A na 0,03A, ponieważ przy napięciu 3V wartość prądu przekraczała zakres pomiarowy.

8. Wykonanie kolejnych pomiarów

9. Zmiana zakresu pomiarowego woltomierza z 5V na 15 V przy dokonywaniu ostatniego pomiaru (6V).

4. Wyniki i ich opracowanie.

Pomiar	U[V]	I[A]	R[]
1.	1		232,5581
2.	2		263,1579
3.	3		270,2702
4.	4		277,7777
5.	5		287,3563
6.	6		294,1176

Pomiar	U[V]	I[A]	R[]
1.	1	0,0043	232,558	0,175	0,0002	51,514
2.	2	0,0076	263,158	0,175	0,0002	29,952
3.	3	0,0111	270,27	0,175	0,0006	30,375
4.	4	0,0144	277,778	0,175	0,0006	23,727
5.	5	0,0174	287,356	0,175	0,0006	19,966
6.	6	0,0204	294,118	0,325	0,0006	24,582

Do obliczenia wartości rezystancji skorzystaliśmy z prawa Ohma opisanego wzorem:

dla 3 pomiaru:

5. Rachunek błędów

1. Wyznaczenie błędu systematycznego pomiaru natężenia:

Klasa dokładności amperomierza: 1%

a)

Zakres 0,01A

[A]

b)

zakres 0,03A

[A]

2. Wyznaczenie błędu systematycznego pomiaru napięcia:

Klasa woltomierza: 1,5%

a)

Zakres 5V

[V]

b)

Zakres 15V

[V]

3. Wyznaczenie błędu rezystancji

Rezystancje obliczamy korzystając z wzoru (Prawo Ohma), dlatego błąd wyznaczmy korzystając z różniczki zupełnej (błąd wielkości wyznaczonej pośrednio).

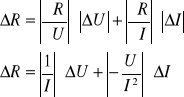
Dla 3 pomiaru:

I=
[A]

U=3 [V]

= 0,175 [V]

=
[A]

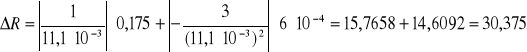
Nastepnie korzystając z metody najmniejszej sumy kwadratów wyznaczę prostą

dla której suma kwadratów odległości punktów pomiarowych od tej prostej jest najmniejsza, czyli prosta lezy najbliżej punktów pomiarowych. Do obliczeń wykorzystaliśmy program ORIGIN. Program ten wykorzystuje równanie prostej w postaci Y=A + BX do obliczenia parametrów dopasowania liniowego. W naszym przypadku mamy do czynie zależnością (prawem Ohma) opisana wzorem :

Przekształcając to równanie tak aby mialo charakter liniowy otrzymujemy:

Gdzie rezystancja R będzie współczynnikiem kierunkowym B.

Wykres został sporządzony na dołączonej kartce.

W naszym przypadku otrzymaliśmy następujące wyniki:

B=308,89576

A=-0,37149

Średni bład kwadratowy E_A (bład przypadkowy)=0,06499

Średni bład kwadratowy E_B (bład przypadkowy =4,7447

Program ORIGIN oblicza średni bład kwadratowy bez uwzględnienia współczynnika t-Studenta, dlatego aby uzyskać prawidłowa wartośc należy pomnożyć średni bład kwadratowy przez współczynnik t(
,k). w naszym przypadku:

k=n-2

Gdzie: n - liczba pomiarów

k=6-2=4

przyjmujemy, że współczynnik ufności
0,9, zatem t(
=0.9, k=4)=2,13

czyli błąd przypadkowy
:

Największy bład systematyczny dla obliczenia rezystancji wynosi

, tak więc błąd systematyczny jest porównywalny do błędu przypadkowego. W takiej sytuacji korzysta się z metody przenoszenia błedu.

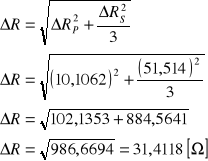
Ostatecznie wartość szukanej rezystancji wynosi:

Wnioski:

1. Celem ćwiczenia było wyznaczenie nieznanej wartości rezystancji. Po dokonaniu 6 pomiarów, dla różnych wartości napięcia i natęznia pradu uzyskaliśmy wynik
   

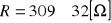
2. Jak widać powyższy wynik obarczony jest pewnym błedem. Wynika on w głównej mierze z błędow systematycznych związanych z dokonywaniem pomiarów, oraz koniecznością użycia metody pośredniej do wyznaczenia wartości rezystancji.

3. Przedstawiona metoda nie jest zbyt dokładna gdyż wartość błędu względnego jest stosunkowa duża i sięga około 10%

4. Jeden ze sposobów poprawienia dokładności pomiarów, mógłoby być kilkukrotne wykonywanie pomiarów natężenia dla ustalonej wartości napięcia. Mogłoby to wyeliminować niedokładności związane niepoprawnym odczytem wartości, które w przypadku jednokrtonytch pomiarów mogą mieć duży wpływ na wartość błędu pomiarowego.

Odpowiedź na pytanie 12:

a) Podczas przepływu pradu przez rezystor, będzie się zwiększac jego temperatura. Wynika to z prawa Joule'a - Lenza w myśl, którego ilość wydzielanego ciepła na rezystorze jest wprost

proporcjonalna do kwadratu natężenia pradu przez niego przepływającego (Q_c = RI²t).

---