Imię i nazwisko:	Ćwiczenie nr C1 Wyznaczanie ciepła topnienia lodu metodą kalorymetryczną.
Kierunek i rok:	Ocena z kolokwium: ....................................... data ....................... podpis...........................	Ocena ze sprawozdania: ....................................... data ....................... podpis...........................	Ocena końcowa: ....................................... data ....................... podpis...........................
Nazwisko prowadzącego zajęcia:

Molekularno-kinetyczna teoria budowy materii.

Rozwój atomistyki chemicznej dał dalszy impuls rozwojowi molekularno-kinetycznej teorii budowy materii, jednakże teoria kinetyczna gazów zaczęła rozwijać się już w XVIII wieku.

* Kinetyczna teoria gazów:

Najwcześniej rozwinęła się kinetyczna teoria gazów, gdyż gazy podlegają najprostszym prawom i pojęcie drobiny daje się dla nich dokładnie określić. W najprostszej swej postaci teoria kinetyczna gazów zakłada, że składają się one z bardzo małych drobin ożywionych nieustannym bezładnym ruchem. W przypadku gazów doskonałych teoria kinetyczna w najprostszej postaci zakłada, że drobiny gazu można uważać za sprężyste kulki, działające na siebie tylko w chwili zderzenia. Ciśnienie gazu wywołane jest przez nieustanne uderzenia drobin gazu o ścianki naczynia (Bernoulli).

Na poparcie poglądu o nieustannym ruchu drobin gazu można przytoczyć następujące fakty:

1. Gazy wypełniają całą dostępną im przestrzeń,

2. Istnienie w gazach zjawiska dyfuzji.

Najlepszy jednak i najbardziej bezpośredni dowód rzeczywistego istnienia bezładnego ruchu drobin stanowią tzw. ruchy Browna.

Na przełomie XVIII wieku M. Łomonosow wyraził pogląd, że ciepło polega na ruchu drobin; miał on wówczas na myśli ruchy obrotowe. Poglądy Łomonosowa nie znalazły uznania; kinetyczna teoria ciepła rozwinęła się dopiero w wieku XIX, po wykryciu równoważności ciepła i pracy oraz po sformułowaniu ogólnej zasady zachowania energii.

Z punktu widzenia kinetycznej teorii gazów energia cieplna gazu doskonałego, czyli jego energia wewnętrzna, jest po prostu energia kinetyczną bezładnych ruchów cieplnych jego drobin.

Teoria kinetyczna gazów w bardzo prosty sposób tłumaczy ciśnienie wywierane przez gaz na ścianki naczynia: jest to wynik nieustannego bombardowania ścianek naczynia przez drobiny gazu. Ściślejsze pojęcie tej myśli pozwala obliczyć średnia prędkość ruchu cieplnego drobin.

Również takie zjawiska jak dyfuzja jednego gazu w głąb drugiego, lepkość gazów i przewodnictwo cieplne, znajdują całkowite wytłumaczenie na gruncie kinetycznej teorii gazów. Teoria ta pozwala nam dzisiaj w dużej mierze zrozumieć własności gazów rzeczywistych. Jeśli chodzi o te ostatnie, to dochodzą już do głosu indywidualne własności drobin różnych gazów, a przez wszystkim ich wzajemne na siebie oddziaływanie (siły międzycząsteczkowe).

Wpływ sił międzycząsteczkowych w gazach jest niewielki i ujawnia się on w wyrazie poprawkowym w równaniu Van der Waalsa. Siły te mają jednak główną cechę charakterystyczną bardzo szybki spadek wartości wraz ze wzrostem odległości drobin. Dzisiejsza teoria budowy atomów pozwala wyjaśnić naturę tzw. sił Van der Waalsa. Przy zbliżeniu do siebie dwóch atomów czy drobin występuje ich wzajemne polaryzowanie się. Atom składa się z dodatniego jądra i chmury ujemnych elektronów. Jeżeli zbliżmy do niego drugi atom, to elektrony drugiego atomu, które bardziej zbliżają się do pierwszego atomu niż jądro, wywierać będą siły odpychające na elektrony tego atomu, a przyciągające na jego jądro. W rezultacie jądro przesunie się w stronę przeciwna niż środek naboju chmury elektronowej (odpowiednik środka masy - punkt, w którym można umieścić nabój ujemny, zastępujący nabój chmury elektronowej). Atom pierwszy staje się więc dipolem elektrycznym; podobnie będzie i z atomem drugim. Takie dwa wymuszone dipole przyciągają się nawzajem siłą zmieniającą się odwrotnie proporcjonalnie do siódmej potęgi ich odległości, a więc bardzo szybko. Analogicznie będą się zachowywać drobiny.

Ta szybka zmienność sił Van der Waalsa wraz z odległością pozwala wprowadzić pojęcie sfery działania drobin czy atomu - bardzo pożytecznego przybliżenia dla opisu wzajemnych działań drobin na siebie. Sferą działania drobiny nazywać będziemy kulę zakreśloną dookoła środka drobiny tak, by siły Van der Waalsa między drobinami miały dostrzegalną wartość, jeśli środek drugiej drobiny znajdzie się w obrębie tej kuli, i by można było natomiast te siły zaniedbać, jeśli środek drugiej drobiny znajduje się na zewnątrz sfery działania. Ze względu na bardzo ostry spadek sił przyciągania międzydrobinowego wraz ze wzrostem odległości drobin, wartość promienia sfery działania zależy w dużym stopniu od tego, jaka obierzemy wartość siły, którą można zaniedbać, gdyż nieznaczna nawet zmiana odległości powoduje już dużą zmianę wartości siły.

* Teoria atomowa ciał stałych:

Jeśli chodzi ciała stałe, a więc w naszym rozumieniu ciała krystaliczne, to zrozumienie ich własności, z punktu widzenia teorii kinetycznej, poczyniło wielkie postępy dopiero w ostatnich pięćdziesięciu latach. O ile w teorii gazów duże uproszczenia wynikają z bezładnego ruchu ich drobin, o tyle w kryształach decyduje uporządkowanie ich podstawowych cegiełek: jonów, atomów czy drobin. Cegiełki te zajmują zupełnie określone, prawidłowo rozmieszczone położenie równowagi, tworzące siatkę krystaliczną. Dokoła tych położeń równowagi wykonują one drgania, tym silniejsze, im wyższa jest ich temperatura. Cegiełki te powiązane są ze sobą siłami międzydrobinowymi (a raczej najczęściej międzyjonowymi lub międzyatomowymi), które obejmujemy nazwa sił spójności; w zależności od typu kryształu siły te mogą mieć bardzo różny charakter. Gdy cegiełki te zostaną wyprowadzone z położeń równowagi jakimiś siłami zewnętrznymi, pojawiają się napięcia sprężyste, dążące do przywrócenia równowagi. Makroskopowo opisujemy napięcie przez wprowadzenie pewnych współczynników czy modułów sprężystości, charakterystycznych dla danego kryształu. Ale dopiero od niedawna postępy fizyki atomowej pozwoli przeprowadzić racjonalną klasyfikacje typów kryształów i dla niektórych kryształów - zwłaszcza dla kryształów jonowych - obliczyć nawet pewne wartości stałych makroskopowych, charakteryzujących kryształ.

Ostatnio rozwoju atomistycznej teorii ciał stałych coraz wyraźniej zarysowuje się wielkie znaczenie nieprawidłowości w budowie siatki krystalicznej, a więc nieprawidłowości mikrokrystalicznej budowy ciała, np. istnienia nieobsadzonych miejsc w siatce, obcych centrów w węzłach bądź pomiędzy węzłami siatki itp. Te nieprawidłowości mają zasadniczy wpływ na makroskopowe własności ciał stałych, a zwłaszcza na ich wytrzymałość i własności plastyczne. Ten dział fizyki ciała stałego bardzo szybko się dzisiaj rozwija i w niezbyt dalekiej przyszłości będzie miał niewątpliwie duże znaczenie dla rozwoju techniki.

* Teoria kinetyczna cieczy:

Najmniej stosunkowo poczyniła postępów teoria kinetyczna cieczy. W gazach drobiny są przeciętnie w tak dużych odległościach jedna od drugiej, że możemy je uważać za swobodne i mówić tylko o ich zderzeniach: mamy tu zupełny nieporządek. W ciałach stałych ich cegiełki stale na siebie oddziałują, co prowadzi do powstawania uporządkowanej sieci krystalicznej; mamy tu w pierwszym przybliżeniu zupełny porządek. W cieczach zaś jest sytuacja pośrednia. Drobiny cieczy znajdują się stale jedna w sferze działania drugiej, jednak oddziaływania te nie prowadzą do powstawania siatki krystalicznej. Mamy tu sytuację wyraźnie pośrednią pomiędzy gazem a ciałem stałym. Równanie Van der Waalsa podkreśla, że w temperaturze krytycznej mamy zupełnie ciągłe przejście miedzy cieczą a gazem. Jednakże w dużo niższych temperaturach zarysowują się pewne analogie między cieczą a ciałem krystalicznym; pojawiają się zaczątki uporządkowania drobin, możemy mówić o quasi-krystalicznej budowie cieczy. Ten przejściowy charakter cieczy powoduje duże trudności w systematycznym opracowaniu kinetycznej teorii cieczy i sprawia, że jest ona do dziś raczej w zaczątku.

Ciepło właściwe substancji c - stosunek ilości ciepła Q pobranego przez ciało do iloczynu masy m substancji i przyrostu jego temperatury ∆T wywołanego pobraniem tego ciepła:

Jednostką ciepła właściwego jest dżul na kilogram i kelwin:

.

Jest to ciepło właściwe ciała o masie 1 kg, którego temperatura wzrasta o 1 K po pobraniu przez nie ciepła w ilości 1 J.

Ciepło topnienia, q_t - stosunek ilości ciepła Q pobranego do stopienia ciała o masie m do jego masy przy stałym ciśnieniu i temperaturze:

Jednostką ciepła topnienia jest kaloria na gram:

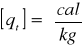
W miarę podnoszenia się temperatury słabną własności charakterystyczne dla ciała stałego, przede wszystkim sprężystość postaci i moduł Younga. Z punktu widzenia molekularnej teorii budowy materii wiążemy to z rozluźnieniem więzów między drobinami. W miarę wzrostu temperatury granica sprężystości ciała stałego obniża się coraz bardziej i ciało staje się coraz mniej plastyczne. Nie wszystkie ciała zachowują się tu jednakowo. Ciała takie jak szkło, twarde i kruche w zwykłej temperaturze, w miarę wzrostu temperatury stają się stopniowo mniej twarde i kruche, natomiast coraz bardziej plastyczne i w sposób całkowicie ciągły przechodzą wreszcie w ciecz. Podobnie zachowuje się np. wosk, smoła, masło, żywica itp. Są to wszystko ciała bezpostaciowe, to znaczy ciała, w których nawet prześwietlenie promieniami X nie wykazuje budowy mikrokrystalicznej. Ciała bezpostaciowe nie mają temperatury topnienia. Jeżeli ciało bezpostaciowe ogrzewamy, dostarczając mu równomiernie ciepła, temperatura jego rośnie w sposób ciągły i nieprzerwany. Jak widać z krzywej na poniższym rysunku:

r.3.1.s.67.

możemy tylko wyróżnić pewien obszar temperatury, w którym jej przyrost jest wyraźnie zwolniony. Dla ciał takich nie możemy mówić o określonej temperaturze topnienia.

Ciała krystaliczne zachowują się wyraźnie odmiennie. Krzywa ogrzewania ciał krystalicznych na przebieg pokazany na poniższym rysunku (krzywa topnienia lodu):

r.3.2.s.67.

obserwujemy tu przy równomiernym dopływie ciepła ustalenie się pewnej ściśle określonej temperatury, w której trwa topnienie, dopóki nie stopi się całkowita rozporządzalna ilość ciała stałego. Z tą chwilą dopiero rozpoczyna się dalszy wzrost temperatury. W związku z tym wprowadzamy pojecie ciepła topnienia, to znaczy ciepła zużytego na sama zmianę tylko stanu skupienia. Ciecz powstająca przy topieniu ma te samą temperaturę co ciało stałe. Wykres wskazuje wyraźnie, że z topnienie związane jest pochłanianie ciepła.

Szereg ciał pod wpływem ogrzewania może doznawać przemian wewnętrznych. W przypadku ciał krystalicznych zdarza się, ż e ciało występuje w dwóch lub więcej postaciach, tzw. odmianach alotropowych, różniących się budową kryształów. Tak np. siarka występuje w odmianie rombowej i w odmianie jednoskórnej. Przejście z jednej odmiany w drugą odbywa się w ściśle określonej temperaturze i ma charakter podobny do topnienia. Przemiana siarki z odmiany rombowej w jednoskórną pod normalnym ciśnieniem zachodzi w temperaturze 95,6 st. Celsjusza.

Jeszcze innego typu przeobrażenia wykazuje czyste żelazo ogrzewane do temperatury 768 st. Celsjusza. Traci ono wówczas nagle swoje własności magnetyczne, przy czym przy równomiernym dopływie ciepła następuje w sąsiedztwie tego punktu wyraźne zwolnienie szybkości wzrostu temperatury. W temperaturze tej nie zachodzą żadne zmiany budowy krystalicznej żelaza, nie mamy zatem tutaj do czynienia z przemianą alotropową. Chodzi tu o tzw. przemianę drugiego rodzaju, związaną ze skokiem wartości ciepła właściwego.

Jak już wspomniałam poprzedni, topnieniu towarzyszy pochłanianie ciepła, bez równoczesnej zmiany temperatury. Z tego tez powodu używano dawnej terminu utajone ciepło topnienia. Ciepłem topnienia nazywamy ilość ciepła potrzebną do zmiany 1g danego ciała stałego w cieczo tej samej temperaturze; wyrażamy je najczęściej w cal/g. W temperaturze topnienia mamy równowagę termiczną pomiędzy ciałem stałym a ciekłym. Ciepło topnienia wyznaczamy za pomocą kalorymetru. Jeśli np. chcemy wyznaczyć ciepło topnienia lodu, wrzucamy do kalorymetru m gramów lodu, którego temperatura wynosi 0 st. Celsjusza. Lód topnieje ostateczna temperatura wody w kalorymetrze wynosi t₁. Przypuśćmy, że pierwotnie w kalorymetrze było m_w gramów wody o temperaturze t₀; równoważnik wodny kalorymetru niech wynosi W. Ciepło pobrane przez lód i wodę powstającą po jego stopieniu jest równe:

c_x - ciepło topnienia lodu,

c_w - ciepło właściwe wody.

Ciepło Q₂ pobrane przez wodę i kalorymetr jest równe:

Ze względu na zasadę bilansu cieplnego przez porównanie znajdujemy:

Temperatura (empiryczna) - skalarna wielkość fizyczna charakteryzująca stan równowagi termicznej układu o tej własności: dwa ciała znajdują się w stanie równowagi termicznej wtedy i tylko wtedy, gdy ich temperatury są sobie równe. Wyznacza się ją za pomocą termometru.

Przyporządkowanie wartości temperatury danemu stanowi równowagi termicznej ciała wzorcowego, zwanego ciałem termometrycznym (np. określona ilość rtęci, spirytusu), przeprowadza się na podstawie mierzalnych własności zależnych od temperatury, tzw. cech termometrycznych (np. objętość cieczy, ciśnienie gazu). Wybranym punktom stałym ciała wzorcowego przypisuje się określone wartości temperatury i ustala się zależność (najczęściej liniową) między cechą termometryczną a temperatura. Powstaje w ten sposób empiryczna skala temperatury.

Skale temperatur:

* Skala Celsjusza, t - skala temperatury oparta na dwóch punktach stałych: 0 st. C - punkt topnienia lodu przy ciśnieniu normalnym 1013,25 hPa i 100 st. C - punkt wrzenia wody przy ciśnieniu normalnym. Jednostka temperatury w tej skali jest 1 stopień Celsjusza (1° C).

* Skala Fahrenheita, t_F - skala temperatury stosowana w krajach anglosaskich oparta początkowo na dwóch punktach stałych: 0 st. F - punkt topnienia mieszaniny śniegu i salmiaku i 100 st. F - normalna temperatura ciała ludzkiego. Obecnie skalę temperatury Fahrenheita definiuje się przez przyporządkowanie temperaturze 0° C wartości 32° F i temperaturze 100° C - wartości 212° F. Jednostką temperatury w tej skali jest 1 stopień Fahrenheita (1° F).

* Skala Kelvina (bezwzględna skala temperatury), T - skala temperatury niezależna od ciała wzorcowego, której wprowadzenie umożliwia II zasada termodynamiki, może być również zdefiniowana na podstawie własności gazu doskonałego. Do jej określenia wystarczy jeden punkt stały - jest nim punkt potrójny wody, któremu przypisano temperaturę (bezwzględną) T = 273,16 K. Jednostka temperatury w tej skali jest kelwin (1 K) - jednostka podstawowa w układzie SI.

Temperatura 0 K (temperatura zera bezwzględnego) jest najniższą temperaturą rozpatrywaną w fizyce klasycznej.

Porównanie skal temperatur:

p.228.

P_w - punkt wrzenia wody przy ciśnieniu normalnym,

P_t - punkt topnienia lodu przy ciśnieniu normalnym,

Z_b - zero bezwzględne.

Zależność temperatury od ciśnienia (pojęcie parowania).

Parowaniem nazywamy przejście ze stanu ciekłego w gazowy. Parowanie odbywa się w każdej temperaturze na powierzchni cieczy. Szybkość parowania zależy od temperatury i ciśnienia. Wzrost temperatury powoduje zwiększenie szybkości parowania wszystkich cieczy. Wzrost ciśnienia powoduje zmniejszenie szybkości parowania. Szybkość parowania zależy od warunków otoczenia. Przepływ powietrza (np. wiatr) usuwający gromadzącą się parę powoduje zwiększenie szybkości parowania.

Gdy przy danym ciśnieniu zewnętrznym podwyższymy temperaturę cieczy, to w pewnej określonej temperaturze charakter parowania ulega wyraźnej zmianie. Pęcherzyki pary zaczynają tworzyć się nie tylko na powierzchni ale i we wnętrzu cieczy oraz na ściankach naczynia zawierającego ciecz. Cała ciecz zostaje wprawiona w burzliwy ruch, rozpoczyna się wrzenie.

Wrzenie możemy wywołać przy niższej temperaturze, np. w temperaturze pokojowej przez odpowiednie obniżenie ciśnienia. Utrzymanie cieczy w stanie ciekłym w pewnej temperaturze jest możliwe tylko przy dostatecznie wielkim ciśnieniu zewnętrznym. Jeśli ciśnienie zewnętrzne jest mniejsze od tego ciśnienia, rozpoczyna się gwałtowne wrzenie. Tak np. woda w temperaturze 100°C pozostaje w stanie ciekłym tylko pod ciśnieniem nie mniejszym od l at. W temperaturze 374°C woda wymaga ponad 200 at ciśnienia, by pozostać w stanie ciekłym. Istnieją ciecze, np. bezwodnik węglowy, które już w pokojowej temperaturze wymagają ciśnienia większego od l atmosfery, aby utrzymać się w stanie ciekłym. Ciecze takie nie mogą pozostawać w naczyniu otwartym, gdyż wówczas stale wrą. Jeśli natomiast ciecze w temperaturze pokojowej wrą pod ciśnieniem mniejszym od atmosferycznego, można je doprowadzić do wrzenia pod ciśnieniem atmosferycznym przez odpowiednie podwyższenie temperatury.

Pod ciśnieniem atmosferycznym każda ciecz wrze w zupełnie określonej temperaturze. Jak widać z porównania danych liczbowych podanych w tablicach nie istnieje związek między temperatura topnienia a temperaturą wrzenia pod ciśnieniem stałym.

Tabela wyników pomiarów nr 1:

Lp.	m1=mk+mw [kg]	ck* [J/kg·K]	mk [kg]	cw** [J/kg·K]	mw [kg]	T0 [K]	T1 [K]	T2 [K]	∆T [K]	m2=m1+ml [kg]	ml [kg]
1	0,2572	896	0,0946	4186	0,1626	273	296,0	286,0	10,0	0,2772	0,0200
2	0,2645	896	0,0946	4186	0,1699	273	293,0	278,5	14,5	0,3001	0,0356
3	0,3204	896	0,0946	4186	0,2258	273	305,5	290,5	15,0	0,3557	0,0353
4	0,3439	896	0,0946	4186	0,2493	273	298,5	286,5	12,0	0,3753	0,0314

* Ciepło właściwe kalorymetru (ciepło właściwe glinu) - wartość tablicowa - „I pracownia fizyczna“ S. Szczeniowski, 1975 r.

** Ciepło właściwe wody - wartość tablicowa - „I pracownia fizyczna“ S. Szczeniowski, 1975 r.

∆m = ± 0,00005 kg

∆T = ± 0,25 K

Wyznaczam ciepło topnienia lodu dla poszczególnych pomiarów:

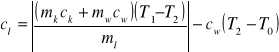
Pomiar 1: c_l = 328284,6000 [J/kg]

Pomiar 2: c_l = 301175,4129 [J/kg]

Pomiar 3: c_l = 364405,2266 [J/kg]

Pomiar 4: c_l = 374698,4522 [J/kg]

Wyznaczam niepewności ciepła topnienia lodu metodą różniczki zupełnej:

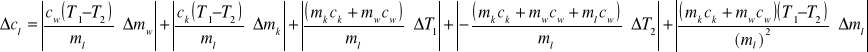
Pomiar 1: ∆c_l = ± 21265,4365 [J/kg]

Pomiar 2: ∆c_l = ± 12784,58625 [J/kg]

Pomiar 3: ∆c_l = ± 16363,06406 [J/kg]

Pomiar 4: ∆c_l = ± 19167,88872 [J/kg]

Wyznaczam niepewności procentowe pomiarów:

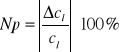
Pomiar 1: Np = ± 6,5%

Pomiar 2: Np = ± 4,24%

Pomiar 3: Np = ± 4,5%

Pomiar 4: Np = ± 5,12%

Wyznaczam średnią wartość ciepła topnienia lodu (średnia ważona):

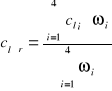
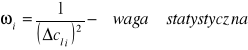
c_lśr = 334734,6613 [J/kg]

Wyznaczam średnią niepewność ciepła topnienia lodu (średnia ważona):

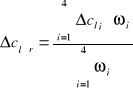
∆ c_lśr = ± 16131,82127 [J/kg]

Wyznaczam średnią niepewność procentową:

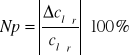
Np = ± 4,82%

Tabela wyników pomiarów nr 2 (zależność temperatury od czasu):

	t [s]	30	60	90	120	150	180	210	240	270	300
Numer pomiaru		T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]
2		289	287	285	284	282,5	282	281	280,5	280	280
3		303	301	298	296,5	294,5	292	291	290,5	290,5	290,5
4		296,5	295	293	291,5	290	289	288	287,5	287,5	287
	t [s]	330	360	390	420	450	480	510	540	570	600
Numer pomiaru		T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]
2		280	279	279	279	279	279	278,5	278,5	278,5	278,5
3		290,5	290,5	290,5	290,5	290,5	290,5	290,5	290,5	290,5	290,5
4		287	286,5	286,5	286,5	286,5	286,5	287	287	287	287
	t [s]	630	660	690	720	750	780	810	840	870	900
Numer pomiaru		T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]	T [K]
2		278,5	278,5	278,5	278,5	278,5	278,5	279	279	279	279
3		290,5	290,5	290,5	290,5	290,5	290,5	291	291	291	291
4		287	287	287	287	287	287	287	287	287	287,5

Co 30 s odczytywałam wartość temperatury T i dane te umieściłam w powyższej tabeli. Na jej podstawie wykonałam wykresy zależności temperatury podczas topnienia od czasu, w którym to topnienie następowało. Pierwszy pomiar był dokonany bez pomiaru temperatury co 30 s.

WNIOSKI I UWAGI:

Otrzymane wyniki:

Pomiar 1: c_l = (328284,6000 ± 21265,4365) [J/kg]

Pomiar 2: c_l = (301175,4129 ± 12784,58625) [J/kg],

Pomiar 3: c_l = (364405,2266 ± 16363,06406) [J/kg],

Pomiar 4: c_l = (374698,4522 ± 19167,88872) [J/kg],

porównałam z wartościami tablicowymi* (c_l = 332000 [J/kg]).

Różnice nie są rażąco duże, dlatego można uznać, że doświadczenia zostało przeprowadzone w prawidłowy sposób.

Różnice między wynikami moich pomiarów, a wartością tablicową mogą wynikać z niedokładności przeprowadzonych pomiarów, wad sprzętu (nieszczelności kalorymetru, co powodowałoby pobieranie ciepła z otoczenia, niedokładności wagi czy termometru), warunków otoczenia. Na dokładność pomiaru ciepła topnienia lodu wpływa dokładność pomiaru masy oraz temperatury. Do obliczeń zakładam, że wartość początkowa temperatury lodu wynosi 273 K, a tak nie musi być. Gdyby temperatura początkowa lodu była niższa niż 273 K, to lód do osiągnięcia zakładanej temperatury pobrałby już pewna ilość ciepła. A gdyby temperatura początkowa lodu była wyższa, to lód pobrałby mniejszą ilość ciepła z wody i szybciej by się topił. W moich pomiarach i obliczeniach nie zostały uwzględnione jakiekolwiek poprawki, co do temperatury początkowej lodu.

Można by zmniejszyć niepewności pomiarów, stosując bardziej dokładne urządzenia pomiarowe oraz uwzględniając temperaturę początkową lodu.

---