Pytania na statystykę które były kiedyś tam na egzaminach
1 czym jest cecha statystyczna, podaj typy cech oraz przykłady
Elementy populacji generalnej mogą mieć różne własności, które podlegają obserwacji i, które pozwalają na rozróżnianie elementów w populacji. Te własności nazywa się cechami statystycznymi lub krótko cechami.
Te własności które mają charakter ilościowy nazywa się cechami mierzalnymi (np. wzrost, waga).
Własności jakościowe jak płeć kolor włosów, nazywa się cechami niemierzalnymi.
Cechy statystyczne (mierzalne), które przyjmują wartości całkowite nazywa się cechami skokowymi lub dyskretnymi.
Cechy przyjmujące wartości rzeczywiste nazywa się cechami ciągłymi.
2 Różnica pomiędzy odchyleniem standardowym a wariancją
Wariancja-kwadrat odchylenia standardowego.
3 podaj wymagania dotyczące przedziałów klasowych przy budowie histogramu
-liczba przedziałów klasowych nie powinna być mniejsza niż7 i większa od15,
-liczebność w każdym przedziale nie powinna być mniejsza od 5,
-sposób określenia: m=1+3.3log(n)
m<5log(n)
4 wyjaśnij pojęcie populacji generalnej i próby.
Badanie statystyczne dotyczy zawsze pewnej zbiorowości, której elementami są obiekty materialne lub zjawiska. W statystyce matematycznej badaną zbiorowość statystyczną nazywa się populacją generalna lub zbiorowością generalną.
Próba jest to podzbiór populacji generalnej podlegających badaniu
5 Podaj wzór na średnią arytmetyczną średnią ważoną i odchylenie standardowe
1.
Średnia arytmetyczna ![]()
:
![]()
![]()
![]()
- średnia arytmetyczna zmiennej X
xi - wartości zmiennej X (i=1,2...n)
n - liczebność próby
Odchylenie standardowe jest to średnia kwadratowa odchyleń poszczególnych wartości zmiennej od ich średniej arytmetycznej
s =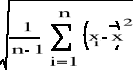

6 Róznica pomiędzy rozkładem normalnym a rozkładem normalnym a rozkładem normalnym standaryzowanym.
Przy rozkładzie normalnym standaryzowanym wartość średnia m=0 a odchylenie standardowe sigma=1 N(0,1). Przy rozkładzie normalnym N(m,sigma) m jest różne od 0.
7 współczynnik ufności i poziom istotności.
Współczynnik ufności `1-a'(w praktyce przyjmuje się `1-a>=0.9') i `a'
Poziom istotności to z góry ustalone małe prawdopodobieństwo `a' błędu pierwszego rodzaju
8 na czym polega weryfikacja hipotez statystycznych
1)Obliczenie parametrów z próby (wartość średnia)
2)Zakładamy prawdopodobieństwo alfa(tzw. Poziom ufności a<0.1
3)obliczamy na podstawie testu wartość testu Ro
4)obliczamy tzw obszar kryterialny Ra odrzuceń hipotez (na podstawie a)
5)porównujemy Ro i Ra
6)Przyjmujemy lub odrzucamy postawioną hipotezę
9 wymienić rozkłady zmiennej losowej dyskretnej i ciągłej
Rozkład ciągły: Rozkład normalny, normalny standaryzowany, wykładniczy, studenta, trójkątny, chi-kwadrat
Rozkład dyskretny: Rozkład dwumianowy Bernuliego, Poisona, jednopunktowy, dwupunktowy, równomierny.
10 co to jest histogram narysować i opisać dokładnie.
Histogram to jeden z graficznych sposobów przedstawienia rozkładu cechy. Składa się z szeregu prostokątów umieszczonych na osi wsp. Prostokąty te są z jednej strony wyznaczone przez przedziały klasowe wartości cechy (szereg rozdzielczy) a ich wysokość jest określona przez liczebności elementów wpadających do określonego przedziału klasowego.
Postępowanie podczas tworzenia histogramu:
1)uporządkowanie wartości (x min, x max)-szereg pozycyjny
2)R - Rozstęp (ile wartości jest w przedziałach)
R= x max- x max
3)zakładamy liczbę przedziałów klasowych n,
4)Liczymy długość przedziału d
d=R/n
11 Rodzaje hipotez statystycznych
Hipoteza statystyczna to każde przypuszczenie dotyczące wielkości parametru dotyczącej zmiennej losowej w populacji generalnej lub próbnej, albo też postaci tego rozkładu uzyskane na podstawie próby losowej.
-testy parametryczne(związane z wartościami parametrów),
-testy nieparametryczne(związane z postacią rozkładów)
12 Co to jest dystrybuanta
Dystrybuanta empiryczna ![]()
Dystrybuanta zmiennej losowej określa prawdopodobieństwo tego, że zmienna losowa X przyjmie jakąkolwiek wartość mniejszą od z góry przyjętej danej wartości xi
13 Przedział ufności (różnice miedzy współczynnikami) ??????????????
1)przedział ufności dla wartości średniej
Model1i 3
Wartość Ua dla danego współczynnika ufności 1-a wyznacza się z rozkładu normalnego standaryzowanego N(0,1), w taki sposób by była spełniona relacja
P{-ua<U<ua}=1-a
Model2
Wartość współczynnika ta oznacza wartość zmiennej t studenta odczytaną z tablic tego rozkładu dla n-1 stopni swobody dla zadanego z góry prawdopodobieństwa 1-a tak by była spełniona zależność:
P{-ta<t<ta}=1-a
Przedział ufności dla wariancji
Model 1
Współczynniki C1 i C2 są wartościami zmiennej chi-kwadrat wyznaczonymi dla n-1 stopni swobody oraz współczynnika ufności 1-a tak by były spełnione relacje:
P(X2 <C1)=(1/2)a
P(X2 =>C2) =(1/2)a
Model2
Współczynnik ua jest wartością zmiennej normalnej standaryzowanej U wyznaczony dla 1-a z tablic rozkładu normalnego by była spełniona relacja:
P{-ua<U<ua}=1-a
14 szereg rozdzielczy i pozycyjny.
Szereg pozycyjny- uporządkowanie liczb w kolejności od najmniejszej do największej
Szereg rozdzielczy-Gdy liczebność jest duża to najpierw tworzymy szereg pozycyjny a następnie grupujemy. Grupowanie polega na podzieleniu próby na podzbiory zwane grupami lub klasami. Wartościami reprezentującymi poszczególne klasy są ich środki oraz liczebności, tworząc razem szereg rozdzielczy
19przedział ufności
przedział ufności to taki przedział, który z dużym prawdopodobieństwem obejmuje prawdziwą wartość parametru. W zależności od przyjętych założeń otrzymuje się konkretne wzory na przedziały ufności, w oparciu o rozkład normalny lub t-Studenta
15 narysować krzywą Gaussa w rozkładzie normalnym z zaznaczonymi parametrami
16 co to jest metoda estymacji przedziałowej, opisać dokładnie
Estymacja przedziałowa to szacowanie w postaci przedziałów pewnych parametrów zmiennej losowej.
Przedział taki nazywamy przedziałem ufności
X-zmienna losowa(wzrost)
x - średni wzrost
Różnica pomiędzy s sigma
s- odchylenie standardowe z próby losowej
sigma - odchylenie standardowe dla całej populacji
Postępowanie podczas obliczeń:
1)obliczyć wartość średnią x
2)obliczyć s lub założyć sigmę
3)odczytać z tablicy kwantyle rozkładu Ua, ta, X2
4)ze wzorów obliczamy granicę przedziałów
17 testy nieparametryczne, opisać i przedstawić graficznie test zgodności
Dotyczą postaci rozkładów to znaczy weryfikuje się hipotezę o postaci funkcyjnej rozkładu populacji generalnej. Warunki przeprowadzenia
1)Można je stosować gdy liczebność próby jest duża(im liczebność jest duża tym wynik jest bardziej prawdopodobny) n>100
2)Zakładamy prawdopodobieństwo a które ma być małe ale nie mniejsze niż 0.01
3)Budowa histogramu(empiryczny rozkład cech) i porównujemy z rozkładem normalnym a następnie stawiamy hipotezę
5,7,13,18,11,8,5-liczebność w klasie(empiryczna)
n*f(x)-liczebność teoretyczna
Trzeba sprawdzić na ile histogram jest dopasowany do rozkładu normalnego
Obliczamy odległość histogramu od rozkładu normalnego
Oblicza się prawdopodobieństwo np. z Bernulliego
N*pi-liczebność teoretyczna (oczekiwana w tym przedziale)
18 Narysować rozkłady normalne N(0,0.1),N(0,1),N(0,10),N(-5,1),N(5,1)
19 wyznaczyć prawdopodobieństwo przyjęcia przez zmienną losową o rozkładzie chi-kwadrat o 18 stopniach swobody wartość x=8
Prawdopodobieństwo, że zmienna losowa (ciągła) przyjmie konkretne wartości jest równe zero(np.
4,3,2...).Prawdopodobieństwo od zmiennej losowej ciągłej liczymy tylko w przedziałach, gdyż zmienna losowa ciągła jest nieskończona.
20)czym jest hipoteza statystyczna(podać postać hipotez). Jaka jest różnica pomiędzy hipotezą zerową a alternatywną
Hipoteza statyczna to każde przypuszczenie dotyczące wielkości parametru rozkładu zmiennej losowej
W populacji generalnej lub próbnej, albo też postaci tego rozkładu uzyskane na podstawie próby losowej.
Zerowa- hipoteza którą weryfikujemy ,
Alternatywna-hipoteza którą przyjmujemy lub odrzucamy po zweryfikowaniu hipotezy zerowej
21) Zależność pomiędzy dystrybuantą a funkcją rozkładu prawdopodobieństwa
Dodając prawdopodobieństwa w odpowiednich przedziałach otrzymujemy dystrybuantę
22 przedstawienie rozkładu prawdopodobieństwa
Rozkład prawdopodobieństwa można przedstawić w postaci analitycznej:
-tabelarycznej,
-analitycznej,
-graficznej (możliwe wyniki z odp. im prawdopodobieństwami oraz dystrybuanta).
23 Podać def funkcji rozkładu prawdopodobieństwa , def dystrybuanty, zależność dystrybuanty miedzy funkcją rozkładu prawdopodobieństwa.
Def funkcji rozkładu prawdopodobieństwa-rozkładem zmiennej losowej dyskretnej nazywamy zestawienie jej możliwych wartości z odpowiadającymi im prawdopodobieństwami
Dystrybuanta empiryczna ![]()
Dystrybuanta zmiennej losowej określa prawdopodobieństwo tego, że zmienna losowa X przyjmie jakąkolwiek wartość mniejszą od z góry przyjętej danej wartości xi
Jak dodamy odpowiednie prawdopodobieństwa w przedziałach to otrzymamy dystrybuantę
24 Formy rozkładu prawdopodobieństwa+ przykłady ??????
Rozkład ciągły: Rozkład normalny, normalny standaryzowany, wykładniczy, studenta, trójkątny, chi-kwadrat
Rozkład dyskretny: Rozkład dwumianowy Bernuliego, Poisona, jednopunktowy, dwupunktowy, równomierny.
25 Dany jest rozkład N(0,1).Jakie jest prawdopodobieństwo że zmienna losowa przyjmie wartości nieujemne
Pole powierzchni pod całą krzywą równa się `1' więc pod połową `0.5'- Chyba
26 wyznaczyć prawdopodobieństwo przyjęcia przez zmienną losową o rozkładzie N(0,1), dowolnej wartości z przedziału(-3,3)
F(3)= 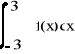
f(x)-krzywa pod którą liczymy pole
F(3)-dystrybuanta
27 Przedstawić graficznie funkcje rozkładu prawdopodobieństwa oraz odpowiadającą jej dytrybuantę
x 1 2 3 4
P 0.3 0.1 0.4 0.2
??????????????????
-co to jest standaryzacja zmiennej losowej
-przedstawić graficznie zależność P{|Ua|<U}=a gdzie V -zmienna losowa o rozkładzie N(0,1)
-narysować i opisać ogólna postać modelu obiektu badań w planowaniu eksperymentu. Objaśnic oznaczenia
-plan eksperymentu 3 poziomowy(3k ) narysować dla x1 i x2
-stan obiektu badań
-na czym polega tworzenie planów kompozycyjnych.
-definicja funkcji niezawodności i do czego ma zastosowanie
1
7
Wyszukiwarka
Podobne podstrony:
SMiPE - Kolokwium wykład ściąga 1, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperym
SMiPE - Kolokwium wykład ściąga 2, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperym
Statystyka3, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu, SMiPE
4 Rozklad normalny, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu, SMiPE
Statystyka matematyczna - ściąga 01, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksper
Statystyka matematyczna - ściąga 02, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksper
Opracowanie pytań na biurowe, Cosinus Technik Informatyk, semestr 1
Wymagania odnośnie projektu na zaliczenie wykładu ze Statystyki matematycznej
Boratyńska A Wykłady ze statystyki matematycznej
Statystyka2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
Statystyka5, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
opracowania sem4 SO BIGdzialajace pod WORDEM, Studia, Semestr IV, Systemy 2
statystyka1, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
zagadnienia na egzamin ze statystyki matematycznej zima 2014, Statystyka matematyczna
01 instrukcja mini, Studia, ZiIP, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu
Kucharski A Wykłady ze statystyki matematycznej
więcej podobnych podstron