Sortowanie Bąbelkowe
Bubble Sort
Jest to prosty algorytm sortujący o złożoności obliczeniowej O(n2). Pomimo swojej prostoty nie nadaje się do sortowania dużych zbiorów danych (za górną granicę przyjęto około 5000 elementów). Algorytm opiera się na kolejnych porównaniach dwóch sąsiednich elementów za pomocą funkcji porównującej. Jeśli porównywane elementy są w dobrej kolejności, to następuje przejście do następnego elementu. W przeciwnym razie elementy są zamieniane miejscami. Działanie to jest kontynuowane, aż wszystkie pary sąsiednich elementów w zbiorze będą ułożone we właściwej kolejności.
Przykład
Posortujemy metodą bąbelkową zbiór pięciu liczb: { 9 5 6 3 1 } w porządku rosnącym. Porządek rosnący oznacza, iż element poprzedzający jest zawsze mniejszy lub równy od elementu leżącego dalej w zbiorze. Nasza funkcja porównująca przyjmie zatem postać relacji mniejszy lub równy.
Algorytm sortowania bąbelkowego nie jest zbytnio efektywny dla nieuporządkowanych zbiorów danych. Jednak jeśli zbiór jest w większości uporządkowany (tylko kilka elementów znajduje się na niewłaściwym miejscu), to złożoność obliczeniowa zbliża się do klasy O(n), a więc czas sortowania zależy liniowo od liczby elementów, co powoduje, iż wciąż można go zastosować w niektórych przypadkach.
Schemat blokowy
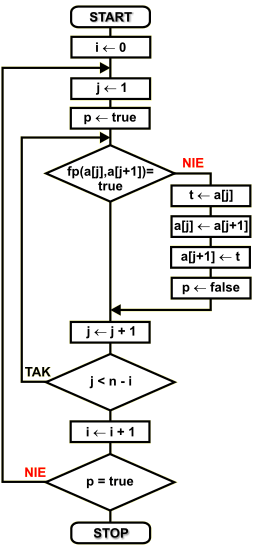
Dany jest zbiór { a1 a2 a3 ...an-2 an-1 an }, który należy posortować zgodnie z funkcją porównującą fp(...). W algorytmie zastosowano następujące zmienne:
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n, podanym w klamrach kwadratowych |
i , j |
zmienne używane na liczniki pętli |
p |
zmienna logiczna używana do sprawdzenia, czy cały zbiór jest już posortowany |
t |
zmienna tymczasowa używana przy wymianie zawartości elementów tablicy |
Algorytm rozpoczynamy nadając zmiennej i wartość 0. Zmienna ta pełni funkcję: licznika elementów, które zostały już uporządkowane na końcu zbioru - patrz przykład. Ponieważ jeszcze nie uporządkowano żadnych elementów, dlatego i przyjmuje wartość 0.
W pętli wewnętrznej porównujemy ze sobą kolejne elementy zbioru z elementem następnym. Zmienna p jest znacznikiem uporządkowania zbioru. Przed wejściem do pętli ustawiana jest na wartość logiczną true. Jeśli wewnątrz pętli elementy nie są uporządkowane, tzn. funkcja porównująca fp( a[j] , a[j+1] ) daje w wyniku wartość logiczną false, porównywane elementy są ze sobą zamieniane i znacznik p przyjmuje wartość false. Spowoduje to następny obieg pętli zewnętrznej, która wykonuje się do momentu, aż p będzie miało wartość logiczną true, czyli nie wystąpiła żadna zamiana elementów zbioru, co oznacza jego uporządkowanie.
Po porównaniu elementów i ewentualnej zamianie ich miejsc następuje zwiększenie indeksu j. Jeśli w zbiorze pozostały jeszcze jakieś elementy do porównania, to wykonywany jest następny obieg pętli wewnętrznej.
W przeciwnym razie pętla wewnętrzna jest kończona i następuje zwiększenie o 1 licznika pętli zewnętrznej. Powoduje to zmniejszenie o 1 liczby elementów do porównania w zbiorze - każdy obieg pętli zewnętrznej ustala pozycję ostatniego elementu zbioru - w następnym obiegu nie musimy go już sprawdzać, co przy dużej liczbie elementów znacznie zmniejsza ilość wykonywanych porównań.
Jeśli znacznik uporządkowania zbioru p ma wartość false, to następuje kolejny obieg pętli zewnętrznej. Jest to konieczne, ponieważ zbiór może być nieuporządkowany. Sortowanie kończymy dopiero wtedy, gdy wszystkie pary kolejnych elementów są we właściwym porządku i w trakcie przeglądania zbioru nie wystąpiło żadne przestawienie elementów. Zwróćmy uwagę, iż jeśli zbiór jest w dużej mierze uporządkowany, to algorytm zakończy się po kilku obiegach pętli zewnętrznej, a więc jest dosyć efektywnym rozwiązaniem.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
Przykład w C++
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,t,p,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ )
a[i] = b[i] = 1 + rand() % (n + n);
// sortowanie bąbelkowe
i = 0;
do
{
p = 1;
for(j = 0; j < n - i - 1; j++)
if(!fp(a[j],a[j+1]))
{
t = a[j];
a[j] = a[j + 1];
a[j + 1] = t;
p = 0;
};
i++;
}
while(p == 0);
// wyświetlamy wyniki
cout << "Sortowanie babelkowe" << endl
<< "(C)2003 mgr Jerzy Walaszek" << endl << endl
<< " lp przed po" << endl
<< "------------------------" << endl;
for(i = 0; i < n; i++)
{
cout.width(4); cout << i;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
Sortowanie przez Wstawianie
Insertion Sort
Algorytm sortowania przez wstawianie należy również do klasy złożoności obliczeniowej O(n2), lecz w porównaniu do opisanego wcześniej algorytmu sortowania bąbelkowego jest dużo szybszy i bardziej efektywny, lecz oczywiście bardziej złożony koncepcyjnie. Zasada działania tego algorytmu przypomina układanie w ręce kart pobieranych z talii. W skrócie możemy opisać go tak:
Na końcu (lub na początku) zbioru tworzymy uporządkowaną listę elementów. Najpierw lista ta składa się z ostatniego elementu. Ze zbioru wyciągamy przedostatni element. Miejsce, które zajmował staje się puste. Sprawdzamy, czy wyciągnięty element jest w dobrej kolejności z elementem ostatnim. Jeśli tak, to wstawiamy go z powrotem do zbioru. Jeśli nie, to na jego miejsce przesuwamy element ostatni, a na miejsce elementu ostatniego wstawiamy wyciągnięty element. W efekcie na końcu zbioru mamy już dwa elementy w dobrej kolejności. Teraz kolejno wybieramy elementy od końca zbioru i wstawiamy je w odpowiednie miejsce tworzonej na końcu listy. Elementy wcześniejsze są przesuwane na liście o jedną pozycję w lewo. Operacje te są kontynuowane aż do wstawienia pierwszego elementu. W efekcie otrzymujemy posortowany zbiór.
Wstawianie elementu do listy uporządkowanej
Prezentowany algorytm sortowania przez wstawianie wymaga wstawiania elementu zbioru do listy uporządkowanej. Mamy element wybrany ze zbioru. Naszym zadaniem jest przeszukanie listy uporządkowanej i znalezienie pozycji, na której ma się znaleźć wybrany element. Zadanie to wykonamy najprościej rozpoczynając przeglądanie od początku listy uporządkowanej. Jeśli funkcja 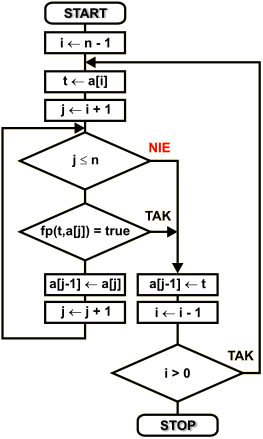
porównująca przyjmuje wartość false dla elementu wybranego i elementu z listy, to element z listy uporządkowanej przenosimy na poprzednią pozycję i przechodzimy do sprawdzenia kolejnego elementu na liście. Jeśli funkcja porównująca przyjmie wartość true, to element wybrany umieszczamy na poprzednim miejscu na liście uporządkowanej (poprzednie miejsce w stosunku do aktualnie testowanego jest zawsze wolne!).
W przykładzie przedstawionym poniżej wstawiamy liczbę 6 do lity {2 4 5 7 9}. Funkcja porównująca wyznacza porządek rosnący (ma wartość true, jeśli kolejne argumenty są w porządku rosnącym).
Schemat blokowy
Dany jest zbiór { a1 a2 a3 ...an-2 an-1 an }, który należy posortować zgodnie z funkcją porównującą fp(...). Do opisu algorytmu stosujemy następujące zmienne:
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n, podanym w klamrach kwadratowych |
i , j |
zmienne używane na liczniki pętli |
t |
zmienna tymczasowa używana do przechowania wstawianego elementu |
Pętla zewnętrzna wykona n-1 obiegów. Na początku zmienną licznikową tej pętli ustawiamy na wartość n-1. Wskazuje ona przedostatni element zbioru. Element ten wybieramy do wstawiania. Najpierw zapamiętujemy go w zmiennej tymczasowej t. Dzięki temu pozycja zajmowana przez ten element zostaje zwolniona.
W pętli wewnętrznej sterowanej zmienną j przeszukujemy tworzoną na końcu zbioru listę uporządkowaną w poszukiwaniu pozycji wstawienia wybranego wcześniej elementu. Wszystkie elementy mniejsze na liście uporządkowanej są przesuwane o jedną pozycję wstecz. Przeszukiwanie listy uporządkowanej kończy się w dwóch przypadkach:
1. Osiągnięto koniec listy - wybrany element jest większy wg funkcji porównującej od wszystkich elementów na liście uporządkowanej.
2. Funkcja porównująca przyjmuje wartość true, co oznacza, iż wybrany element powinien być umieszczony przed testowanym elementem listy uporządkowanej.
Gdy pętla wewnętrzna zakończy swoje działanie, to w obu możliwych przypadkach zmienna j zawiera pozycję o 1 większą od pozycji wstawiania. Dlatego element wybrany wpisujemy na pozycję a[j - 1].
Zmniejszamy licznik pętli zewnętrznej, sprawdzamy, czy nie osiągnął on wartości końcowej. Jeśli nie, to kontynuujemy z następnym elementem zbioru. W przeciwnym wypadku kończymy wykonywanie algorytmu sortowania.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,t,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ )
a[i] = b[i] = 1 + rand() % (n + n);
// sortowanie przez wstawianie
for(i = n - 2; i >= 0; i--)
{
t = a[i];
for(j = i + 1; (j < n) && !fp(t,a[j]); j++) a[j - 1] = a[j];
a[j - 1] = t;
};
// wyświetlamy wyniki
cout << "Sortowanie przez wstawianie\n"
<< "(C)2003 mgr Jerzy Walaszek\n\n"
<< " lp przed po\n"
<< "------------------------\n";
for(i = 0; i < n; i++)
{
cout.width(4); cout << i + 1;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
}
Sortowanie przez Selekcję
Selection Sort
Algorytm sortowania przez selekcję należy do algorytmów sortujących o klasie złożoności obliczeniowej O(n2). Nie jest on często stosowany, ponieważ opisany w poprzednim rozdziale algorytm sortowania przez wstawianie ma tą samą złożoność, a jest nieco szybszy. Zasada działania jest bardzo prosta. Najpierw szukamy w zbiorze elementu najmniejszego. Gdy zostanie znaleziony, wymieniamy go z pierwszym elementem zbioru. Następnie zbiór pomniejszamy o ten pierwszy element, który ustawiony został już na właściwej pozycji. W tak pomniejszonym zbiorze znów szukamy elementu najmniejszego i wstawiamy go na drugą pozycję. Zbiór pomniejszamy i kontynuujemy te same operacje wyszukiwań i wstawień, aż wszystkie elementy zbioru zostaną posortowane.
Przykład
Posortujemy tą metodą zbiór pięciu liczb: { 9 5 6 3 1 } w porządku rosnącym. Nasza funkcja porównująca przyjmie więc postać relacji mniejszy lub równy.
{ 9 5 6 3 1 } |
W zbiorze szukamy najmniejszego elementu. Jest nim liczba 1. |
{ 1 5 6 3 9 } |
Ponieważ najmniejszy element nie jest na pierwszej pozycji, więc wymieniamy go z elementem pierwszym, czyli 9. |
1 { 5 6 3 9 } |
W pomniejszonym zbiorze szukamy elementu najmniejszego. Jest nim liczba 3. |
1 { 3 6 5 9 } |
Znaleziony element najmniejszy wymieniamy z pierwszym elementem. |
1 3 { 6 5 9 } |
Na właściwym miejscu są już dwa elementy zbioru. Wśród pozostałych elementów znajdujemy element najmniejszy. |
1 3 { 5 6 9 } |
Wymieniamy go z pierwszym elementem zbioru |
1 3 5 { 6 9 } |
Na właściwym miejscu są już trzy elementy. Ponieważ pozostały zbiór posiada więcej niż jeden element, dalej szukamy elementu najmniejszego. Ponieważ element najmniejszy jest już na pierwszym miejscu, nie wykonujemy żadnych przestawień. |
{ 1 3 5 6 9 } |
Po wykonaniu ostatniej operacji wszystkie elementy zostały posortowane. |
Wyszukanie najmniejszego elementu w zbiorze
W podanym algorytmie występuje problem znalezienia najmniejszego elementu w zbiorze względem zadanej funkcji porównującej. Element najmniejszy zdefiniujmy następująco:
a D jest najmniejszy, jeśli dla każdego b D i a ≠ b zachodzi fp(a,b) = true.
Z definicji tej można wywnioskować, iż najmniejszy element nie jest poprzedzony żadnym innym elementem zbioru, który się od niego różni. Jest to dosyć istotne spostrzeżenie, ponieważ zbiory mogą posiadać elementy o identycznej zawartości. Funkcja porównująca nie określa kolejności względem siebie elementów identycznych, tzn. ponieważ elementy te są sobie równe, więc ich kolejność jest zwykle nieistotna.
Element najmniejszy znajdujemy następująco: za tymczasowy element najmniejszy przyjmujemy pierwszy element zbioru. Następnie porównujemy go kolejno ze wszystkimi pozostałymi elementami za pomocą funkcji porównującejj. Jeśli dla jakiegoś elementu funkcja ta przyjmie wartość logiczną false, to element ten będzie mniejszy od tymczasowego i zastąpimy nim najmniejszy element tymczasowy.
Oto odpowiedni przykład: naszym zadaniem jest wyszukanie najmniejszego elementu w zbiorze { 4 7 3 2 5 1 }. Niech funkcja porównująca ustala porządek rosnący.
{ 4 7 3 2 5 1 } |
Za tymczasowy najmniejszy element przyjmujemy pierwszy element zbioru, czyli 4. |
{ 4 7 3 2 5 1 } |
Następnie porównujemy go kolejno z pozostałymi elementami zbioru: |
{ 4 7 3 2 5 1 } |
fp(4,3) = false - znaleźliśmy element mniejszy, więc za nowy element najmniejszy przyjmujemy wartość 3 |
{ 4 7 3 2 5 1 } |
Kontynuujemy przeglądanie ze znalezionym najmniejszym elementem tymczasowym: |
{ 4 7 3 2 5 1 } |
fp(2,5) = true - dobra kolejność, liczba 2 pozostaje elementem najmniejszym |
{ 4 7 3 2 5 1 } |
fp(2,1) = false - zła kolejność, znaleźliśmy nowy element najmniejszy - 1 |
{ 4 7 3 2 5 1 } |
Ponieważ przeglądnęliśmy wszystkie elementy zbioru, to wartość 1 jest najmniejsza wg funkcji porównującej ten zbiór. |
Schemat blokowy
Dany jest zbiór { a1 a2 a3 ...an-2 an-1 an }, który należy posortować zgodnie z funkcją porównującej 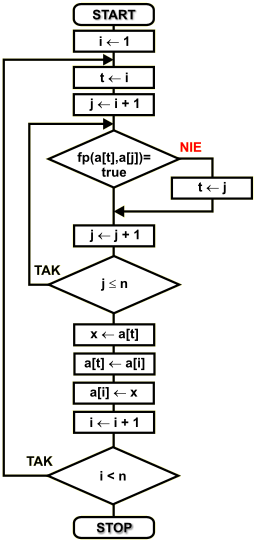
fp(...). Do opisu algorytmu stosujemy następujące zmienne:
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n podanym w klamrach kwadratowych |
i , j |
zmienne używane na liczniki pętli |
t |
zmienna przechowująca indeks elementu najmniejszego |
x |
zmienna pomocnicza |
Zmienna i otrzymuje na początku wartość 1. Pełni ona rolę licznika obiegów pętli zewnętrznej oraz elementów posortowanych - znajdujących się na właściwej pozycji.
Zmienna t zawiera indeks najmniejszego elementu. Na początku pętli wewnętrznej przyjmuje ona numer pierwszego elementu w zbiorze, czyli i-ty. Następnie przeszukujemy pozostałą część zbioru w poszukiwaniu elementów mniejszych. Jeśli takie zostaną znalezione, to ich indeksy będą wprowadzone do zmiennej t. Kryterium znajdowania elementu najmniejszego ustala funkcja porównująca dla tego zbioru.
Po przeszukaniu całego zbioru w t mamy indeks najmniejszego elementu. Wymieniamy pierwszy element zbioru (i-ty) z elementem najmniejszym. Dzięki tej operacji na początek zbioru trafia element najmniejszy, który znajduje się już na właściwej pozycji.
Zmienna i zostaje zwiększona o 1, co powoduje zmniejszenie zbioru do posortowania i przejście do kolejnego elementu. Pętla jest kontynuowana, aż wszystkie elementy zbioru zostaną posortowane.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,t,x,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ )
a[i] = b[i] = 1 + rand() % (n + n);
// sortowanie przez wybór
for(i = 0; i < n - 1; i++)
{
t = i;
for(j = i + 1; j < n; j ++)
if(!fp(a[t],a[j])) t = j;
x = a[t]; a[t] = a[i]; a[i] = x;
};
// wyświetlamy wyniki
cout << "Sortowanie przez wybor" << endl
<< "(C)2003 mgr Jerzy Walaszek" << endl << endl
<< " lp przed po" << endl
<< "------------------------" << endl;
for(i = 0; i < n; i++)
{
cout.width(4); cout << i + 1;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
}
Sortowanie Metodą Shella
Shell Sort
Algorytm ten został zaproponowany przez Donalda Shella w 1959 roku. Jest to najszybszy algorytm sortujący w klasie O(n2). Idea jest następująca: Shell zauważył, iż algorytm sortowania przez wstawianie (insertion sort) jest bardzo efektywny, gdy zbiór jest już w dużej części uporządkowany. Wtedy złożoność obliczeniowa jest prawie liniowa - O(n). Jednakże algorytm ten nieefektywnie przestawia elementy w trakcie sortowania - ponieważ porównywane są kolejne elementy na liście uporządkowanej, to ulegają one przesunięciu tylko o jedną pozycję przy każdym obiegu pętli wewnętrznej. Shell wpadł na pomysł modyfikacji algorytmu sortowania przez wstawianie tak, aby porównywane były na początku elementy odległe od siebie, a później ta odległość malała i w końcowej fazie powstawałby zwykły algorytm sortowania przez wstawianie, lecz ze zbiorem jest już w dużym stopniu uporządkowanym.
Osiągnął to dzieląc w każdym obiegu zbiór na odpowiednią liczbę podzbiorów, których elementy są od siebie odległe o stałą odległość g. Następnie każdy z podzbiorów jest sortowany za pomocą sortowania przez wstawianie. Powoduje to częściowe uporządkowanie zbioru. Dalej odległość g jest zmniejszana (najczęściej o połowę), znów są tworzone podzbiory (jest ich teraz mniej) i następuje kolejna faza sortowania. Operacje te kontynuujemy aż do momentu, gdy odległość g osiągnie wartość 0. Wtedy zbiór wyjściowy będzie uporządkowany.
Zasadniczym czynnikiem wpływającym na efektywność algorytmu sortowania metodą Shella jest odpowiedni dobór ciągu kolejnych odstępów. Shell zaproponował przyjęcie na początku odstępu równego połowie liczby elementów w zbiorze, a następnie zmniejszanie tego odstępu o połowę przy każdym obiegu pętli. Nie jest to najbardziej efektywne rozwiązanie, jednak najprostsze w implementacji. Dlatego będziemy z niego korzystać.
Przykład
Posortujemy metodą Shella zbiór ośmiu liczb: { 4 2 9 5 6 3 8 1 } w porządku rosnącym. Nasza funkcja porównująca przyjmie więc postać relacji mniejszy lub równy. Zbiór posiada osiem elementów, zatem przyjmiemy na wstępie odstęp g równy 4. Taki odstęp podzieli zbiór na 4 podzbiory, których elementy będą elementami zbioru wejściowego odległymi od siebie o 4 pozycje:
{ 4 2 9 5 6 3 8 1 } - zbiór podstawowy
{ 5 1 } - pierwszy podzbiór, elementy a4 i a8
{ 9 8 } - drugi podzbiór, elementy a3 i a7
{ 2 3 } - trzeci podzbiór, elementy a2 i a6
{ 4 6 } - czwarty podzbiór, elementy a1 i a5
Teraz każdy z otrzymanych podzbiorów sortujemy algorytmem sortowania przez wstawianie. Ponieważ zbiory te są dwuelementowe, to sortowanie pędzie polegało na porównaniu pierwszego elementu podzbioru z elementem drugim i ewentualną zamianę ich miejsc, jeśli będą w niewłaściwym porządku określonym funkcją porównującą.
{ 5 1 } |
Podzbiór pierwszy. Niewłaściwa kolejność, zamieniamy miejscami |
{ 9 8 } |
Podzbiór drugi. Niewłaściwa kolejność, zamieniamy miejscami |
{ 2 3 } |
Podzbiór trzeci. Kolejność dobra, pozostawiamy bez zmian. |
{ 4 6 } |
Podzbiór czwarty. Kolejność dobra, pozostawiamy bez zmian |
Po pierwszym obiegu otrzymujemy następujący wynik uporządkowania zbioru:
{ 1 5 } - pierwszy podzbiór, elementy a4 i a8
{ 8 9 } - drugi podzbiór, elementy a3 i a7
{ 2 3 } - trzeci podzbiór, elementy a2 i a6
{ 4 6 } - czwarty podzbiór, elementy a1 i a5
{ 4 2 8 1 6 3 9 5 } - zbiór podstawowy
Zmniejszamy odstęp g o połowę, więc g = 2. Zbiór podstawowy zostanie podzielony na dwa podzbiory:
{ 4 2 9 5 6 3 8 1 } - zbiór podstawowy
{ 2 5 3 1 } - pierwszy podzbiór, elementy a2, a4, a6 i a8
{ 4 9 6 8 } - drugi podzbiór, elementy a1, a3, a5 i a7
Każdy z tych podzbiorów sortujemy przez wstawianie:
{ 2 5 3 1 } |
Na końcu tworzymy listę uporządkowaną, a kolejne elementy wstawiamy na tą listę począwszy od przedostatniego i skończywszy na pierwszym. |
3 |
1 przesuwamy na puste miejsce, a 3 umieszczamy na zwolnionej pozycji. Lista uporządkowana zawiera już 2 elementy. |
5 |
1 i 3 przesuwamy o jedną pozycję w lewo, a 5 umieszczamy na zwolnionej pozycji. Lista uporządkowana ma już 3 elementy |
2 |
1 przesuwamy na wolne miejsce, a 2 wstawiamy na zwolnioną pozycję pomiędzy 1 a 3. Podzbiór pierwszy został uporządkowany |
{ 4 9 6 8 } |
W taki sam sposób porządkujemy podzbiór drugi |
6 |
Ponieważ 6 jest w dobrym porządku z 8, to nie dokonujemy wymiany elementów. |
9 |
6 i 8 przesuwamy o jedną pozycję w lewo, a 9 wstawiamy na koniec listy uporządkowanej. |
4 |
4 jest w dobrej kolejności, więc nie dokonujemy wstawiania wewnątrz listy. |
Po drugim obiegu otrzymujemy następujący wynik uporządkowania zbioru wejściowego:
{ 1 2 3 5 } - pierwszy podzbiór, elementy a2, a4, a6 i a8
{ 4 6 8 9 } - drugi podzbiór, elementy a1, a3, a5 i a7
{ 4 1 6 2 8 3 9 5 } - zbiór podstawowy
Zmniejszamy odstęp g o połowę, g = 1. Taki odstęp nie dzieli zbioru wejściowego na podzbiory, więc teraz będzie sortowany przez wstawianie cały zbiór. Jednak algorytm sortujący ma ułatwioną pracę, ponieważ dzięki poprzednim dwóm obiegom zbiór został częściowo uporządkowany - elementy małe zbliżyły się do początku zbioru, a elementy duże do końca.
{ 4 1 6 2 8 3 9 5 } |
Na końcu tworzymy listę uporządkowaną, a kolejne elementy wstawiamy na tą listę począwszy od przedostatniego i skończywszy na pierwszym. |
9 |
5 przesuwamy na wolną pozycję, a 9 wstawiamy na koniec listy. |
3 |
3 pozostawiamy na miejscu |
8 |
3 i 5 przesuwamy o 1 pozycję w lewo, a 8 wstawiamy na zwolnione miejsce pomiędzy 5 i 9 |
2 |
2 pozostawiamy na miejscu. |
6 |
2, 3 i 5 przesuwamy o 1 pozycję w lewo. Na zwolnione miejsce wstawiamy 6. |
1 |
1 pozostawiamy na swoim miejscu. |
4 |
1, 2 i 3 przesuwamy o 1 pozycję w lewo. Na zwolnione miejsce pomiędzy 3 a 5 wstawiamy 4. Zbiór jest uporządkowany. |
Zaleta algorytmu sortującego metodą Shella ujawni się przy dużej liczbie elementów. W takim przypadku zbiór zostaje najszybciej posortowany ze wszystkich algorytmów sortujących klasy O(n2). Algorytm można jeszcze bardziej zoptymalizować dobierając odpowiednio ciąg odstępów g, lecz tym zagadnieniem nie będziemy się tutaj zajmować.
Schemat blokowy
Dany jest zbiór { a1 a2 a3 ...an-2 an-1 an }, który należy posortować zgodnie z funkcją porównującą fp(...). Do opisu algorytmu stosujemy następujące zmienne:
n |
liczba elementów w zbiorze |
||
a[...] |
element zbioru o numerze od 1 do n, podanym w klamrach kwadratowych |
||
i , j |
zmienne używane na liczniki pętli |
||
g |
zmienna przechowująca odstęp pomiędzy sortowanymi elementami. |
||
t |
zmienna tymczasowa używana przy wymianie zawartości elementów tablicy |
||
Algorytm sortujący Shella |
Algorytm sortowania przez wstawianie |
||
W celach porównawczych rozmyślnie umieściliśmy powyżej schematy blokowe algorytmu sortowania metodą Shella oraz przez wstawianie. Zwróćcie uwagę na ich podobieństwo. Algorytm Shella jest modyfikacją algorytmu sortowania przez wstawianie polegającą na tym, iż nie jest sortowany od razu cały zbiór, lecz jego podzbiory. Do tego celu służy właśnie odstęp g, który w algorytmie Shella jest zmienny, a w sortowaniu przez wstawianie jest stały i wynosi 1. Dodatkowa oprawa algorytmu Shella zawiera więc obsługę zmian odstępu g. Pozostała część jest praktycznie taka sama jak w algorytmie sortowania przez wstawianie.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,t,g,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ )
a[i] = b[i] = 1 + rand() % (n + n);
// sortowanie metodą Shella
for(g = n / 2; g > 0; g /= 2)
for(i = n - g - 1; i >= 0; i--)
{
t = a[i];
for(j = i + g; (j < n) && !fp(t,a[j]); j += g)
a[j - g] = a[j];
a[j - g] = t;
};
// wyświetlamy wyniki
cout << "Sortowanie metoda Shella" << endl
<< "(C)2003 mgr Jerzy Walaszek" << endl << endl
<< " lp przed po" << endl
<< "------------------------" << endl;
for(i = 0; i < n; i++)
{
cout.width(4); cout << i + 1;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
}
Sortowanie przez Kopcowanie
Heap Sort
Wszystkie opisane poprzednio algorytmy mają jedną podstawową wadę - należą do klasy złożoności obliczeniowej O(n2), co oznacza, iż w najgorszym przypadku czas sortowania rośnie z kwadratem liczby sortowanych elementów. Przy dużej ich liczbie (sięgającej dziesiątków lub setek tysięcy) sortowanie może zająć nawet najszybszemu komputerowi dużą ilość czasu (nawet wiele wieków!).
Zachodzi więc naturalne pytanie, czy nie da się tego zrobić szybciej? Odpowiedź jest pozytywna. Wymyślono wiele algorytmów sortujących, które należą do klasy złożoności obliczeniowej O(n log2n) - liniowo logarytmicznej. Ponieważ logarytm z n jest zawsze mniejszy od n (dla n >= 1), to ich iloczyn jest mniejszy od n2, co zapisujemy:
n log2 n < n2
Wobec tego algorytm o złożoności obliczeniowej klasy O(n log2n) wykona się o wiele szybciej od algorytmu klasy O(n2). Różnica ta jest szczególnie drastyczna dla dużych wartości n. Dzięki temu algorytmy sortujące klasy O(n log2n) nadają się szczególnie do sortowania dużych ilości elementów, gdzie wyraźnie korzystamy z ich zalet. Wadą tych algorytmów jest większa złożoność w stosunku do opisanych metod sortowania zbiorów danych. Z drugiej strony nic nie przychodzi darmo.
Pierwszy z szybkich algorytmów sortujących wykorzystuje specjalną strukturę danych, zwaną kopcem (ang. Heap). Przed opisem samego algorytmu zajmiemy się własnościami kopca oraz sposobami jego tworzenia i pobierania z niego danych.
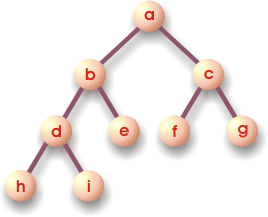
Drzewo binarne
Drzewo binarne (ang. binary tree - Btree) jest hierarchiczną strukturą danych, w której elementy noszą nazwę węzłów. Każdy węzeł może się łączyć z dwoma kolejnymi węzłami. Na przykład węzeł b łączy się z węzłami d i e. Węzły d i e noszą nazwę węzłów potomnych węzła b lub potomków węzła b. Węzeł b jest dla węzłów d i e węzłem rodzicielskim lub przodkiem. Węzły posiadające potomków nazywamy gałęziami - np. a, b, c, d. Węzły nie posiadające potomków noszą nazwę liści - e, f, g, h, i. Pierwszy węzeł, z którego wyrasta całe drzewo nazywa się węzłem głównym lub korzeniem - jest to węzeł a.
Nazwa drzewa pochodzi od własności posiadania przez każdy węzeł do dwóch potomków. W języku angielskim słówko binary oznacza dwójkowy - 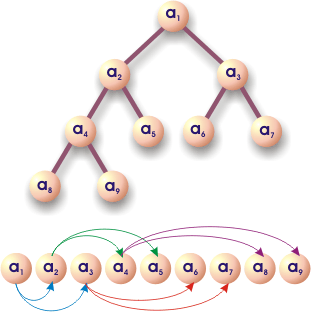
binary tree - drzewo dwójkowe.
Drzewa binarne da się w prosty sposób odwzorować w pamięci komputera, jeśli tworzące je elementy będą umieszczone w tej pamięci obok siebie - tak dzieje się w tablicach. Rozważmy poniższe drzewo binarne:
Węzeł tworzony przez element a1 posiada dwóch potomków - a2 oraz a3. Węzeł a2 posiada również dwóch potomków - a4 i a5. Jeśli dokładnie przyjrzymy się indeksom elementów tworzących drzewo binarne, to musimy dojść do następującego wniosku:
Jeśli węzeł utworzony przez element ai ma potomków, to muszą to być elementy a2 x i oraz a2 x i + 1. Innymi słowy indeksy potomków węzła i-tego mają wartość:
2 x i - lewy potomek węzła i-tego
2 x i + 1 - prawy potomek węzła i-tego.
Teraz rozważmy przodków danego węzła. Tutaj również przyjrzenie się indeksom da nam szybką odpowiedź - przodkiem węzła i-tego (i musi być większe od 1, ponieważ korzeń drzewa nie posiada przodka) jest węzeł o indeksie równym |i / 2| (część całkowita z dzielenia).
Wzory te pozwalają odwzorować liniowy ciąg elementów (tablicę) w drzewo binarne i na odwrót. Na rysunku poniżej drzewa binarnego widzimy powiązania poszczególnych elementów w takiej strukturze.
Przykład
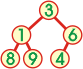
Przedstawić w postaci drzewa binarnego następujący ciąg elementów { 3 1 6 8 9 4 }
|
Tworzenie drzewa rozpoczynamy od korzenia, którym jest pierwszy element ciągu, czyli 3. |
|
Do korzenia dołączamy węzły potomne, są to kolejne dwa elementy - 1 i 6 |
|
Przechodzimy na następny poziom struktury drzewa i do lewego węzła [1] dołączamy jego węzły potomne - kolejne dwa elementy ze zbioru, czyli 8 i 9. |
|
Pozostał nam ostatni element, który jest potomkiem węzła [6]. |
Kopiec
Kopiec jest drzewem binarnym, w którym istnieją zależności pomiędzy węzłami potomnymi a ich przodkiem wyznaczone przez funkcję porównującą w sposób następujący:
Dla każdego węzła posiadającego potomków zachodzi
fp(potomek,przodek) = true
Innymi słowy, jeśli funkcja porównująca wyznacza porządek rosnący, to w strukturze kopca każdy przodek ma wartość większą lub równą wartości swoich potomków. Korzeń kopca ma największą wartość - jest elementem maksymalnym.
|
|
Zwróć uwagę, iż uporządkowanie elementów w kopcu nie gwarantuje uporządkowania w odwzorowującym go zbiorze. Przykładowo podany kopiec ma w tablicy reprezentację { 9 8 6 1 3 4 } i nie jest uporządkowany.
Tworzenie kopca
Kopiec tworzymy podobnie jak zwykłe drzewo binarne - dołączamy elementy na końcu struktury. Jednak tutaj musimy sprawdzać, czy po dołączeniu kolejnego liścia zostaje zachowana struktura kopca. Jeśli po dołączeniu elementu jest on większy od swojego przodka, to musimy elementy te zamienić miejscami. Następnie przenosimy się na wyższy poziom struktury drzewa i sprawdzamy, czy wymieniony przodek jest mniejszy od swojego przodka. Jeśli nie, to znów wymieniamy elementy i przechodzimy na poziom wyższy. Działanie te kontynuujemy, aż do momentu spełnienia warunku kopca (przodek większy od potomka ze względu na funkcję porównującą) lub po osiągnięciu korzenia kopca. Poniżej prezentujemy odpowiedni przykład.
Przykład
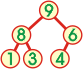
Utworzymy kopiec z następującego zbioru elementów: { 3 2 7 4 9 5 }. W kopcu określimy porządek rosnący - przodek ma wartość większą lub równą wartości każdego ze swoich potomków.
|
Korzeniem kopca będzie pierwszy element zbioru - liczba 3. |
|
Do korzenia dołączamy następny element - liczbę 2. Ponieważ potomek jest mniejszy od swojego przodka, więc warunek kopca został zachowany po dołączeniu i nie musimy wymieniać elementów. |
|
Pobieramy kolejny element ze zbioru - liczbę 7 i dołączamy go na końcu kopca. Po dołączeniu warunek kopca nie jest spełniony - potomek większy od przodka. Musimy dokonać wymiany elementów 3 i 7. |
|
Po wymianie otrzymujemy drzewo trójelementowe. w którym spełniony jest warunek kopca. |
|
Dołączamy kolejny element - liczbę 4. Warunek kopca nie jest spełniony, więc wymieniamy go z jego przodkiem. |
|
4 i 7 spełnia warunek kopca. |
|
Dołączamy na spodzie kopca kolejny element zbioru - liczbę 9. Warunek kopca nie jest spełniony, musimy dokonać wymiany potomka z przodkiem, czyli liczb 4 i 9. |
|
Po wymianie przesuwamy się na wyższy poziom i sprawdzamy warunek kopca. Nie jest spełniony, wymieniamy potomka z przodkiem, czyli liczby 9 i 7. |
|
Po tej zamianie warunek kopca jest spełniony we wszystkich węzłach. |
|
Dołączamy na spodzie kopca następny element ze zbioru - liczbę 5. Warunek kopca nie jest spełniony, wymieniamy potomka z przodkiem. |
|
Po wymianie warunek kopca jest spełniony dla każdego węzła. Ponieważ wyczerpaliśmy wszystkie elementy zbioru wejściowego, kopiec jest gotowy. Jeśli odwzorujemy go w ciąg elementów, otrzymamy zbiór { 9 7 5 2 4 3 }. |
Tworzenie kopca jest operacją o złożoności obliczeniowej klasy O(n). Oznacza to, iż np. dziesięciokrotny wzrost liczby elementów powoduje dziesięciokrotny wzrost czasu budowania kopca. Zwróćcie uwagę, iż przy wstawianiu nowych elementów wykonujemy niewiele operacji porównań i przestawień - maksymalnie tyle, ile wynosi liczba poziomów drzewa binarnego, która wyraża się prostym wzorem:
liczba poziomów = [log2(n)], n - liczba elementów-węzłów kopca.
Schemat blokowy tworzenia kopca
Kopiec zostanie utworzony poprzez odpowiednie przegrupowanie elementów zbioru. Taki sposób działania nazywamy tworzeniem kopca na miejscu - operacja ta nie wymaga dodatkowych zasobów komputera, wykorzystujemy obszar zajęty przez elementy zbioru.
Naszym zadaniem jest utworzenie kopca ze zbioru elementów { a1, a2, ..., an-1, an }, które nie są posortowane w żadnym porządku. Kolejność elementów w węzłach kopca definiujemy za pomocą funkcji porządkowej. Problem można rozwiązać na dwa sposoby - rekurencyjnie lub iteracyjnie. Ja wybrałem rozwiązanie iteracyjne - czytelnik niech zastanowi się nad sposobem rekurencyjnym.
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n, podanym w klamrach kwadratowych |
i , j |
zmienne używane na liczniki pętli |
t |
zmienna tymczasowa używana przy wymianie zawartości elementów tablicy |
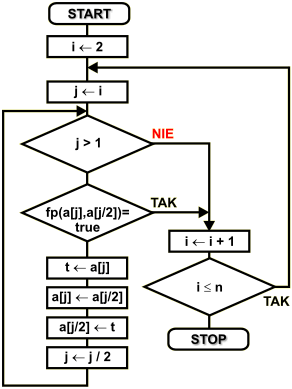
Tworzenie kopca rozpoczynamy od elementu drugiego. Pierwszy element zbioru automatycznie jest korzeniem kopca i nie musimy go nigdzie przemieszczać. Zmienna i wskazuje kolejne elementy umieszczane w kopcu. Zmienna j przechowuje indeksy kolejno sprawdzanych węzłów.
Po wstawieniu elementu do kopca na pozycji j-tej, sprawdzamy, czy węzeł ten ma przodka. Sytuacja taka wystąpi dla wszystkich węzłów o indeksie większym od 1. Indeks 1 wskazuje korzeń, który nie posiada przodka i w takim przypadku wychodzimy z pętli.
Jeśli węzeł posiada przodka, to sprawdzamy, czy zachodzi pomiędzy potomkiem a przodkiem warunek kopca: fp(potomek,przodek)=true. Jeśli tak, to wychodzimy z pętli i wstawiamy kolejny element aż do wyczerpania zbioru. Jeśli warunek kopca nie jest spełniony, to musimy wymienić ze sobą potomka i przodka, a następnie przejść na wyższy poziom struktury do węzła przodka i dokonać znów sprawdzenia warunku kopca. Operacje te wykonuje pętla lewa. Pętla prawa wstawia do kopca kolejne elementy.
Rozbiór kopca
W poprzednim rozdziale pokazaliśmy sposób tworzenia kopca ze zbioru ponumerowanych elementów. Teraz zajmiemy się drugą bardzo ważną operacją - rozbiorem kopca. Rozbiór kopca rozpoczynamy od jego korzenia, który zastępujemy ostatnim elementem w kopcu. Operacja ta powoduje zaburzenie struktury kopca, którą musimy odtworzyć. Dokonujemy tego porównując nowo utworzony węzeł z największym potomkiem. Jeśli warunek kopca nie jest zachowana, to dokonujemy zamiany przodka z potomkiem. Następnie przechodzimy na miejsce zamienionego potomka i kontynuujemy porównywanie, aż dojdziemy do spodu kopca lub stwierdzimy zachowanie warunku kopca. Poniżej przedstawiamy odpowiedni przykład:
Przykład
Naszym zadaniem jest rozebranie kopca przez kolejne pobieranie korzenia. Po pobraniu struktura kopca musi być przywrócona. Oto nasz kopiec do rozbioru:
|
9 |
Usuwamy z kopca korzeń - liczbę 9. Na to miejsce wstawiamy ostatni element - liczbę 3. Technicznie operacją taką realizujemy wymieniając miejscami korzeń z ostatnim liściem kopca i zmniejszając o 1 jego długość. |
|
|
Po wstawieniu do korzenia ostatniego liścia struktura kopca jest zaburzona - korzeń nie jest już największym elementem. Musimy więc odtworzyć kopiec. Korzeń porównujemy z jego potomkami - liczby 7 i 5. Dokonujemy wymiany z największym węzłem potomnym, czyli liczbą 7. |
|
|
Po dokonaniu wymiany przenosimy się do zmienionego węzła i dalej sprawdzamy warunek kopca - nie zachodzi, więc wymieniamy przodka (liczba 3) z największym potomkiem (liczba 4). |
|
|
Po tej operacji kopiec został zrekonstruowany i wszystkie węzły spełniają jego warunek. |
|
7 9 |
Usuwamy korzeń zastępując go najmłodszym liściem. |
|
|
Warunek kopca nie jest spełniony - wymieniamy korzeń z największym potomkiem. Ponieważ wymieniony węzeł nie ma już potomków, operacja odtwarzania warunków kopca została zakończona. |
|
5 7 9 |
Usuwamy korzeń i zastępujemy go ostatnim liściem kopca. |
|
|
Warunek kopca nie jest spełniony - wymieniamy przodka z największym potomkiem. |
|
4 5 7 9 |
Usuwamy korzeń, zastępujemy go ostatnim liściem. |
|
3 4 5 7 9 |
Usuwamy korzeń, zastępujemy go ostatnim liściem. |
|
2 3 4 5 7 9 |
Usuwamy ostatni węzeł kopca - rozbiór zakończony. |
Zwróć uwagę na usuwane z kopca elementy. Jeśli ustawimy je w odwrotnej kolejności, to utworzą ciąg posortowany zgodnie z kryterium funkcji porównującej.
Schemat blokowy rozbioru kopca
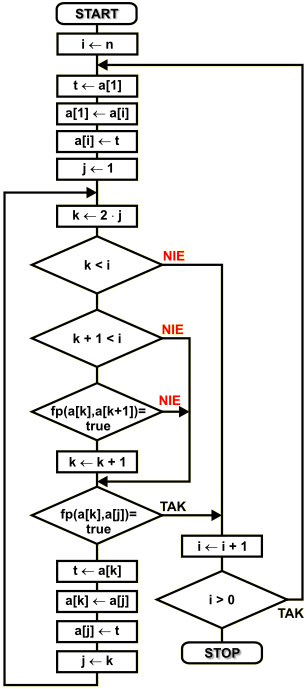
Zakładamy, iż kopiec jest utworzony w zbiorze ponumerowanych elementów { a1, ... ,an }. W wyniku działania algorytmu usuwane z kopca elementy będą wstawiane na kolejne od końca pozycje w zbiorze. Pozycje te są zajmowane przez najmłodszy liść kopca, który przenosimy do korzenia, więc zajmowane miejsce ulega zwolnieniu. Po wykonaniu wszystkich operacji rozbioru elementy zbioru będą posortowane rosnąco zgodnie z kryterium funkcji porównującej.
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n, podanym w klamrach kwadratowych |
i , j, k |
zmienne używane na liczniki pętli |
t |
zmienna tymczasowa używana przy wymianie zawartości elementów tablicy |
Zmienna i będzie wskazywać miejsce w zbiorze, do którego wstawiamy pobrany z kopca element. Dodatkowa funkcja tej zmiennej to określanie długości kopca, która jest zawsze o 1 mniejsza od aktualnej zawartości zmiennej i.
Rozpoczynamy od ostatniego miejsca w zbiorze. Element z tej pozycji zostaje wymieniony z korzeniem kopca. Ponieważ korzeń kopca zawiera największy element, to na końcu zbioru będzie tworzony ciąg posortowanych elementów.
Po wymianie sprawdzamy warunek kopca. Najpierw znajdujemy największego potomka - wskazuje go zmienna k. Jeśli potomek istnieje i jest większy od przodka, to zamieniamy ze sobą te węzły i przechodzimy do sprawdzania warunku kopca dla wymienionego potomka i jego węzłów potomnych. Jeśli węzeł nie posiada potomków lub jest dla nich spełniony warunek kopca, to wychodzimy z pętli wewnętrznej i przechodzimy do pobrania z kopca kolejnego elementu.
Operacje te są kontynuowane aż cały kopiec zostanie rozebrany. Wtedy zbiór będzie posortowany rosnąco zgodnie z kryterium funkcji porównującej.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
Sortowanie z wykorzystaniem kopca
Jeśli prześledziliście dokładnie opisane powyżej rozdziały, to powinniście już bez trudu podać zasadę sortowania z wykorzystaniem struktury kopca. Algorytm jest wręcz banalny i opiszemy go słownie tak:
Utwórz kopiec z elementów zbioru, który chcesz posortować.
Rozbierz kopiec wstawiając elementy do sortowanego zbioru
Zbiór jest posortowany.
Algorytm sortowania poprzez kopcowanie (ang. Heap Sort) należy do klasy złożoności obliczeniowej O(n log2n), co oznacza, iż nadaje się on do porządkowania dużych zbiorów danych. Sortowanie jest wykonywane nieporównywalnie szybciej w stosunku do opisanych poprzednio algorytmów sortujących klasy O(n2). Drugą jego zaletą jest to, iż jak widzieliśmy, nie wymaga on stosowania dodatkowych struktur danych - kopiec tworzony jest w miejscu zajmowanym przez sortowany zbiór - jest to bardzo istotna zaleta ze względu na zajętość pamięci operacyjnej komputera.
Przykład w C++
Wszystkie prezentowane tutaj przykłady zostały uruchomione w DevC++, który można darmowo i legalnie pobrać poprzez sieć Internet.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,k,t,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ )
a[i] = b[i] = 1 + rand() % (n + n);
// tworzymy kopiec z elementów tablicy a[]
for(i = 1; i < n; i++)
for(j = i; (j > 0) && !fp(a[j],a[(j-1)/2]); j = (j-1)/2)
{
t = a[j]; a[j] = a[(j-1)/2]; a[(j-1)/2] = t;
};
// rozbieramy kopiec
for(i = n - 1; i >= 0; i--)
{
t = a[0]; a[0] = a[i]; a[i] = t;
j = 0;
while(j != i)
{
k = j + j + 1;
if(k < i)
{
if((k+1 < i) && fp(a[k],a[k+1])) k++;
if(fp(a[k],a[j]))
j = i;
else
{
t = a[k]; a[k] = a[j]; a[j] = t;
j = k;
};
}
else j = i;
};
};
// wyświetlamy wyniki
cout << "Sortowanie przez kopcowanie" << endl
<< "(C)2003 mgr Jerzy Walaszek" << endl << endl
<< " lp przed po" << endl
<< "------------------------" << endl;
for(i = 0; i < n; i++)
{
cout.width(4); cout << i + 1;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
}
Sortowanie Szybkie
Quick Sort
Sortowanie szybkie jest najszybszym z algorytmów sortujących należących do klasy złożoności obliczeniowej O( n log2n), chociaż w pewnych niekorzystnych przypadkach, algorytm ten może stać się niestabilny. Zasada jego działania jest bardzo prosta, lecz trudna w implementacji. Ze zbioru wejściowego wybieramy jeden element, który dalej będziemy nazywać elementem środkowym. Następnie resztę elementów dzielimy na dwa podzbiory - w lewym będą wszystkie elementy równe lub mniejsze od środkowego, a w prawym wszystkie elementy większe od środkowego. Kolejność elementów wyznacza oczywiście funkcja porównująca wg następującej reguły:
D - zbiór sortowany
L - podzbiór lewy
P - podzbiór prawy
p - element środkowy należący do D
a - dowolny element zbioru D, różny od p
D = L { p } P
a L fp(a,p) = true
a P fp(p,a) = true
Jeśli element a jest równy p (co może się zdarzyć w zbiorach dopuszczających identyczne elementy), to nie ma znaczenia, w którym z podzbiorów go umieścimy (zwykle będzie to lewy podzbiór).
W następnym kroku identycznie sortujemy każdy z podzbiorów L i P otrzymując kolejne podzbiory. Operację tą wykonuje się rekurencyjnie wywołując procedurę szybkiego sortowania z danym podzbiorem. Sortowanie jest kontynuowane, aż sortowany podzbiór jest pusty lub zawiera tylko jeden element. Po złożeniu wszystkich podzbiorów w jeden otrzymujemy zbiór posortowany zgodnie z kryterium funkcji porównującej.
Przy sortowaniu bardzo istotny jest wybór elementu środkowego, który posłuży do podzielenia zbioru na dwa podzbiory. Jeśli element ten będzie wybrany nieprawidłowo, to efektywność algorytmu spadnie, nawet do poziomu O(n2) dla niektórych typów danych wejściowych - należy sobie zdawać z tego sprawę przy stosowaniu algorytmu szybkiego sortowania. Zwykle zaleca się przypadkowy wybór jednego z elementów zbioru, jednak taka implementacja algorytmu jest nieco kłopotliwa dla początkujących adeptów sztuk programowania. My zastosujemy inny sposób - jako element środkowy będziemy wybierać ostatni element sortowanego zbioru - jest to dobre rozwiązanie, o ile zbiór wejściowy nie jest wstępnie posortowany w kolejności odwrotnej, wtedy mogą być kłopoty!. Podzbiory będą budowane w zbiorze sortowanym, co znakomicie zaoszczędzi wykorzystywaną przez algorytm pamięć operacyjną komputera.
Przykład
Posortujemy tą metodą zbiór dziesięciu liczb: { 9 7 4 5 0 6 3 2 1 8 } w porządku rosnącym. Nasza funkcja porównująca przyjmie więc postać relacji mniejszy lub równy.
{ 9 7 4 5 0 6 3 2 1 8 } |
Na element środkowy wybieramy ostatni element zbioru - liczbę 8 |
{ 7 4 5 0 6 3 2 1 } 8 { 9 } |
Zbiór dzielimy na dwa podzbiory zawierające odpowiednio elementy mniejsze i większe od wybranego elementu środkowego. Prawy podzbiór jest już posortowany, ponieważ zawiera tylko jeden element - liczbę 9. Przechodzimy do sortowania lewego zbioru. |
{ 7 4 5 0 6 3 2 1 }{ 8 9 } |
Wybieramy ostatni element - liczbę 1. |
{ 0 } 1 {7 4 5 6 3 2 }{ 8 9 } |
Dzielimy zbiór wg wybranego elementu środkowego na dwa podzbiory. Podzbiór lewy jest już posortowany, ponieważ zawiera tylko jeden element - liczbę 0. |
{ 0 1 }{7 4 5 6 3 2 }{ 8 9 } |
Wybieramy w podzbiorze prawym element środkowy - liczbę 2. |
{ 0 1 }{ } 2 { 7 4 5 6 3 }{ 8 9 } |
Dokonujemy podziału zbioru na dwa podzbiory względem wybranego elementu. Lewy podzbiór jest teraz pusty. |
{ 0 1 2 }{ 7 4 5 6 3 }{ 8 9 } |
Wybieramy element środkowy. |
{ 0 1 2 }{ } 3 { 7 4 5 6 }{ 8 9 } |
Lewy podzbiór znów pusty. |
{ 0 1 2 3 }{ 7 4 5 6 }{ 8 9 } |
Wybieramy element środkowy |
{ 0 1 2 3 }{ 4 5 } 6 { 7 }{ 8 9 } |
Prawy podzbiór jest posortowany, ponieważ zawiera tylko jeden element. |
{ 0 1 2 3 }{ 4 5 }{ 6 7 8 9 } |
Wybieramy element środkowy |
{ 0 1 2 3 }{ 4 } 5 { }{ 6 7 8 9 } |
Lewy i prawy podzbiór posortowany. |
{ 0 1 2 3 4 5 6 7 8 9 } |
Ponieważ nie ma więcej podzbiorów, zbiór wejściowy został w całości posortowany. |
Dzielenie zbioru na dwa podzbiory
Kluczowym elementem szybkiego sortowania jest podział zbioru na dwa podzbiory. Sprecyzujmy zadanie następująco:
Mamy zbiór elementów { am, am+1, am+2, ... , an-1, an }, gdzie indeks m określa pierwszy element, a indeks n ostatni i oczywiście m < n. Takie określenie elementów pozwoli nam w dalszej części opracowania sortować wybraną część zbioru wejściowego. Jako element środkowy przyjmujemy początkowo element ostatni o indeksie n, czyli p = n. Element ten posłuży do wyznaczenia dwóch podzbiorów - lewego o indeksach mniejszych od p z elementami mniejszymi od środkowego oraz prawego o indeksach większych od p z elementami większymi. Celem naszego algorytmu będzie uzyskanie takiego podziału zbioru wejściowego.
Umówmy się co do sposobu oznaczania tych podzbiorów. Zrobimy to przy pomocy trzech liczb określających indeksy:
m - indeks pierwszego elementu - wartość stała
n - indeks ostatniego element - wartość stała
p - indeks elementu środkowego - wartość zmienna
Przy tej umowie elementy należące do lewego podzbioru (elementy mniejsze od środkowego) będą miały indeksy od m do p-1. Zbiór ten jest pusty, jeśli m = p. Indeksy prawego podzbioru (elementy większe od środkowego) będą miały indeksy od p+1 do n. Zbiór ten jest pusty, gdy p = n:
L = { am, am+1, ..., ap-2, ap-1 }, gdy m < p
L = { }, gdy m = p
P = { ap+1, ap+2, ... ,an-1, an }, gdy p < n
P = { }, gdy p = n
Podział zbioru rozpoczynamy od elementu przedostatniego o indeksie n-1 (element ostatni jest elementem środkowym). Element ten wyjmujemy ze zbioru (zapamiętujemy go w zmiennej pomocniczej). Jego pozycja jest teraz zwolniona (tzn. może zostać zapisana bez utraty poprzedniej zawartości, którą przechowuje zmienna pomocnicza). Następnie porównujemy wyjęty element z elementem środkowym. Jeśli jest on mniejszy lub równy elementowi środkowemu wg funkcji porównującej, to wstawiamy go z powrotem do zbioru (innymi słowy nic z nim nie robimy). W przeciwnym przypadku przesuwamy w lewo o 1 pozycję wszystkie elementy począwszy od następnego i skończywszy na elemencie środkowym. W wyniku tej operacji po prawej stronie elementu środkowego zwalnia się miejsce, w którym umieszczamy element wybrany (przepisujemy go ze zmiennej pomocniczej). Indeks elementu środkowego zmniejszamy o 1. Nad kolejnymi w dół elementami zbioru wykonujemy identyczne operacje aż dojdziemy do elementu o indeksie m. Wtedy zbiór wejściowy zostanie podzielony na dwa podzbiory. Oto odpowiedni przykład:
Przykład
Podzielimy zbiór wejściowy { 3 2 8 6 4 7 5 } na dwa podzbiory - lewy z liczbami mniejszymi od elementu ostatniego - 5 oraz prawego z liczbami większymi od tej wartości.
{ 3 2 8 6 4 7 5 } |
Elementem środkowym podziału jest ostatni element zbioru wejściowego - liczba 5. |
7 |
Ze zbioru wyjmujemy przedostatni element - liczbę 7 i porównujemy ją z elementem środkowym. |
7 |
Ponieważ liczba ta jest większa od elementu środkowego, dokonujemy przesunięcia o 1 pozycję w lewo wszystkich elementów począwszy od następnego (tutaj nie występuje) a skończywszy na elemencie środkowym. Indeks p jest zmniejszany o 1, aby wskazywał nową pozycję elementu środkowego w zbiorze. Po prawej stronie utworzyło się w wyniku przesunięcia puste miejsce. |
{ 3 2 8 6 4 5 7 } |
W miejsce to wstawiamy wybrany poprzednio element - liczbę 7. |
4 |
Wybieramy kolejny w dół element zbioru - liczbę 4 i porównujemy ją z elementem środkowym. Ponieważ liczba 4 jest mniejsza od 5, pozostawiamy ją na swoim miejscu. |
6 |
Wybieramy kolejny w dół element i porównujemy go z elementem środkowym. |
6 |
Ponieważ 6 jest większe od elementu środkowego, przesuwamy w lewo o 1 pozycję wszystkie elementy następne do elementu środkowego włącznie. Indeks p jest zmniejszany o 1. |
{ 3 2 8 4 5 6 7 } |
Na zwolnionym miejscu po prawej stronie elementu środkowego wstawiamy liczbę 6. |
8 |
Przechodzimy do następnego w dół elementu zbioru - liczby 8 i porównujemy ją z elementem środkowym - liczbą 5. |
8 |
Ponieważ 8 jest większe od 5, przesuwamy w lewo o 1 pozycję elementy od następnego do środkowego włącznie. Indeks p jest zmniejszany o 1. |
{ 3 2 4 5 8 6 7 } |
Na zwolnione miejsce wstawiamy liczbę 8. |
2 |
Liczbę 2 pozostawiamy na swojej pozycji, ponieważ jest mniejsza od elementu środkowego. |
3 |
To samo dotyczy liczby 3. |
{ 3 2 4 5 8 6 7 } |
Zbiór wejściowy został podzielony na dwa podzbiory : L = { 3 2 4 } z elementami mniejszymi od 5 oraz P = { 8 6 7 } z elementami większymi od 5. |
Schemat blokowy podziału podziału zbioru na dwa podzbiory
Dany jest zbiór { am am+1 am+2 ...an-2 an-1 an }, który należy podzielić na dwa podzbiory względem elementu środkowego an. Porządek wyznacza funkcja porównująca fp(...). Do opisu algorytmu stosujemy następujące zmienne:
m |
indeks pierwszego elementu zbioru wejściowego |
n |
indeks ostatniego elementu zbioru wejściowego |
p |
indeks elementu środkowego |
t |
zmienna pomocnicza do przechowywania wartości tymczasowych |
i,j |
zmienne liczników pętli |
a[...] |
element zbioru o podanym indeksie |
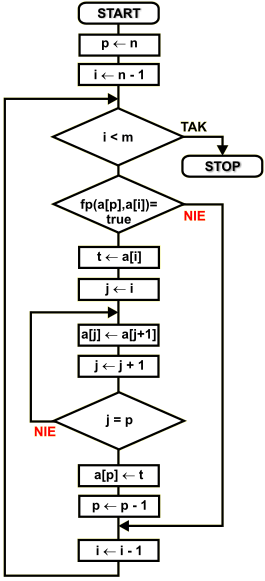
Punkt podziałowy p znajduje się na końcu zbioru. Do zmiennej p wprowadzamy więc indeks ostatniego elementu zbioru. Następnie będziemy przeglądać kolejno w dół wszystkie elementy o indeksach od n-1 do m i porównywać je z elementem środkowym a[p]. Jeśli będą one większe ze względu na funkcję porównującą, to dokonamy odpowiedniego przesunięcia elementów w lewo i wstawienia porównywanego elementu za element środkowy. Indeks porównywanych elementów przechowuje zmienna i. Na początku wpisujemy do niej indeks przedostatniego elementu, czyli n-1.
Przed wykonaniem kolejnego obiegu pętli zewnętrznej sprawdzamy, czy indeks mieści się w zakresie. Jeśli nie, to kończymy.
Jeśli indeks i mieści się w zakresie (jest większy lub równy m), to sprawdzamy funkcją porównującą kolejność elementów a[i] oraz a[p]. Jeśli a[i] ma być po prawej stronie a[p], to zawartość elementu a[i] trafia do zmiennej pomocniczej t, a wszystkie elementy od indeksu i + 1 do p włącznie zostają przesunięte o 1 pozycję w lewo. Dzięki tej operacji element o indeksie p zostaje zwolniony - oryginalny element środkowy a[p] jest teraz na pozycji o 1 mniejszej, czyli a[p-1].
Do zwolnionego elementu a[p] wpisujemy zawartość zmiennej pomocniczej, czyli oryginalny element a[i].
Indeks p zmniejszamy o 1, aby prawidłowo wskazywał pozycję elementu środkowego.
Przechodzimy do kolejnego w dół elementu zbioru i kontynuujemy pętlę zewnętrzną.
Algorytm Sortowania Szybkiego
Procedura sortowania szybkiego jest procedurą rekurencyjną z parametrami określającymi zakres indeksów sortowanego zbioru. Rekurencja ma to do siebie, iż procedura (lub funkcja) wywołuje samą siebie. Takie wywołanie powoduje przesłanie na stos wszystkich argumentów procedury podanych w wywołaniu. Nowy egzemplarz tej procedury będzie więc pracował z niezależnym zestawem danych. Algorytm sortujący możemy opisać słownie tak:
Procedura QSrt(ip,ik) - parametry ip i ik określają indeksy pierwszego i ostatniego elementu do sortowania w zbiorze wejściowym i są przekazywane poprzez stos.
Podziel zadany zbiór wejściowy na dwa podzbiory względem ostatniego elementu, który będzie elementem środkowym podziału. W lewym podzbiorze umieść wszystkie elementy mniejsze lub równe elementowi środkowemu. W prawym podzbiorze umieść wszystkie elementy większe od elementu środkowego.
Jeśli lewy podzbiór ma więcej niż jeden element, to wywołaj procedurę QSrt(ip,p-1). Nowy egzemplarz procedury będzie pracował z parametrami ip' = ip oraz ik' = p-1
Jeśli prawy podzbiór ma więcej niż jeden element, to wywołaj procedurę QSrt(p+1,ik). Nowy egzemplarz procedury będzie pracował z parametrami ip' = p + 1 oraz ik' = ik.
Zakończ działanie procedury
Jeśli chcemy posortować cały zbiór { a1 a2 ... an-1 an }, to w programie należy wywołać procedurę jako QuickSort(1,n). Wywołanie to zainicjuje kolejne podziały zbioru aż do jego posortowania.
Poniżej przedstawiamy realizację opisanego algorytmu sortowania w różnych językach programowania. Program tworzy dwie tablice o identycznej zawartości, wypełnione przypadkowymi liczbami. Następnie jedną z tych tablic sortuje i wyświetla obie dla zobrazowania efektu posortowania danych.
Przykład w C++
Wszystkie prezentowane tutaj przykłady zostały uruchomione w DevC++, który można darmowo i legalnie pobrać poprzez sieć Internet.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 15; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
// rekurencyjna funkcja szybkiego sortowania
void qsrt(int ip, int ik, int * a)
{
int i,j,t,p;
p = ik;
for(i = ik - 1; i >= ip; i--)
{
if(fp(a[p],a[i]))
{
t = a[i];
for(j = i; j < p; j++) a[j] = a[j+1];
a[p--] = t;
};
};
if(p - ip > 1) qsrt(ip, p - 1, a);
if(ik - p > 1) qsrt(p + 1, ik, a);
}
// główna funkcja programu
int main()
{
int i,a[n],b[n];
// tworzymy tablicę z przypadkową zawartością.
// tablica b[] służy do zapamiętania stanu a[]
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ ) a[i] = b[i] = 1 + rand() % (n + n);
// wywołujemy funkcję szybkiego sortowania z pełnym zakresem indeksów
qsrt(0,n-1,&a[0]);
// wyświetlamy wyniki
cout << "Sortowanie szybkie" << endl
<< "(C)2003 mgr Jerzy Walaszek" << endl << endl
<< " lp przed po" << endl
<< "------------------------" << endl;
for(i = 0; i < n; i++)
{
cout.width(4); cout << i + 1;
cout.width(9); cout << b[i];
cout.width(9); cout << a[i] << endl;
};
cout << endl;
cout.flush();
system("pause");
return 0;
}
Wyszukiwanie Binarne
Binary Search
Wyszukiwanie danych jest zagadnieniem spokrewnionym z sortowaniem. Jeśli zbiór nie jest posortowany i chcemy w nim znaleźć element spełniający określone kryterium, to musimy przeglądać kolejne elementy aż natrafimy na właściwy. Jeśli danego elementu w zbiorze nie ma, odpowiedź otrzymamy dopiero po przeglądnięciu całego zbioru. Przy dużym zbiorze może zająć to nam sporo czasu. Taki rodzaj przeszukiwania nosi nazwę liniowego i ma złożoność obliczeniową klasy O(n).
Dużo efektywniejsze jest przeszukiwanie zbiorów posortowanych, gdyż wtedy nie musimy sprawdzać wszystkich elementów, lecz możemy skorzystać z własności tej, iż kolejne elementy zbioru są umieszczone w nim zgodnie z określonym porządkiem (zdefiniowanym np. przez funkcję porównującą). Dla takich zbiorów można zastosować algorytm wyszukiwania binarnego. Zasada jest następująca. W zbiorze wybieramy element środkowy. Ponieważ zbiór jest posortowany, to mamy pewność, iż na lewo są elementy mniejsze (lub równe), a na prawo są elementy większe wg funkcji porównującejj. Sprawdzamy, czy element ten spełnia kryteria poszukiwań. Jeśli tak, to kończymy (tylko jedno porównanie!). Jeśli nie, to sprawdzamy, czy element środkowy jest większy lub mniejszy od poszukiwanego. Jeśli jest większy, to poszukiwany element znajduje się w lewej połówce. Analogicznie jeśli element środkowy jest mniejszy, to poszukiwany element będzie się znajdował w prawej połówce. Wybieramy więc jedną z połówek za nowy zbiór do przeszukania. Jest on o połowę mniej liczny od zbioru wyjściowego. Całą operację powtarzamy z połówką zbioru. Jeśli nie znajdziemy poszukiwanego elementu, to znów dostaniemy dwie połówki - czterokrotnie mniejsze od zbioru wyjściowego. Wybieramy jedną z nich zgodnie z podaną regułą i kontynuujemy aż do znalezienia elementu lub otrzymania połówek, których już dalej nie można dzielić - wtedy wiemy, że poszukiwanego elementu w zbiorze nie ma.
Zwróć uwagę, iż po każdym porównaniu liczebność zbioru maleje o połowę. Umożliwia to szybkie i efektywne wyszukanie elementu nawet w olbrzymim zbiorze danych. Oto odpowiedni przykład.
Przykład
Chcemy wyszukać za pomocą opisanego algorytmu liczbę 14 w zbiorze { 2 3 5 6 7 9 10 14 16 25 30 }.
1 2 3 4 5 6 7 8 9 10 11 |
Najpierw znajdujemy element środkowy. Możemy obliczyć jego indeks jako średnią arytmetyczną indeksu pierwszego i ostatniego elementu zbioru. Oczywiście wynik zaokrąglamy do wartości całkowitej. (1+11)/2 = 6. Szóstym elementem jest liczba 9, którą oznaczyliśmy na czerwono. |
1 2 3 4 5 6 7 8 9 10 11 |
Teraz sprawdzamy, czy element środkowy jest równy poszukiwanemu. U nas nie jest. Skoro nie jest równy, to musi być większy lub mniejszy od poszukiwanego. U nas jest mniejszy, więc dalsze poszukiwania będziemy prowadzić w prawej połówce. |
1 2 3 4 5 6 7 8 9 10 11 |
Obliczamy nowy indeks elementu środkowego, który jest równy: (7+11)/2 = 9. Element środkowy zaznaczyliśmy na czerwono. Jest to liczba 16. |
1 2 3 4 5 6 7 8 9 10 11 |
Sprawdzamy, czy poszukiwany element jest równy elementowi środkowemu. Nie jest. Element środkowy jest większy, więc przenosimy się do lewej połowy. |
1 2 3 4 5 6 7 8 9 10 11 |
Indeks elementu środkowego = (7+8)/2 = 7. Jest to liczba 10 zaznaczona na czerwono. |
1 2 3 4 5 6 7 8 9 10 11 |
Porównujemy. Element środkowy jest mniejszy, przenosimy się do prawej połówki. |
1 2 3 4 5 6 7 8 9 10 11 |
Znajdujemy element środkowy - (8+8)/2 = 8. Jest to liczba 14. Porównanie da teraz wynik pozytywny. |
Ile operacji porównań wykonano? Cztery. A więc bardzo szybko znaleźliśmy pozycję elementu w zbiorze posortowanym. Teraz zobaczmy, co się dzieje, gdy poszukiwanego elementu w zbiorze nie ma. Spróbujemy znaleźć w tym samym zbiorze danych liczbę 4.
1 2 3 4 5 6 7 8 9 10 11 |
Znajdujemy element środkowy. |
1 2 3 4 5 6 7 8 9 10 11 |
Element środkowy większy od poszukiwanej liczby, przenosimy się do lewej połówki zbioru. |
1 2 3 4 5 6 7 8 9 10 11 |
Znajdujemy element środkowy. |
1 2 3 4 5 6 7 8 9 10 11 |
Element środkowy większy. Wybieramy lewą połówkę. |
1 2 3 4 5 6 7 8 9 10 11 |
Znajdujemy element środkowy. |
1 2 3 4 5 6 7 8 9 10 11 |
Element środkowy mniejszy od poszukiwanego. Wybieramy prawą połówkę. |
1 2 3 4 5 6 7 8 9 10 11 |
Znajdujemy element środkowy: |
1 2 3 4 5 6 7 8 9 10 11 |
Element środkowy mniejszy od poszukiwanego. Ponieważ zbiór jest jednoelementowy, to nie można go już podzielić na dwie rozłączne połowy. Przeszukanie zostaje więc zakończone z wynikiem negatywnym - poszukiwanego elementu w zbiorze nie ma. |
Ile wykonano porównań? Cztery. Ponieważ zbiór po każdym porównaniu jest dzielony na coraz mniejsze podzbiory, to maksymalna liczba porównań w n-elementowym zbiorze posortowanym wyniesie nie więcej niż |log2n|+1. Wobec tego możemy oszacować złożoność obliczeniową algorytmu wyszukiwania binarnego na O(log2n). Jest to złożoność mniejsza od liniowej O(n), a więc bardzo korzystna (np. szesnastokrotny wzrost liczby danych powoduje jedynie czterokrotny wzrost czasu wyszukiwania).
Schemat blokowy
Dany jest zbiór { a1 a2 a3 ...an-2 an-1 an } oraz element x, który należy w zbiorze odszukać. Zbiór jest posortowany zgodnie z kryterium zdefiniowanym przez funkcję porównującą. Do opisu algorytmu stosujemy następujące zmienne:
n |
liczba elementów w zbiorze |
a[...] |
element zbioru o numerze od 1 do n podanym w klamrach kwadratowych |
f |
zmienna logiczna informująca o wyniku poszukiwań. Wartość true oznacza znalezienie elementu, wartość false informuje, iż poszukiwanego elementu w zbiorze nie ma |
p |
zmienna przechowująca indeks elementu środkowego. Po zakończeniu działania algorytmu w zmiennej tej znajdzie się indeks poszukiwanego elementu, jeśli f=true |
x |
poszukiwany element |
ip,ik |
zmienne przechowują indeksy elementu początkowego i końcowego przeszukiwanych zbiorów |
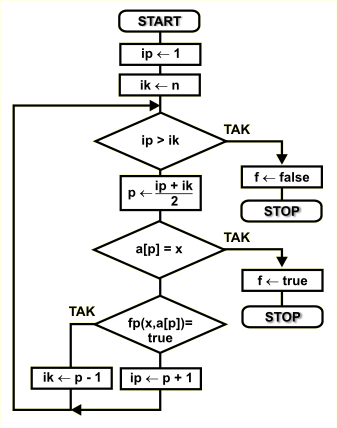
Zakres poszukiwań definiują dwie zmienne - ip zawierająca indeks pierwszego elementu oraz ik zawierająca indeks ostatniego elementu zbioru. Na początku algorytmu inicjujemy je odpowiednio na pierwszy i ostatni element w zbiorze wejściowym.
Jeśli w trakcie działania algorytmu dojdzie do sytuacji, gdy indeks początkowy jest większy od końcowego, to oznacza to zbiór pusty. W takim przypadku kończymy działanie algorytmu z wynikiem negatywnym - poszukiwanego elementu w zbiorze wejściowym nie ma - zmienna f przyjmie wartość false.
Jeśli zakres jest w porządku, to obliczamy indeks elementu środkowego, który wyznaczy dwie połówki zbioru. Indeks ten obliczamy jako średnią arytmetyczną indeksów ip oraz ik, zaokrągloną do wartości całkowitej.
Sprawdzamy, czy element środkowy o indeksie p jest poszukiwanym elementem. Jeśli tak, to kończymy z wynikiem pozytywnym - zmienna p zawiera pozycję odszukanego elementu.
W przypadku, gdy poszukiwany element nie jest równy elementowi środkowemu, musi się on znajdować w jednej z dwóch połówek, które wyznacza element środkowy. Dalsze poszukiwania będziemy prowadzić w lewej połówce, jeśli ze względu na kolejność wyznaczoną przez funkcję porównującą poszukiwany element jest przed elementem środkowym (czyli fp(x,a[p]) = true) lub w połówce prawej w sytuacji przeciwnej. Przy przejściu do połówki lewej indeks końcowy ustawiamy na wartość o jeden mniejszą od indeksu p, a w prawej połówce indeks początkowy ip ustawiamy na wartość o jeden większą od p. Eliminuje to z połówek element środkowy, który już nie musi być brany pod uwagę. Również w sytuacji, gdy któraś z połówek jest zbiorem pustym, powoduje to, iż wyrażenie ip > ik stanie się prawdziwe i algorytm zakończy się z wynikiem negatywnym.
Poniżej przedstawiamy realizację opisanego algorytmu wyszukiwania binarnego w różnych językach programowania. Przedstawiony program najpierw tworzy tablicę n przypadkowych liczb. Następnie sortuje ją metodą przez wstawianie. W wyniku posortowania w pierwszym elemencie znajduje się wartość najmniejsza, a w ostatnim największa. Na podstawie tych dwóch wartości program generuje liczbę przypadkową wpadającą w zakres liczb w tablicy. Za pomocą algorytmu wyszukiwania binarnego zostaje znaleziona pozycja wygenerowanej liczby i wyniki są wyświetlane na ekranie.
Przykład w C++
Wszystkie prezentowane tutaj przykłady zostały uruchomione w DevC++, który można darmowo i legalnie pobrać poprzez sieć Internet.
#include <stdlib.h>
#include <time.h>
#include <iostream.h>
const int n = 10; // liczba elementów w sortowanym zbiorze
// funkcja porównująca
int fp(int x, int y)
{
return (x <= y);
}
int main()
{
int i,j,ip,ik,p,t,x,a[n];
cout << "Demonstracja przeszukiwania binarnego" << endl
<< " (C)2003 mgr Jerzy Walaszek" << endl << endl;
// tworzymy tablicę z przypadkową zawartością.
srand( (unsigned)time( NULL ) );
for(i = 0; i < n; i++ ) a[i] = rand() % n;
// tablicę sortujemy metodą przez wstawianie
for(i = n - 2; i >= 0; i--)
{
t = a[i];
for(j = i + 1; (j < n) && !fp(t,a[j]); j++) a[j - 1] = a[j];
a[j - 1] = t;
};
// wyznaczamy poszukiwany element na podstawie wartości
// minimalnej i maksymalnej w tablicy a[]
x = a[0] + rand() % (a[n-1] - a[0] + 1);
cout << "Liczba " << x << " w zbiorze posortowanym" << endl << endl;
for(i = 0; i < n; i++)
cout << "a[" << i << "] = " << a[i] << endl;
// znajdujemy pozycję elementu x w tablicy a[]
ip = 0; ik = n-1;
while(ip <= ik)
{
p = (ip + ik) / 2;
if(a[p] == x) break;
if(fp(x,a[p]))
ik = p - 1;
else
ip = p + 1;
};
// wyświetlamy wyniki. Jeśli element został znaleziony, to ip <= ik
// i p zawiera jego pozycję. W przeciwnym razie ip > ik - elementu
// nie znaleziono.
if(ip <= ik)
cout << endl << "znajduje sie na pozycji " << p << endl;
else
cout << endl << "nie wystepuje" << endl;
// czekamy na naciśnięcie klawisza i kończymy program
cout << endl;
cout.flush();
system("pause");
return 0;
}
Wyszukiwarka
Podobne podstrony:
Zadania na komis 2001, ZiIP, 2 sem, Informatyka, Egzaminy
tyszer2, ZiIP, 2 sem, Informatyka, Egzaminy
ZADANIA Z EGZAMINU PODSTAWY INFORMATYKI, ZiIP, 2 sem, Informatyka, Egzaminy
Egzam info, ZiIP, 2 sem, Informatyka, Informatyka
EGZAMIN Z PRZETWÓRSTWA TWORZYW SZTUCZNYCH 25, ZiIP, sem 2
Pytania egzamin systemy sem I, INFORMATYKA, Sieci, S O i S K I sem
ALS - 009-005 - Program Sortowanie INSERTION SORT, Informatyka - uczelnia, WWSI i WAT, wwsi, SEM II,
PRZYKŁADOWE ZADANIA EGZAMINACYJNE zip- Is, ZiIP, sem 1
ZAGADNIENIA EGZAMINACYJNE-zip, ZiIP, sem 2
pytania egzamin op(1), ZiIP sem.I, OP
pytania egzamin op, ZiIP, sem 1, Obróbka plastyczna, Obóbka plastyczna-egz
Pytania egzamin z odlewnictwa, ZiIP, sem 2
EGZAMIN Z PRZETWÓRSTWA TWORZYW SZTUCZNYCH 25, ZiIP, sem 2
Spr. 4-Techniki wytw, ZiIP, sem 1
Sprawozdanie z laboratorium obróbki plastycznej, ZiIP, sem 1
inf, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
Plan z 1 sem, INFORMATYKA SEM 1, Plan lekcji
Informator o egzaminie zawodowym potwierdzającym kwalifikacje zawodowe errata
więcej podobnych podstron