![]()
(1)
Sprawozdanie z ćwiczenia laboratoryjnego
Wyznaczanie współczynnika filtracji
Grupa 3
Rok akademicki 2005/2006
Skład zespołu:
Adam Kotarski
Radosław Szczygielski
Tomasz Milewski
Szczecin, 12 stycznia 2006
Wstęp teoretyczny
W ćwiczeniu laboratoryjnym należało wyznaczyć współczynnik filtracji dla ośrodka gruntowego, z którego był usypany modelowy wał przeciwpowodziowy.
Współczynnik filtracji (oznaczany jako k) zależy od rodzaju gruntu (uziarnienia, struktury i porowatości) oraz od lepkości przepływającej cieczy. Współczynnik ten zwany jest także stałą Darcy'ego, od nazwiska francuskiego inżyniera, który na podstawie doświadczeń określił prędkość cieczy w porach gruntu.
![]()
(1)
gdzie:
v - prędkość cieczy w porach gruntu
k - współczynnik filtracji [m/s]
J - spadek zwierciadła wody [liczba niemianowana]
Jeśli narysujemy wykres poziomu cieczy w gruncie, możemy wyznaczyć spadek J zwierciadła wody.
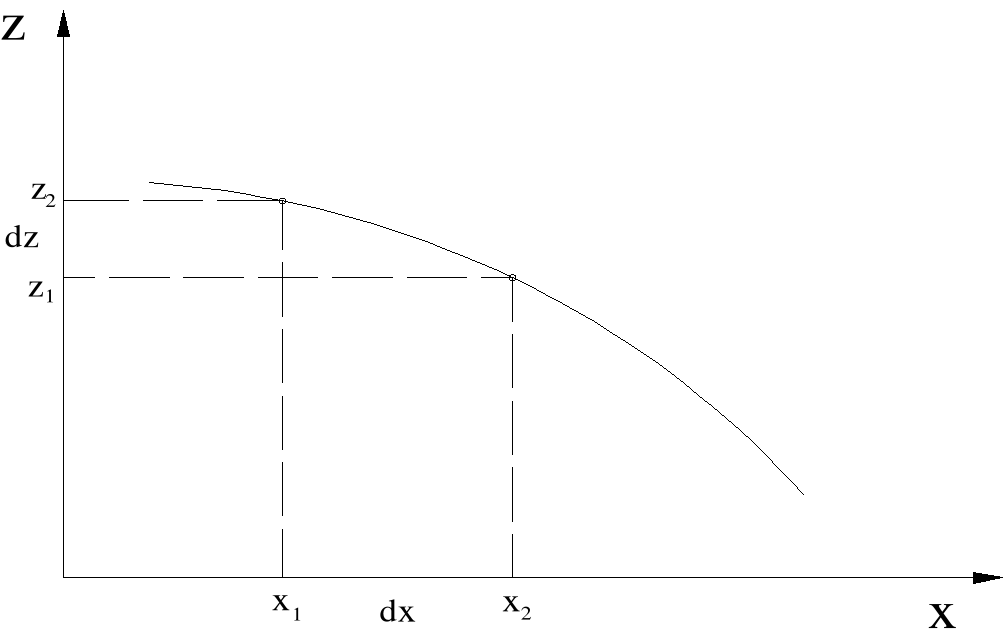
![]()
(2)
Jeśli podstawimy to do wzoru (1) otrzymamy:
![]()
(3)
Ta postać wzoru na prędkość filtracji cieczy, jest zwana wzorem Dupuit.
Ponieważ w naszym przypadku mamy do czynienia funkcją malejącą, musimy zmienić znak na przeciwny.
![]()
(4)
Wiedząc, że:
![]()
![]()
oraz
![]()
i podstawiając do wzoru (4), otrzymamy:
![]()
po rozdzieleniu zmiennych
![]()
i po scałkowaniu w granicach x1, x2 dla zmiennej x i z1, z2 dla zmiennej z
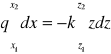
otrzymamy
![]()
czyli
![]()
![]()
W ten sposób znając wysokości poziomów wody w gruncie i odległości od tych poziomów, możemy wyznaczyć współczynnik filtracji.
Schemat ideowy stanowiska doświadczalnego
3. Przebieg doświadczenia
pomierzyć geometryczne parametry stanowiska
otworzyć dopływ wody do stanowiska i odczekać aż woda podniesie się do określonego poziomu przed wałem
zmierzyć natężenie przepływu metodą wolumetryczną
pomierzyć poziomy wody w piezometrach
pomiar powtórzyć przy innym poziomie wody przed wałem
4. Wyniki doświadczenia
Nr piezometr. |
Hi [cm] |
V [cm3] |
t[s] |
b[cm] |
q [cm2/s] |
ki[cm/s] |
8 |
31,0 |
513 515 512 |
45 |
10,7 |
0,778 |
2,88 |
9 |
29,7 |
|
|
|
|
2,19 |
10 |
27,9 |
|
|
|
|
2,01 |
11 |
25,8 |
|
|
|
|
3,02 |
12 |
24,3 |
|
|
|
|
2,13 |
13 |
22,0 |
|
|
|
|
2,37 |
14 |
19,7 |
|
|
|
|
2,56 |
15 |
17,3 |
|
|
|
|
2,94 |
16 |
14,9 |
|
|
|
|
3,21 |
17 |
12,3 |
|
|
|
|
2,75 |
18 |
8,3 |
|
|
|
|
|
Nr piezometr. |
Hi [cm] |
V [cm3] |
t[s] |
b[cm] |
q [cm2/s] |
ki[cm/s] |
8 |
31,0 |
331,2 330 332,8 |
45 |
10,7 |
1,136 |
2,71 |
9 |
29,7 |
|
|
|
|
2,16 |
10 |
27,9 |
|
|
|
|
1,97 |
11 |
25,8 |
|
|
|
|
2,90 |
12 |
24,3 |
|
|
|
|
2,60 |
13 |
22,0 |
|
|
|
|
2,47 |
14 |
19,7 |
|
|
|
|
2,84 |
15 |
17,3 |
|
|
|
|
3,17 |
16 |
14,9 |
|
|
|
|
3,72 |
17 |
12,3 |
|
|
|
|
3,86 |
18 |
8,3 |
|
|
|
|
|
6. Analiza błędów
W doświadczeniu można było popełnić wiele błędów pomiarowych. Dotyczy to zarówno pomiaru wydatku, jak i zmierzenia geometrycznych parametrów stanowiska. W pomiarach przyjęliśmy, że szerokość przekroju wału jest równa odległości od ścianek naczynia w jego górnej części. To założenie może być błędne, zatem wyniki nie mogą być miarodajne.
7. Wnioski
Wyznaczone przez nas współczynniki filtracji różniły się od siebie w poszczególnych przekrojach. Może to świadczyć o niejednorodności gruntu lub po prostu o popełnionych przez nas błędach pomiarowych. Średnia wartość współczynnika filtracji była rzędu 2,7 cm/s. Porównując tą wartość z wartościami z książki „Gruntoznawstwo budowlane” Jana Jeża (tablica 2.3) oraz „Hydraulika techniczna” Jana Kubraka, odczytujemy, że podobne wartości obliczono dla piasków grubych (1,5 - 5 cm/s). Potwierdza to fakt, że nasze wyniki są obarczone dużym błędem i nie możemy porównywać ich z wartościami dla rzeczywistych ośrodków porowatych.
Q - wydatek [m3/s]
A - pole powierzchni przekroju [m2]
B - szerokość przekroju [m]
z - wysokość przekroju [m]
Q - wydatek jednostkowy [m2/s]