Badania Operacyjne Wykład 02 2004-10-18

BADANIA OPERACYJNE zajmują się teorią podejmowania decyzji i rozwiązywania problemów

Ogólne sformułowanie zagadnienia programowania matematycznego:

Z problemem wyboru decyzji optymalnej ze względu na wybrany cel działania mamy do czynienia, gdy:

• istnieje ograniczona swoboda w podejmowaniu decyzji, dlatego też każda decyzja, która uwzględnia przyjęte ograniczenia będzie nazwana DECYZJĄ DOPUSZCZALNĄ

• istnieje możliwość podjęcia więcej niż jednej decyzji dopuszczalnej

• istnieje kryterium pozwalające ocenić stopień realizacji celu przez dowolną decyzję dopuszczalną. Decyzja dopuszczalna najlepiej realizująca przyjęty cel działania nazywa się DECYZJĄ OPTYMALNĄ

Podstawowe elementy modelu matematycznego dotyczącego problemu wyboru decyzji optymalnej i odzwierciedlających wybraną sytuację decyzyjną to:

a) zespół k - zmiennych x₁,x₂,…,x_k - zmienne decyzyjne

Każdy zestaw wartości x₁,x₂,…,x_k jest opisem ilościowym dowolnej decyzji, a zatem dla dowolnej decyzji wyznaczamy X = (x₁,x₂,…,x_k), a w interpretacji geometrycznej jest to pewien punkt w przestrzeni k - wymiarowej

(x₁,x₂,…,x_k) Є R^k

b) Dany jest zbiór D decyzji dopuszczalnych ograniczających swobodę podejmowania decyzji. Oznacza to, że nie każdy punkt przestrzeni k - wymiarowej reprezentuje decyzję dopuszczalną. Zbiór D jest podzbiorem zbioru R^k. D nie jest zbiorem pustym.

c) Dana jest funkcja f(x₁,x₂,…,x_k) = f(x)

Wartość funkcji wyznaczona dla dowolnej decyzji dopuszczalnej mierzy stopień realizacji celu przez tą decyzję. Dla dwóch różnych decyzji dopuszczalnych x₁,x₂ , x₁≠x₂, ta z nich lepiej realizuje przyjęty cel działania, dla której wartość funkcji jest taka sama, będziemy je traktować równorzędnie. Funkcja f ze względu na rolę jaką pełni w modelu matematycznym nazywa się funkcją celu albo funkcją kryterium.

Przyjmując powyższe założenia, za decyzją optymalną tzn. najlepiej realizującą przyjęty cel działania, uznamy tą spośród decyzji dopuszczalnych, dla której wartość funkcji celu jest max w zbiorze D.

dla

Jeżeli zbiór decyzji dopuszczalnych D zapiszemy w formie układu nierówności, jaki powinny spełniać wartości zmiennych decyzyjnych:

h₁ (x₁,x₂,…,x_k) ≤ b₁

h₂ (x₁,x₂,…,x_k) ≤ b₂

h_m (x₁,x₂,…,x_k) ≤ b_m

To wtedy problem wyboru decyzji optymalnej będziemy nazywać ZAGADNIENIEM PROGRAMOWANIA MATEMATYCZNEGO. A zatem zagadnienie programowania matematycznego, to każdy problem wyboru decyzji optymalnej, którego model matematyczny można zapisać, wyznaczyć wektor X=( x₁,x₂,…,x_k)

f(x₁,x₂,…,x_k) » max

Maksymalizujemy funkcję celu przy warunkach ograniczających

h_i (x₁,x₂,…,x_n) ≤ b_i i = (1,…,m)

Badania Operacyjne Wykład 03 2004-10-25

PROGRAM LINIOWY:

X = (x₁, x₂,…, x_k)

f(X) = c₁x₁ +c₂x₂ +…+ c_kx_k » max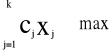

przy warunkach ograniczających:

a₁₁x₁ + a₁₂x₂ + … + a_1kx_k ≤ b₁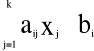
(i=1,…,m)

a₂₁x₁ + a₂₂x₂ + … + a_2kx_k ≤ b₂ x_j ≥ 0 (j=1,…,n)

……………………………………………….

a_m1x₁ + a_m2x₂ + … + a_mkx_k ≤ b_m

x_j ≥ 0 (j=1,…,n)

C^T » max

A_x ≤ b

x ≥ 0

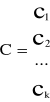
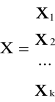
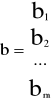
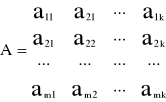
Jest to postać kanoniczna. Komplementarną formą jest postać standardowa.

POSTAĆ STANDARDOWA charakteryzuje się tym, że:

• warunki graficzne zapisane są w postaci równań

• wyrazy wolne poszczególnych warunków ograniczających są nieujemne

• warunki nieujemności są pełne tzn. dotyczą wszystkich zmiennych decyzyjnych

X = (x₁, x₂,…, x_k)

f(X) = c₁x₁ +c₂x₂ +…+ c_nx_n » max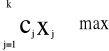

przy warunkach ograniczających:

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n = b₁ b₁ ≥ 0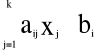
(i=1,…,m)

a₂₁x₁ + a₂₂x₂ + … + a_2kx_k = b₂ b₂ ≥ 0 b_i ≥ 0

…………………………………………. x_j ≥ 0 (j=1,…,n)

a_m1x₁ + a_m2x₂ + … + a_mnx_n = b_m b_m ≥ 0

x_j ≥ 0 (j=1,…,n)

C^T » max A_x ≤ b x ≥ 0 b ≥ 0 C,X Є Rⁿ A_mxn b Є R^m

METODY WYZNACZANIA ROZWIĄZANIA ZADANIA PROGRAMOWANIA LINIOWEGO:

1. metoda graficzna (geometryczna)

2. program dualny

3. metoda Simplex

Warunki stosowalności:

Metodę 1) można stosować tylko wtedy, jeśli w modelu znajdują się 2 zmienne decyzyjne (co najwyżej 3 zmienne). Jeśli w modelu programowania liniowego znajduję się więcej zmiennych decyzyjnych niż 2 (lub 3), natomiast liczba warunków ograniczających wynosi 2 (lub 3), to można wyznaczyć rozwiązanie takiego zadania programowania liniowego korzystając z zapisu programu dualnego w stosunku do programowania pierwotnego.

Metoda Simplex, która jest metodą uniwersalną, polegającą najogólniej biorąc na wyznaczeniu wstępnego rozwiązania bazowego, a następnie poprawianiu tego rozwiązania w kolejnych krokach iteracyjnych aż do uzyskania rozwiązania optymalnego, można stosować do wyznaczenia rozwiązania praktycznie rzecz biorąc każdego modelu PL (za wyjątkiem przypadków degenerowanych)

PROGRAM DUALNY:

Program pierwotny Program dualny

zmaksymalizować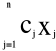
zminimalizować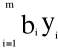

przy warunkach ograniczających: przy warunkach ograniczających:

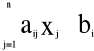
(i=1,…,m)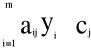
(j=1,…,n)

(j=1,…,n)
(i=1,…,m)

Program dualny jest w pewnym sensie transpozycją programu pierwotnego, a charakter tej transpozycji jest następujący:

1. j - ta kolumna współczynników stojących przy zmiennych decyzyjnych w warunkach ograniczających PP staję się i - tym wierszem współczynników w warunkach ograniczających PD

2. wektor ograniczeń zagadnienia pierwotnego przejmuje rolę współczynników funkcji celu w PD

3. współczynniki funkcji celu PP stają się wektorem wyrazów wolnych w PD

4. rodzaj optymalizacji oraz kierunki nierówności w warunkach ograniczających są przeciwne względem siebie w obu zagadnieniach

TWIERDZENIE 1

Jeżeli zagadnienie pierwotne i dualne mają rozwiązania dopuszczalne a
stanowi rozwiązanie optymalne zagadnienia pierwotnego, natomiast
stanowi rozwiązanie optymalne zagadnienia dualnego, to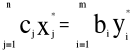
, co oznacza, że wartość funkcji celu zagadnienia pierwotnego i dualnego jest taka sama.

TWIERDZENIE 2

Jeżeli program pierwotny (dualny) ma skończone rozwiązanie optymalne to adekwatnie do niego program dualny (pierwotny) ma również rozwiązanie optymalne o tej samej wartości funkcji celu.

Badania Operacyjne

Wykład 04 2004-11-08

PROGRAM DUALNY - ZADANIE

Program Pierwotny:

x₁,…,x₄ ≥ 0

warunki ograniczające:

x₁+2x₂+1,5x₃+6x₄ ≤ 90000

2x₁+2x₂+1,5x₃+4x₄ ≤ 120000

funkcja:

f(x₁,…,x₄) = 4x₁+6x₂+3x₃+12x₄ » max

Program Dualny:

a) y₁+2y₂ ≥ 4 (4;0) (0;2)

b) 2y₁+2y₂ ≥ 6 (3;0) (0;3)

c) 1,5y₁+1,5y₂ ≥ 3 (2;0) (0;2)

d) 6y₂+4y₂ ≥ 12 (2;0) (0;3)

y₁,y₂ ≥ 0

f(y₁,y₂) = 90000y₁ + 120000y₂ » min

ZRD - Zbiór rozwiązań dopuszczalnych

90000y₂ + 120000y₂ = 360000 (4;0) (0;3)

Q - rozwiązanie optymalne PD

y₁+2y₂ = 4

2y₁ + 2y₂ =6

-y₁-2y₂ = -4

2y₁ +2y₂ =6

y₁ = 2

y₂ = 1 Q = (2;1)

Wartość funkcji celu wynosi:

f (2;1) = 90000 ∙ 2 + 120000 ∙ 1 = 180000 + 120000 = 300000

	Y1	Y2	F (y1,y2)
P	0	3	360 000
Q	2	1	300 000
S	4	0	360 000

Punkt Q stanowi rozwiązanie optymalne PROGRAMU DUALNEGO, a wartość funkcji celu jest wtedy minimalna i wynosi 300000

Po podstawieniu rozwiązania optymalnego Programu dualnego do warunków ograniczających programu dualnego otrzymujemy:

x₃* = x₄* = 0

x₁+2x₂ = 90000

2x₁ +2x₂ = 120000

x₂* = 30000

x₁* = 30000

Rozwiązaniem optymalnym PROGRAMU PIERWOTNEGO jest wektor, którego elementami są :

x₁* = 30000, x₂* = 30000, x₃* = 0, x₄* = 0. Wartość funkcji celu jest wtedy max i wynosi:

f (30000;30000) = 4 ∙ 30000 + 6 ∙ 30000 + 3 ∙ 0 + 12 ∙ 0 = 120000 +180000 + 0 + 0 = 300000

Praca pochodzi z serwisu www.e-sciagi.pl <<<>>> Zacznij zarabiać http://partner.e-sciagi.pl

---