Grupy 6 i 8 ZADANIA Z ALGEBRY (na 7 marca)

1. Proszę udowodnić indukcyjnie, że suma ciągu arytmetycznego o pierwszym wyrazie równym
i różnicy

a, a+r, a+2r,.....,a+nr,....

obliczona do wyrazu a+nr włącznie, wynosi

.

2. Proszę udowodnić, że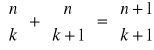

3. Proszę dowieść indukcyjnie, że .

Wskazówka: Należy oczywiście zdecydować, czy indukcję prowadzimy względem m, czy

względem n. Należy spróbować obydwu tych możliwości i sprawdzić, która wersja

dowodu może być pomyślnie doprowadzona do końca.

xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

Proszę zapoznać się z poniższym opracowaniem i rozwiązać zadania.

Liczby zespolone

Matematyka zaczęła się od liczb naturalnych, które służyły do liczenia przedmiotów. W zbiorze liczb naturalnych wprowadza się znane ze szkoły działania, które wymuszają rozszerzanie zbioru liczb: odejmowanie zmusza do wprowadzenia liczb ujemnych, dzielenie - ułamkowych (czyli wymiernych) a pierwiastkowanie - niewymiernych (np. ), które wraz z liczbami wymiernymi stanowią zbiór liczb rzeczywistych.

Operacja pierwiastkowania nie zawsze jest wykonalna w zbiorze liczb rzeczywistych. Zmusza nas to do odpowiedniego rozszerzenia tego zbioru, do zbioru tzw. liczb zespolonych.

Liczby rzeczywiste znajdują swoją interpretację geometryczną w postaci osi liczbowej, czyli w zorientowanej prostej z naniesioną skalą i wskazanym zerem.

Liczb zespolonych szukamy poza osią rzeczywistą. Definiujemy liczbę zespoloną jako parę liczb rzeczywistych

,

tak więc geometryczną ilustracją tego zbioru może być płaszczyzna, na którą naniesiono układ współrzędnych złożony z dwóch prostopadłych osi.

Liczbę nazywamy częścią rzeczywistą a liczbę częścią urojoną liczby zespolonej
.

Zbiór liczb zespolonych jest rozszerzeniem zbioru liczb rzeczywistych w tym sensie, że liczby zespolone leżące na osi „x” utożsamiamy ze zwykłymi liczbami rzeczywistymi. Tak więc oś „x” traktujemy jako zbiór liczb rzeczywistych.

W zbiorze liczb zespolonych wprowadzamy działania (dodawanie i mnożenie). Skoro jednak działania te są już określone w zbiorze liczb rzeczywistych, stanowiących podzbiór liczb zespolonych, to musimy wprowadzić je w taki sposób, aby były z nimi zgodne.

1. Dodawanie

Suma dwóch liczb zespolonych i jest liczbą zespoloną

,

przy czym

,

.

ZADANIE

• Proszę sprawdzić że tak określone dodawanie w zbiorze liczb zespolonych jest zgodne z dodawaniem w zbiorze liczb rzeczywistych.

• Proszę sprawdzić, że dodawanie liczb zespolonych jest przemienne i łączne, czyli że

.

2. Mnożenie

Iloczyn dwóch liczb zespolonych i jest liczbą zespoloną , przy czym

,

.

ZADANIE

• Proszę sprawdzić że tak określone mnożenie w zbiorze liczb zespolonych jest zgodne z mnożeniem w zbiorze liczb rzeczywistych.

• Proszę sprawdzić, że mnożenie liczb zespolonych jest przemienne i łączne, a także, że jest rozdzielne względem dodawania, czyli że

.

ZADANIE

Proszę udowodnić, że mnożenie liczby zespolonej przez liczbę rzeczywistą (traktowaną formalnie jako liczba zespolona) sprowadza się do pomnożenia części rzeczywistej i urojonej przez .

Wartość bezwzględna i argument liczby zespolonej

Płaszczyzna, jako obiekt dwuwymiarowy, może być na nieskończenie wiele sposobów sparametryzowana dwoma liczbami rzeczywistymi. Jednej z tych parametryzacji (kartezjańskiej) już używaliśmy.

Jak wiemy, na płaszczyźnie używa się też współrzędnych biegunowych. Współrzędne te - jak się niżej okaże -wygodne są dla opisu liczb zespolonych.

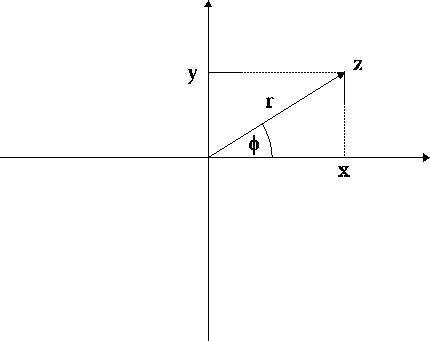
Punkt, który na wstępie opisaliśmy współrzędnymi kartezjańskimi , , możemy też zlokalizować jednoznacznie, podając jego współrzędne biegunowe , przy czym

, .

Współrzędną nazywamy wartością bezwzględną liczby zespolonej (czasami - modułem liczby zespolonej i często zapisujemy ), zaś kąt nazywamy argumentem (fazą) liczby zespolonej.

ZADANIE

Proszę udowodnić, że mnożenie liczb zespolonych polega na pomnożeniu ich wartości bezwzględnych i dodaniu argumentów.

1

---