POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI	Sprawozdanie z ćwiczenia nr 8
	TEMAT: Wyznaczanie momentu bezwładności i sprawdzanie twierdzenia Steinera.
Wydział: PPT Rok: 2	DATA: 21.12.1994 OCENA:

Cel ćwiczenia:

- Stwierdzenie zależności okresu drgań wahadła od momentu bezwładności.

- Doświadczalne potwierdzenie twierdzenia Steinera.

- Wyznaczenie momentu bezwładności ciał względem osi przechodzącej przez

środek masy (tzw. osi środkowej).

Część teoretyczna.

Ruchem drgającym nazywamy każdy ruch lub zmianę stanu, które charakteryzuje powtarzalność w czasie wartości wielkości fizycznych, określających ten ruch lub stan. Jeżeli wartości wielkości fizycznych zmieniające się podczas drgań powtarzają się w równych odstępach czasu to ruch taki nazywamy ruchem okresowym.

Najprostszy rodzaj drgań okresowych są drgania harmoniczne.

Okresem drgań harmonicznych nazywamy najmniejszy odstęp czasu, po upływie którego powtarzają się wartości wszystkich wielkości fizycznych charakteryzujących drganie.

Jako przykład drgań harmonicznych można podać niewielkie wahania wahadła fizycznego.

Wahadło fizyczne jest to ciało doskonale sztywne, które pod wpływem własnego ciężaru waha się dookoła osi nie przechodzącej przez środek ciężkości ciała.

Okres drgań harmonicznych [T] wahadła fizycznego można wyznaczyć korzystając ze związku:

i stąd:

.

Okres drgań harmonicznych nie zależy od kąta wychylenia z położenia równowagi (izochronizm wahań).

Twierdzenie Steinera.

Po przekształceniu wzoru na okres drgań (w/w) otrzymujemy następujące wyrażenie na moment bezwładności:

.

Moment ten jest mierzony względem osi obrotu wahadła.

W praktyce często przydatna jest znajomość momentów bezwładności mierzonych względem osi przechodzącej przez środki ciężkości tych ciał.

Do wyznaczenia momentu bezwładności ciała
względem osi przechodzącej przez środek masy ciała korzysta się z twierdzenia Steinera, które brzmi następująco: różnica momentów bezwładności ciała względem dwu równoległych osi, z których jedna przechodzi przez środek masy, równa jest iloczynowi masy ciała m i kwadratu odległości d między osiami:

.

Dla dwu różnych odległości
i
od osi przechodzącej przez środek masy ciała mamy:

.

Po podstawieniu poprzedniego wzoru otrzymujemy:

.

Otrzymana doświadczalnie stała wartość powyższych wyrażeń może służyć jako potwierdzenie twierdzenia Steinera.

Stała C pozwala obliczyć moment bezwładności ciała względem osi przechodzącej przez środek masy:

.

Urządzenie pomiarowe.

Częścią zasadniczą jest tarcza metalowa z symetrycznie naciętymi otworami. Umieszczenie podpory w postaci metalowej pryzmy w różnych otworach pozwala zmieniać odległości osi obrotu od środka masy tarczy. W drugiej części ćwiczenia rolę wahadła spełnia pierścień metalowy, dla którego daje się zrealizować tylko jedno położenie osi obrotu względem środka masy.

Odległość 2d mierzymy za pomocą suwmiarki.

Okres drgań wyznaczamy za pomocą stopera.

Masę ciała wyznaczamy za pomocą wagi laboratoryjnej.

Część doświadczalno - obliczeniowa.

1. TARCZA.

1. 2d = 149,5mm 0,1mm

d = 74,75mm = 0,07475m 0,0001m

POMIAR	100T [s]	100T	C [ ]	C [ ]
1	68,9	0,0
2	68,8	0,1
3	69,0	0,1
średnia	68,9	0.1	0,1275	0,00190

T = 0,689s 0,001s

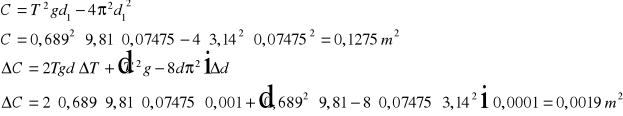
2. 2d = 129,5mm 0,1mm

d = 64,75mm = 0,06475m 0,0001m

POMIAR	100T [s]	100T [s]	C [ ]	C [ ]
1	69,8	0,4
2	69,4	0,0
3	69,0	0,4
średnia	69,4	0,4	0,1404	0,000842

3. 2d = 139,2mm 0,1mm

d = 69,6mm = 0,0696m 0,0001m

POMIAR	100T [s]	T [s]	C [ ]	C [ ]
1	68,0	0,4
2	68,6	0,2
3	68,6	0,2
średnia	68,4	0,27	0,1282	0,000843

4. 2d = 118,5mm 0,1mm

d = 59,25mm = 0,05925m 0,0001m

POMIAR	100T [s]	T [s]	C [ ]	T [ ]
1	68,0	0,2
2	68,2	0,0
3	68,4	0,2
średnia	68,2	0,2	0,1318	0,000782

5. Pomiar masy tarczy.

m = 1,062 kg

m = 1g = 0,001 kg

6. Wyznaczenie średniej wartości C:

POMIAR	C [ ]	C [ ]
1	0,1275	0,001900
2	0,1404	0,000842
3	0,1282	0,000843
4	0,1318	0,000782
ŚREDNIA	0,1320	0,001092

Moment bezwładności
względem środka masy krążka obliczono ze wzoru:

Błąd bezwzględny obliczono ze wzoru:

11. PIERŚCIEŃ METALOWY.

1. 2d = 105mm 0,1mm

d = 52,5mm = 0,0525m 0,0001m

POMIAR	100T [s]	100T [s]
1	67,6	0,2
2	67,3	0,1
3	67,3	0,1
średnia	67,4	0,13

T = 0,674s 0,0013

2. Masa pierścienia.

m = 215,8g = 0,216kg

m = 1g = 0,001kg

3. Moment bezwładności pierścienia I :

I = 0,00128
.

Błąd bezwzględny:

I = 0,000014
.

4. Moment bezwładności względem środka masy (z twierdzenia Steinera):

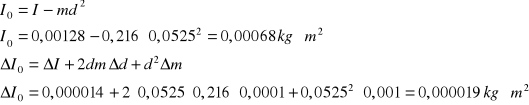
5. Obliczenie momentu bezwładności pierścienia względem środka masy ze wzoru tablicowego:

,

gdzie:

r - promień wewnętrzny : 0,0525m,

R - promień zewnętrzny : 0,0625m.

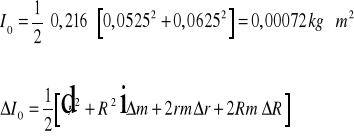
I = 0,0000058
.

111. PORÓWNANIE WYNIKÓW OBLICZEŃ
DLA PIERŚCIENIA METALOWEGO :

METODA			[]
Z twierdz. Steinera	0,00068	0,000019	3,6
Ze wzoru tablicowego	0,00072	0,0000058	0,8

oBardziej dokładny wynik uzyskano w wyniku podstawienia danych do wzoru tablicowego.

Różnica wyników obu metod wynosi 0,00004
.

Wynik ten zawiera się w przedziale błędu wyniku otrzymanego z twierdzenia Steinera (także przy pomocy stałej C).

Wnioski.

Na dokładność pomiarów w przypadku stałej C miały wpływ takie czynniki jak:

- pomiar odległości d (niedokładność związana z odczytem podziałki suwmiarki),

- pomiar okresu drgań T na który wpływ miała chwila uruchomienia i zatrzymania stopera,

a także dokładność odczytu jego wskazań,

Na dokładność pomiaru I i I0 miał dodatkowo wpływ błąd związany z pomiarem masy tarczy.

W przypadku I0 dla metalowego pierścienia okazało się, że dokładniejsze wyliczenie było ze wzoru tablicowego.

6

---