Wydział Mechaniczny

Sprawozdanie z zajęć laboratoryjnych

FIZYKA

Ćwiczenie numer: M-20

Temat: Obliczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego i rewersyjnego.

KAMIL GRYGORUK

Mechanika i Budowa Maszyn

Studia niestacjonarne

Semestr III

Grupa laboratoryjna 2

1. Wprowadzenie:

a) Wahadło matematyczne jest to punkt materialny posiadający pewną masę, zawieszony na nierozciągliwej , nieważkiej nici o długości l. Dla niewielkich odchyleń od pionu (4-5⁰) drgania wahadła matematycznego z bardzo dobrym przybliżeniem możemy uważać za drgania harmoniczne. Przy takim założeniu okres drgań T wahadła nie będzie zależał od amplitudy drgań. Dla wahadła matematycznego okres drgań nie zależy również od masy i wyraża się wzorem:

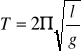
b) Wahadło rewersyjne jest wahadłem fizycznym w konstrukcji którego zostały uwzględnione dwa punkty zawieszenia, których położenia względem środka ciężkości mogą być dowolnie zmieniane. Okres drgań wahadła wyraża się wzorem:

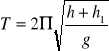
2. Cel i zakres ćwiczenia:

Celem ćwiczenia jest zapoznanie się z problematyką drgań harmonicznych na przykładzie wahadła uniwersalnego (matematycznego i rewersyjnego). Ćwiczenie swoim zakresem obejmuje wyznaczenie przyśpieszenia ziemskiego dwiema metodami, tj. poprzez bezpośredni pomiar okresów drgań wahadeł: matematycznego i rewersyjnego.

3. Pomiary i obliczenia dla wahadła matematycznego:

a) zestawienie wyników pomiarów

t [s]	T [s]	l [mm]	g [m/s^2]
22,955	1,4288	507
22,999	1,4388	507
22,966	1,4399	507
22,966	1,4499	507
22,988	1,4577	507

Wszystkie pomiary wykonywane dla n=16.

b) szacowanie błędów pomiarów

Błędy systematyczne wynikające z dokładności przyrządu:

[s]

[m]

Błąd pomiaru złożonego:

[s]

Błąd złożony
wyraża się wzorem:

c) obliczanie przyspieszenia ziemskiego z uwzględnieniem błędów

Według obliczeń średni błąd wynosi:

zatem wartość przyspieszenia ziemskiego wyznaczonego w wyniku pomiarów wynosi:

4. Pomiary i obliczenia dla wahadła rewersyjnego:

a) zestawienie wyników pomiarów

t1	T1	t2	T2		l [m]	g

Wszystkie pomiary wykonywane dla n=6.

b) szacowanie błędów pomiarów

Błędy systematyczne wynikające z dokładności przyrządu:

[s]

[m]

Błąd pomiaru złożonego:

[s]

Błąd złożony
wyraża się wzorem:

c) obliczanie przyspieszenia ziemskiego z uwzględnieniem błędów

Według obliczeń średni błąd wynosi:

zatem wartość przyspieszenia ziemskiego wyznaczonego w wyniku pomiarów wynosi:

5. Wnioski:

W obu przypadkach otrzymaliśmy bardzo zbliżone do siebie wartości. Dla wahadła matematycznego g = 9,7482
0,2745 [m/s²], zaś dla rewersyjnego g = 9,728
0,314 [m/s²]. Rzeczywista wartość przyspieszenia ziemskiego wynosi g = 9,8066 [m/s²], zatem wynik pomiaru mieści się w granicy błędu.

---