EAIiE |
Krzysztof Jasek Piotr Jóźwik |
rok I |
grupa III |
zespół 12 |
|
Pracownia fizyczna I |
Przenikalność dielektryczna |
ćwiczenie 33 |
|||
data wykonania
23.03.2001 |
data oddania
30.03.2001 |
zwrot do popr. |
data oddania |
data zaliczenia |
ocena |
Cel ćwiczenia.
Wyznaczanie przenikalności dielektrycznej próżni ε0 i przenikalności względnych εr różnych materiałów poprzez pomiar pojemności kondensatorów powietrznych i z warstwą dielektryka.
Wprowadzenie.
Kondensator jest układem przewodników oddzielonych warstwą izolatora. Pojemność kondensatora C definiujemy jako stosunek ładunku Q zgromadzonego na okładkach do napięcia U miedzy okładkami.
Z prawa Gaussa można wyprowadzić wzór na pojemność kondensatora płaskiego:
![]()
gdzie S - powierzchnia okładki, d- odległość między okładkami,
εo - przenikalność dielektryczna próżni
εr - względna przenikalność dielektryczna materiału pomiędzy okładkami kondensatora
Wyznaczanie przenikalności dielektrycznej próżni:
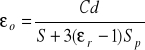
Do eksperymentu posłużymy się kondensatorem powietrznym, który będzie przybliżeniem próżniowego. Okładki stanowią dwie okrągłe płyty metalowe. Określoną odległość między płytami uzyskuje się przez umieszczenie w trzech miejscach stosu izolujących krążków. Do pomiaru pojemności kondensatora stosujemy cyfrowy miernik pojemności. Błąd wyznaczanej pojemności wynosić będzie zatem 1% wartości mierzonej +0,1% zakresu. Pojemność takiego kondensatora wynosić będzie:
gdzie εr - pojemność materiału przekładek, Sp - powierzchnia okładek.
W ćwiczeniu zastosujemy doświadczalny sposób eliminacji wpływu pola rozproszonego. Efektywna „objętość” pola rozproszonego jest rzędu 2πrd2 gdyż pole to zajmuje z grubsza pas wysoki i szeroki na d wokół obwodu kołowych płyt kondensatora. Objętość pola jednorodnego w kondensatorze wynosi πr2d. Względny udział pola rozproszonego maleje więc do zera w granicy przy d zmierzającym do zera.
Wykonamy zatem serię pomiarów pojemności C dla różnych wartości d, a następnie wykres iloczynu Cd w funkcji grubości d.
Przez uzyskane punkty poprowadzimy gładką krzywą i ekstrapolujemy ją do wartości d=0. Ekstrapolowaną wartość Cd podstawiamy do wzoru na przenikalność.
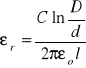
Obok kondensatora płaskiego przykładem obiektu o określonej pojemności jest kabel koncentryczny. Można go traktować jako kondensator cylindryczny, którego jedną okładką jest środkowy drut, drugą - oplot. Pojemność takiego kondensatora wyraża wzór:
w którym R i r oznaczają promienie okładek kondensatora, l jest jego długością.
Pośrednie wyznaczanie prędkości światła w próżni:
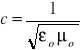
Ponieważ pełny układ równań elektromagnetycznych wiąże ze sobą stałe przenikalności magnetycznej i dielektrycznej wymagają one w próżni tylko jednej stałej doświadczalnej. Wartość stałej μo=4π*10-7 Vs/Am. Dodatkowo stałe te są związane z prędkością światła w próżni zależnością:
Pomiar przenikalności dielektrycznej próżni stanowi więc pośrednią metodę wyznaczenia prędkości światła.
![]()
Wyniki pomiarów i obliczenia:
Pomiary dla przekładek.
Wyniki pomiarów zostały umieszczone w tabelach, oraz na dołączonym wykresie Cd(d). Z wyznaczonych punktów wykresu można ekstrapolować wartość Cd dla d=0. Wartość ta będzie odpowiadała sytuacji, kiedy stosunek pola zewnętrznego do wewnętrznego wynosi zero. Błąd takiej ekstrapolacji przyjmujemy równy odchyłce pierwszego punktu pomiarowego, który ma największy wpływ na wartość ekstrapolowaną.
(tabele przekładek, wykresCd)
Błąd obliczonej wartości przenikalności dielektrycznej obliczamy z wzoru na przenoszenie błędów:
(wzór)
traktując C*d jako jedną zmienną, której odchyłkę obliczamy ze wzoru:
(odchyłka Cd)
Ostatecznie wyznaczona przez nas wartość przenikalności dielektrycznej próżni(powietrza) wynosi εo= obarczona błędem Δεo=
Wyznaczanie względnej przenikalności wybranych dielektryków.
Pomiary pojemności dla kondensatora z umieszczonymi wewnątrz cienkimi płytkami zostały umieszczone w tabelach. Pomiar grubości płytek powtórzyliśmy dziesięciokrotnie, aby otrzymać dokładniejszy wynik.
Względną przenikalność obliczymy z wzoru:
![]()
Odchyłkę Δεr obliczamy stosując metodę przenoszenia błędów.
Wyznaczanie wartości względnej przenikalności dielektrycznej materiału użytego do wyrobu kabla koncentrycznego.
Wzór przenikalność względną kondensatora cylindrycznego, którego przykładem jest kabel koncentryczny:
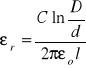
Odchyłkę Δεr wyznaczamy z wzoru na przenoszenie błędu.
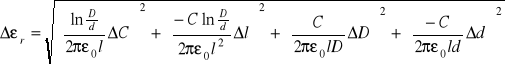
Wyniki pomiarów oraz obliczeń umieściliśmy w tabeli
(tabela-koncentryki)
Na podstawie otrzymanych wyników można wysnuć wniosek, iż badane kable koncentryczne były jednego typu oprócz jednego, wyraźnie odstającego wynikami od reszty.
Wyznaczanie prędkości światła.
Na podstawie wyznaczonej przez nas wartości przenikalności dielektrycznej próżni oraz definicji przenikalności magnetycznej próżni można wyznaczyć prędkość światła z wzoru:
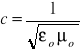
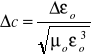
Błąd wyznaczonej stałej c obliczamy z prawa przenoszenia błędu.
Obliczona przez nas wartość c= obarczona błędem równym Δc=
Wnioski:
Wyniki przeprowadzonych przez nas doświadczeń zgadzają się w granicach błędów z wartościami tablicowymi. Największy przyczynek do błędu przenikalności próżni wnosi przyjęta przez nas ekstrapolacja, która wskutek braku danych na temat krzywej interpolowanej jest bardzo niedokładna.
Przy wyznaczaniu przenikalności względnej duży wpływ na jakość pomiarów miało niewątpliwie zużycie płytki, która wielokrotnie mierzona nieostrożny sposób śrubą mikrometryczną (zapewne bez użycie sprzęgiełka) była poprzecierana i nierówna.
Przybliżenie próżni powietrzem w tym przypadku daje zaniedbywalne odchylenie z uwagi na bardzo bliską jedności względnej przenikalności dielektrycznej dla powietrza.
Pomiar εr dla kabli koncentrycznych jest obarczony błędem najprawdopodobniej wynikającym z dużej plastyczności materiału dielektryka wewnątrz kabla a co za tym idzie, problematycznym pomiarze średnicy (materiał ulegał odkształceniom nawet przy użyciu sprzęgiełka przy śrubie mikrometrycznej). Problemem także okazało się poprawne zmierzenie długości kabla, ponieważ był pogięty i nierówny nawet po rozprostowaniu do pomiaru.
![]()
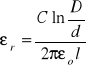
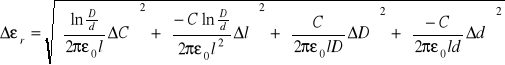
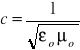
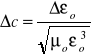
![]()
![]()
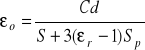
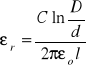
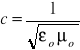
Wyszukiwarka
Podobne podstrony:
4241
4241
4241
4241
4241
4241
4241
4241
03 Istota STWid 4241 (2)
4241
akumulator do astra hd 8 4241 4241 t 4244 4244 t 4248 4248
więcej podobnych podstron