W Y K Ł A D 1
POJĘCIA PODSTAWOWE
Wprowadzenie
Oznaczenia
Wielkości fizyczne jako funkcje czasu t, zazwyczaj oznacza się małymi literami np.:
napięcie u lub u(t); prąd i lub i(t); ładunek q lub q(t); potencjał * lub *(t), i.t.d.
Dużymi literami oznacza się zazwyczaj wielkości stałe w czasie np.:
napięcie stałe U, prąd stały I, ładunek stały Q, potencjał stały V, i.t.d.
Mogą istnieć odstępstwa, np. * = *(t). dla stałego jak i zmiennego w czasie.
Wielkości wektorowe: E, H, D, B, F.
Wymiar i jednostki: Stosowanym układem jednostek jest układ SI.
Sygnały
Funkcje opisujące zmienności w czasie wielkości fizycznych nazywa się przebiegami czasowymi tych wielkości lub sygnałami.
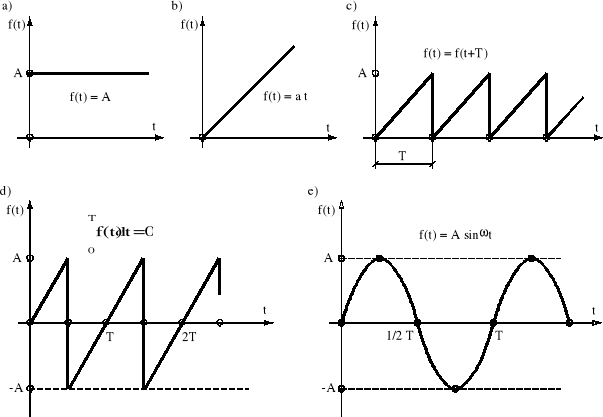
Rys.1.1. Rodzaje sygnałów: a) - stały, b) - zmienny, c) - okresowy, d) - przemienny, e) - sinusoidalny
Dziedziną sygnałów jest :
przedział czasu 0 ≤ t < +∞ lub 0 < t < +∞ dla zjawisk rozpoczynających się w chwili początkowej t = 0,
-∞ < t < +∞ dla zjawisk trwających dostatecznie długo od chwili początkowej tak, że można je uważać za nie mające swojego początku w czasie.
1.2. Potencjał elektryczny
![]()
, (1.1)
gdzie siła F określona jest prawem Coulomba
![]()
, (1.2)
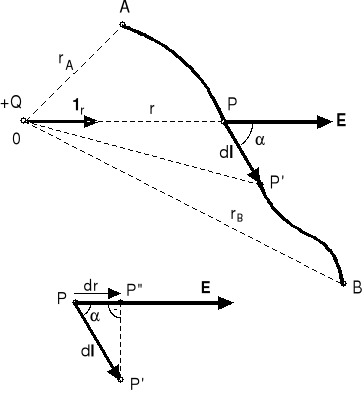
Rys.1.2. Przemieszczanie ładunku q wzdłuż krzywej AB w polu elektrycznym ładunku punktowego Q
gdzie: 1r jest wektorem jednostkowym, ε = εr ε0 ε0 = 8,856 ⋅ 10-12 F/m
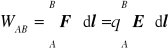
. (1.3)
![]()
(1.4)
![]()
, (1.5) 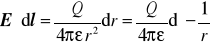
. (1.6)
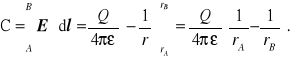
(1.7)
Cyrkulacja pola E wzdłuż AB jest różnicą wartości pewnej funkcji skalarnej V(x,y) odpowiednio w punkcie A i B, czyli różnicą między V(A) i V(B):
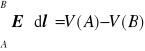
. (1.8)
Tę funkcję skalarną nazywa się potencjałem
![]()
. (1.9) ![]()
. (1.10)
![]()
. (1.11)
Jeżeli rB → ∞, to praca
![]()
. (1.12) ![]()
(1.13)
Potencjałem elektrycznym w punkcie A pola elektrycznego nazywa się stosunek pracy wykonanej przy przemieszczaniu ładunku „próbnego” q z punktu A do nieskończoności, do ładunku „próbnego” q.
Różnicę potencjałów we wzorze (1.11) nazywa się napięciem elektrycznym między dwoma punktami A i B
UAB = V(A) - V(B) . (1.14)
Napięciem elektrycznym między dwoma punktami A i B pola elektrycznego nazywa się stosunek pracy, jaką wykonałyby siły pola elektrycznego przy przemieszczaniu ładunku „próbnego” dodatniego q z punktu A do punktu B do ładunku „próbnego” q.
Jednostką potencjału i napięcia elektrycznego jest 1 wolt (1 V). Jeżeli uwzględni się wzór (1.8), to jednostką natężenia pola elektrycznego E jest wolt na metr (V⋅m-1).
WAB = q U (1.15)
i jest ona równa zeru, jeżeli przemieszczenie to odbywa się wzdłuż krzywej zamkniętej (punkt A pokrywa się z punktem B), gdyż
![]()
(1.16)
Jest to jedna z podstawowych własności pola elektrycznego - pole elektryczne jest polem potencjalnym.
Potencjał elektryczny V jest ściśle związany z wektorem natężenia pola elektrycznego E.
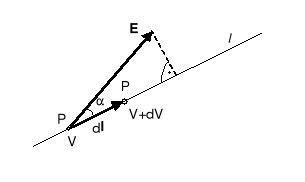
![]()
. (1.17)
![]()
, (1.18)
gdzie: El jest rzutem prostokątnym wektora E na prostą l. Stąd otrzymuje się:
Rys.1.3. Potencjał elektryczny V i natężenie
pola E wzdłuż prostej l
![]()
. (1.19)
Wynika stąd, że wektor El jest skierowany w kierunku malejącego potencjału, a jego wartość zależy od „szybkości” zmiany potencjału wzdłuż prostej l.
![]()
![]()
![]()
. (1.20)
zaś wektor
E = Ex 1x + Ey 1x + Ez 1z . (1.21) E = - grad V(x, y, z) = - ∇V(x, y, z) . (1.22)
Pole to jest jednoznacznie określone i można je wyznaczyć, jeżeli dany jest rozkład potencjału V(x, y, z) w rozpatrywanej przestrzeni. W zagadnieniu odwrotnym
![]()
. (1.23)
Na podstawie wzoru (1.23) potencjał V(x, y, z) oblicza się z dokładnością do stałej całkowania. Wyznaczenie tej stałej, a zatem i potencjału, wymaga przyjęcia potencjału odniesienia w wybranym punkcie rozważanego obszaru. Potencjały w pozostałych punktach będą odniesione do potencjału wybranego punktu, będą zatem faktycznie różnicami potencjałów (napięciami) między tymi punktami a punktem odniesienia.
Prąd elektryczny, natężenie prądu, gęstość prądu
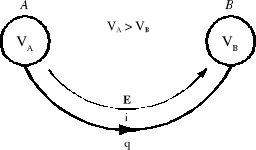
Rys.1.4. Przepływ prądu elektrycznego
Prądem elektrycznym rozpatrywanym jako zjawisko fizyczne nazywamy uporządkowany ruch ładunków elektrycznych przez rozpatrywany przekrój poprzeczny środowiska na skutek działania pola elektrycznego o natężeniu E.
Prądem elektrycznym nazywamy wielkość skalarną zdefiniowaną jako granica stosunku ładunku elektrycznego Δq (przepływającego przez dowolny przekrój obwodu prądowego) do czasu Δt (w którym odbył się ten przepływ).
![]()
. (1.24) ![]()
. (1.25)
Jednostką natężenia prądu elektrycznego w układzie SI jest 1 amper (1 A).
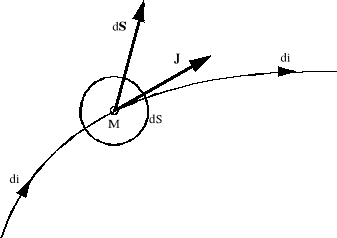
Rys. 1.5. Wektor gęstości prądu
Prawo Ohma w postaci różniczkowej
![]()
, (1.29) prawo Ohma ![]()
, (1.30)
konduktywnością (przewodność właściwa) { [*] = 1 S·m-1 = 1 Ω-1·m-1 }:
![]()
(1.31)
rezystywnością (oporność właściwa) { [*] = 1 Ω·m }:
![]()
(1.32)
Elementy obwodu elektrycznego
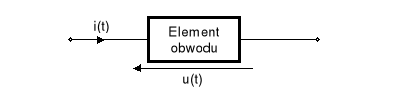
Rys.1.6. Symbol graficzny elementu obwodu
Jeżeli ładunek d q(t) przemieszcza się z punktu A do punktu B , to
![]()
, (1.35) ![]()
, (1.36) ![]()
. (1.37)
Jednostką energii jest joul; [w] = 1 V∙A∙s = 1 W∙s = 1 J.
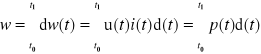
, (1.38)
gdzie moc chwilowa
![]()
, (1.39) ![]()
. (1.40)
Jednostką mocy jest wat; [p] = 1 V∙A = 1 W.
Jeżeli w > 0, oznacza to, że w przedziale czasu <t0, t1 > element faktycznie pobrał energię z „otoczenia”. Jeśli wartość ta jest ujemna, świadczy to o tym, że element faktycznie oddał do „otoczenia” energię równą:
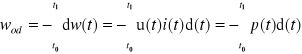
. (1.41)
W wielu przypadkach rozważa się energię pobraną w przedziale czasu < t0, t >, gdzie t > t0 jest chwilą bieżącą. Wówczas w(t0 , t) jest funkcją górnej granicy całkowania:
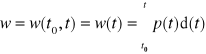
. (1.42)
Dla prądu stałego u(t) = U oraz i(t) = I i wtedy (t0 = 0) energia
![]()
, (1.43) oraz moc ![]()
. (1.44)
Elementy obwodów elektrycznych dzielimy dalej na elementy pasywne, czyli elementy, które posiadają zdolność akumulacji energii (kondensator C, induktor L) lub elementy rozpraszające energię (rezystor R).
Element przedstawiony na rys.1.6 będzie pasywny, gdy spełniona zostanie zależność:
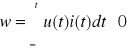
. (1.45)
Rezystor jest elementem pasywnym, gdyż energia określona wzorem (1.45)
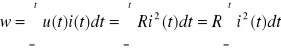
> 0 . (1.46)
Element obwodu elektrycznego, dla którego energia określona wzorem (1.67) przyjmuje wartości ujemne, jest elementem aktywnym. Zatem każdy element aktywny wykazuje zdolność dostarczania energii elektrycznej. Elementy takie nazywamy elementami aktywnymi źródłowymi lub krótko źródłami.
Źródła dzielimy na źródła autonomiczne (niesterowane) i na źródła sterowane.
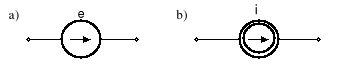
Rys.1.7. Symbole graficzne źródeł autonomicznych: a) idealne źródło napięcia; b) idealne źródło prądu
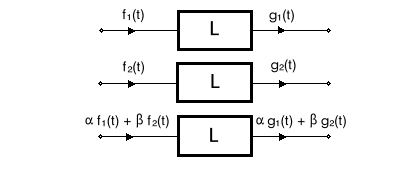
Rys.1.8. Interpretacja liniowości elementu
Jeżeli na wymuszenie f1(t) uzyskujemy odpowiedź elementu w postaci g1(t), a na wymuszenie f2(t) odpowiedź g2(t), oraz gdy na dowolną kombinację liniową wymuszeń uzyskuje się liniową kombinację odpowiedzi, to element L jest liniowy.
Element, który nie spełnia zasady opisanej wzorem (1.47), jest elementem nieliniowym.
Element obwodu elektrycznego nazywamy stacjonarnym, jeżeli nie zmienia swych właściwości w czasie, tzn. jeżeli na wymuszenie f1(t) występuje odpowiedź g1(t), to na wymuszenie f1(t ± τ) występuje odpowiedź g1(t ± τ) dla każdej wartości τ.
Element, w którym na dowolne wymuszenie f(t) występuje odpowiedź g(t), niezależna od współrzędnej przestrzennej a zależna jedynie od czasu, nazywamy elementem skupionym (dyskretnym).
Element obwodu elektrycznego nazywamy odwracalnym, jeżeli ma takie same właściwości niezależne od sposobu połączenia elementu w obwodzie i niezależne od biegunowości przyłożonego napięcia (np. rezystor).
Element mający dwa wyróżnione zaciski nazywamy dwójnikiem. Element o większej liczbie zacisków nazywamy wielobiegunnikiem lub elementem wielozaciskowym.
Obwód elektryczny
Obwodem elektrycznym nazywamy zespół elementów połączonych ze sobą w taki sposób, że istnieje co najmniej jedna droga zamknięta do przepływu prądu.
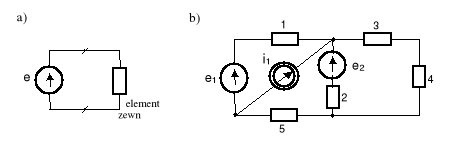
Rys.1.9. Schemat obwodów elektrycznych: a) obwód prosty (jednooczkowy); b) obwód złożony
Oczkiem obwodu elektrycznego nazywamy kontur, który jest zbiorem połączonych ze sobą gałęzi tworzących drogę zamkniętą dla przepływu prądu, a mający tę własność, że usunięcie dowolnej gałęzi ze zbioru powoduje, że pozostałe gałęzie nie tworzą już drogi zamkniętej.
Przykładowymi oczkami dla rys.1.9b może być zbiór gałęzi (O1 = {e1, 1, i1}; O2 = {2, e2, 3, 4}; O3 = {5, i1, e2, 2}).
Gałęzią obwodu elektrycznego nazywamy zbiór połączonych ze sobą elementów, przez które płynie ten sam prąd. Wewnątrz może znajdować się dowolna liczba końcówek, ale na zewnątrz wyprowadzone są tylko dwie (rys.1.10).

Rys.1.10. Przykłady gałęzi obwodu elektrycznego
Węzłem obwodu elektrycznego nazywamy zacisk gałęzi, do której są dołączone inne gałęzie.
Tak więc każda gałąź ograniczona jest dwoma węzłami (rys.1.11a i b).
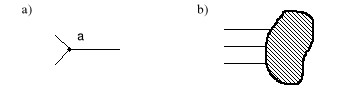
Rys.1.11. Przykłady węzłów obwodu elektrycznego: a) prosty węzeł; b) uogólniony węzeł
. Obwód elektryczny jest obwodem skupionym liniowym stacjonarnym (SLS), jeżeli można go opisać za pomocą liniowych równań algebraicznych lub liniowych równań różniczkowych o stałych współczynnikach.
Prawa Kirchhoffa i zasada Tellegena
Pierwsze prawo Kirchhoffa.
Dla każdego węzła obwodu elektrycznego suma algebraiczna prądów jest równa zeru.
![]()
, (1.48)
gdzie:
1 - gdy prąd k-tej gałęzi skierowany jest do n-tego węzła,
δnk = -1 - gdy prąd k-tej gałęzi skierowany jest od n-tego węzła,
0 - gdy k-ta gałąź nie ma punktu wspólnego z n-tym węzłem .
i1+ i2 - i3 - i4 + i5 = 0 (1.49) lub i1 + i2 + i5 = i3 + i4 . (1.50)
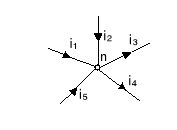
Na podstawie równania (1.50) I prawo Kirchhoffa można również sformułować:
Suma prądów dopływających do węzła jest równa sumie prądów z niego odpływających.
Pierwsze prawo Kirchhoffa można napisać w postaci wektorowej:
Rys.1.12. Przykładowy węzeł obwodu elektrycznego
![]()
. (1.51)
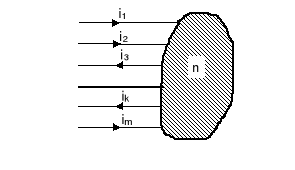
Z równania (1.51) wynika, że w polu przepływowym strumień wektora gęstości prądu przepływającego przez dowolną powierzchnię zamkniętą jest równy zeru.
![]()
. (1.52)
Rys.1.13. Uogólniony węzeł
Drugie prawo Kirchhoffa.
W dowolnym oczku obwodu elektrycznego, przy dowolnym charakterze zmienności na-pięć, suma algebraiczna wartości chwilowych napięć źródłowych występujących w oczku i napięć odbiornikowych jest równa zeru.
Suma algebraiczna napięć źródłowych jest równa algebraicznej sumie napięć odbiornikowych.
![]()
, (1.53)
gdzie:
{
1 - gdy kierunek (zwrot) napięcia odbiornikowego uk zgodny jest z przyjętą
δnk =
orientacją n-tego oczka,
-1 - gdy kierunek (zwrot) napięcia odbiornikowego uk przeciwny jest przyjętej
orientacji n-tego oczka.
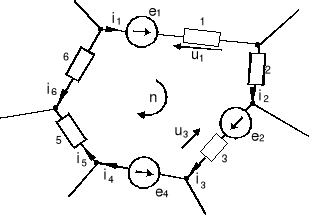
Rys.1.14. Przykładowe oczko obwodu elektrycznego
Jeżeli dane są parametry obwodu (schemat obwodu), a poszukuje się napięć prądów w poszczególnych częściach obwodu, to takie zagadnienie nazywamy analizą obwodu. Jeżeli natomiast dane są niektóre napięcia i prądy w określonych częściach obwodu, a poszukuje się schematu i parametrów elementów, to zagadnienie nosi nazwę syntezy obwodu elektrycznego.
Zasada Tellegena.
Dla dowolnego k-tego elementu moc chwilowa ![]()
. (1.55)
W każdym układzie skupionym suma mocy chwilowych pobieranych przez wszystkie elementy układu jest w każdej chwili równa zeru dla każdego czasu t :
![]()
. (1.56)
Zasada Tellegena wyraża zasadę zachowania mocy w odniesieniu do układu skupionego.
Z powyższego wzoru wynika, że w każdej chwili w układzie elementy faktycznie pobierają moc ( pk (t) > 0 ) , inne ją oddają ( pk (t) < 0 ) , oraz że
Suma mocy pobieranych przez elementy układu skupionego jest w każdej chwili równa sumie mocy oddawanych przez pozostałe elementy układu.
![]()
![]()
. (1.57)
W dowolnym przedziale czasu < t0, t1 > suma energii pobranych przez elementy układy skupionego jest równa sumie energii oddanych przez pozostałe elementy.
Zasada Tellegena wyraża zatem zasadę zachowania energii w odniesieniu do układu skupionego.
1
9
![]()
. (1.26)
![]()
(1.27)![]()
. (1.28)
Jednostką gęstości prądu jest 1 amper na metr kwadratowy (1A∙m-2).
u = f(i) (1.33)
i = F(u). (1.34)
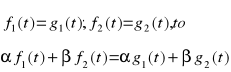
(1.47)
dla dowolnych wartości α i β ze zbioru liczb rzeczywistych (α,β ∈ R).
![]()
. (1.54)
Całka z wektora natężenia pola po drodze zamkniętej jest równa zeru.
Wyszukiwarka
Podobne podstrony:
ET-1 progr., ►Studia, Semestr 2, Elektrotechnika wykład
W-7 w w, ►Studia, Semestr 2, Elektrotechnika wykład
Zal Egz, ►Studia, Semestr 2, Elektrotechnika wykład
El en i środowisko 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Narazenia od pól elektromagnetycznych 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład
Narazenia od pól elektromagnetycznych 13 14 2, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład
Moc bierna 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
ET 2 mgr program 05 06, ►Studia, Semestr 3, Ekektrotechnika wykład
Elektrownie wiatrowe 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
13 14 Seria 1.2, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Duże odstępy powietrzne 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
13 14 Seria 1.3, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Składowe symetryczne, ►Studia, Semestr 4, Elektrotechnika instrukcje
Elektrownie cieplne 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Elektrownie cieplne 13 14 2, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Straty energii 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Obwody sprzężone magnetycznie, ►Studia, Semestr 3, Elektrotechnika Laboratorium, Instrukcje
Obci-¬enie okresowe 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Poprawa współczynnika mocy, ►Studia, Semestr 3, Elektrotechnika Laboratorium
więcej podobnych podstron